【多目标进化优化】 MOEA 测试函数

声明

本文内容来源于 《多目标进化优化》 郑金华 邹娟著，非常感谢两位老师的知识分享，如有侵权，本人立即删除，同时在此表示，本文内容仅学习使用，禁止侵权，谢谢！

注：本文中提到的参数与（决策）变量为同一概念，不作区分；参数向量与决策向量两个概念不作区分

1. 概述

\quad\quad 测试多目标进化算法的目的是对算法进行评估、比较或分类，以提高算法性能，即提高 MOEA 求解问题的效果和效率。关于 MOEA 的测试，首先应当明确几个问题。

\quad\quad ① MOEA 测试具体内容是什么？ 一般说来，多目标优化问题的一个测试函数或一组测试函数，或一个实际应用问题可以构成对 MOEA 的测试。

\quad\quad ② 怎样找到一个合适的 MOEA 测试函数？可以从已有的 MOEA 文献，或者他人提出和总结的构造测试函数的方法，或者为人熟知的实际应用问题中找到一个合适的 MOEA 测试。

\quad\quad ③ 何时对 MOEA 进行测试？可以在一个 MOEA 的设计与实现过程中不断地对它进行测试，也可以在一个 MOEA 完全实现以后再对它进行测试。

\quad\quad ④ 怎样设计一个 MOEA 的测试？ 一般地，一个完整的测试应包括计算平台、统计工具、MOEA 评价工具或方法、实验计划等。

\quad\quad 因此， 在 MOEA 的设计与实现过程中，不仅要投入精力去确定合适的测试，设计合适的 MOEA 实验，还要选取最可靠的测试工具（或方法），同时也必须做好相应的统计评估与比较判断等工作。

\quad\quad 许多 MOEA 研究主要使用数值 MOP 函数来展现、评价 MOEA 的性能。在选择具体的 MOP 时，为什么选择这个（些），而不选择那个（些），依据是什么？因此，为了评价 MOP 选择的合理性，对于 MOP 理论和问题结构的综合讨论是必要的，只有这样才能正确地解释选择这些 MOP 到底是否合适。MOP 的特征包括目标函数的结构、约束的或非约束的基因型和表现型的形式化表示，以及参数对函数图像等的影响等。文献（Deb, 1999； Deb et al, 2001 ； Veldhuizen et al, 1999, 1999a； Zydallis et al, 2001 ； Huband et al, 2006）中讨论了典型的测试函数及其相关的特征，为比较 MOEA 的性能提供了必要的基础。随着 MOEA 研究和应用的不断深入，研究者们相继研发了一些实用的 MOEA 测试工具包

\quad\quad 本文主要讨论测试函数的构造原则与方法、各种 MOP 测试函数的特点，以及几类常用的测试问题集。

2. MOEA 测试函数集

\quad\quad 一些典型的测试函数被广泛地用于 MOEA 的实验，其原因主要有两个：一是其他相关的研究学者采用了这些测试函数，二是这些 MOP 能够测试出 MOEA 某些算子的性能，并且在某种程度上它们比较 “容易” 找到最优解。对于将这些测试函数包含到普遍的、一般的测试函数集中是否合适，在这方面目前还没有很多解释和讨论。Poloni 等指出，“复杂” 的 MOEA 性能评估测试方法比较缺乏 (Poloni etah 1996a)。这就说明，非常有必要寻找合适的测试函数用于评价 MOEA 的性能 (效果和效率)。许多学者同时也注意到了这一点， 并做了相当广泛和深入的研究，如文献(Deb, 1999； Veldhuizen, 1999) 设计和构造了较多 MOEA 测试函数，本章将对几类常用的测试函数进行讨论。

\quad\quad 在某种程度上，可以说测试函数集既是非常有意义的，又是没有什么意义的。因为任意 一个 MOEA，它即使成功地 “通过” 了所有测试函数的测试，也不能保证它能对实际应用问题继续保持其效果和效率。当将 MOP 领域和 MOEA 领域结合起来看时，新的和未知的情况便会使得算法的运行结果不理想。一般地，只有当所有的情况都被考虑的情况下，才可以说一个 MOEA 的测试集是一个有价值的、有意义的工具。为了更好地研究 MOP 测试集，首先来看一看单目标进化算法 (EA) 测试函数。

\quad\quad 单目标测试函数用于检测 EA 求解各种不同特点的问题的能力。测试函数集涵盖了相应的搜索空间的特征。下面给出一些 EA 的单目标测试函数。

\quad\quad ① De Jong 提出了 5个单目标遗传算法 (GA) 优化测试函数(Jong, 1975)： sphere parabolic, Rosenbrock ridge, Rastrigrin steps, Griewank quartic, Schaffer F6 foxholeso

\quad\quad ② Michalewicz 等提出了 12 个单目标带约束的优化测试函数(Michalewicz et al, 1996)。

\quad\quad ③ Schwefel 提出了基于进化策略的分布为 62 种形态 (landscape) 的函数 (Schwefel, 1995)。

\quad\quad ④ Whitley 等 (Whitley et al, 1996) 和 Goldberg 等(Goldberg et al, 1989) 提出了其他规范化 (formal) 的 GA 测试集，YaoXin 等 (Yao X et al, 1996, 1997) 提出了非规范化 (informal) 的 GA 测试集。

\quad\quad ⑤ 欺骗问题，包括 Goldberg 的 order 3 和 6、bipolar order 6、Muhenbein 的 order 5。

\quad\quad ⑥ Digalakis 和 Margaritis 提出了 8 个标准函数和 6 个非线性的二次函数 (Digalakis et al, 2000)。

\quad\quad ⑦ 多个最优值问题：Levy 函数 (Levy et al, 1981)、Corana 函数 (Corana et al, 1987)、Freudenstein-Roth 函数和 Goldstein-Price 函数(More et al, 1981) 。

\quad\quad ⑧ 其他如 Ackley 函数、Wirestrass 函数 (连续的但非处处可微的)。

\quad\quad De Jong 的 5 个 GA 测试函数分别体现了下列性质(Goldberg et al, 1989)：连续的和非连续的、凸的和非凸的、单峰的和多峰的、二次的和非二次的、低维的和高维的、确定性的和随机性的。Michalewicz 等讨论了下列内容 (Michalewicz et al,1996)：目标函数的类型 (如线性的、非线性的、二次的)、决策变量的个数、约束条件及约束条件的类型 (线性的和/或非线性的)、影响函数最优值的约束条件数目，以及可行解区域占整个探索空间的比 例等。

\quad\quad 一般来说，在选择、研究 MOP 时应当考虑下列基本特征：

\quad\quad ① 连续的或非连续的或离散的。

\quad\quad ② 可导的或不可导的。

\quad\quad ③ 凸的或凹的。

\quad\quad ④ 函数的形态(单峰的，多峰的)。

\quad\quad ⑤ 数值函数或包含字母与数字的函数。

\quad\quad ⑥ 二次方的或非二次方的。

\quad\quad ⑦ 约束条件的类型（等式、不等式、线性的、非线性的）。

\quad\quad ⑧ 低维的或高维的（基因型、表现型）。

\quad\quad ⑨ 欺骗问题或非欺骗问题。

\quad\quad ⑩ 相对 $P{F}_{true}$ 有偏好或无偏好。

\quad\quad EA 和 MOEA 的测试函数集应当包含一系列从“易” 到 “难” 的数值优化问题，同时也应当包含反映实际应用问题的函数。

\quad\quad Whitley 等提出了多目标优化/决策问题的测试函数设计准则（Whitley et al, 1996）：

\quad\quad ① 测试问题必须是简单搜索策略所不易解决的

\quad\quad ② 测试函数中应包括非线性耦合以及非对称问题

\quad\quad ③ 测试问题中应包括问题规模可伸缩的问题

\quad\quad ④ 一些测试问题的评估代价应具有可伸缩性

\quad\quad ⑤ 测试问题应有规范的表达形式

\quad\quad Holland 指出，算法对 “某几个” 数值函数的性能表现的好坏，并不能在说明算法对复杂的实际应用问题的性能好坏方面，以及科学地设计和分析实际应用问题方面起到作用 （Holland, 2000）。也就是说，某几个测试函数能够对不同 EA 的性能进行比较，但是通过这样比较而得出的结论并不能说明 EA 求解实际应用问题的能力的强弱。对于 MOEA 来说， 这样的情况也同样存在。因此，应当在充分了解并掌握这一情况的基础上，根据确定的目标来选择 MOP 测试集。

\quad\quad 此外，NFL （no free lunch）定理（Wolpert et al, 1997）指出，如果涉及测试问题领域的知识没有与算法方面的知识相结合，那么就无法保证算法的鲁棒性；同时，如果测试问题领域的知识与算法方面的知识结合得过于紧密，又会降低算法在求解其他类问题甚至同类问题时的有效性，也就是说，算法是非鲁棒性的。因此，在选择 MOP 测试集时还要考虑问题领域的基本特征。只要测试集包含了问题领域的基本的主要特征，那么任意一个搜索算法在求解同类问题时都会保持其效果和效率。综上分析，大部分典型的 MOP 问题领域的显著特征有助于形成一个较完善的 MOP 测试集。

\quad\quad 一个 MOEA 应当在收敛到 Pareto 最优面（$P{F}_{true}$）的同时保持良好的分布度。 如果仅仅在逼近 $P{F}_{true}$ 时再采取保持解的分布度的措施，势必会影响算法的效果。并且，如果 $P{F}_{true}$ 在目标空间中的某些区域内是稀疏的凹的曲线（面）（如离散化的），虽然在这些区域内不要求分布性，但在其他的点密集的可行区域内仍然是要求解的分布性的。某些带约束的问题虽出现为 “空” 的区域，但在其他区域也有分布性的要求。因此，设计测试函数的时候也要考虑 $P{F}_{true}$ （决策空间 Pareto 最优解）和 $P{F}_{true}$ 的分布性对算法的要求。

3. MOP 问题分类

\quad\quad 本节以测试函数的主要特征作为分类的标准，对 MOP 测试函数进行较详细的讨论。

\quad\quad 正如单目标 EA 优化问题，某些 MOP 适合作为一些实际的多目标应用问题的代表。大多数实际应用问题的模型可以用数学函数的结构来描述，但是 MOP 必须获得更多的关于该模型的信息，并以此为依据而产生多个目标函数。对一个实际应用问题进行建模，可以产生数值优化或组合优化 MOP，既可能简单，也可能复杂。一个 MOP 可能包含连续的、离散的或有约束的函数，或这些函数的混合。

\quad\quad 当问题的决策变量呈多维，且单目标搜索空间很大时，EA 对这类问题有着很强的搜索能力。对于多目标优化来说，常用的数值优化函数并没有清晰、明确地反映出多维变量的问题特征。在本书 附录 B 中列出了 30个不同的数值优化 MOP，包括带偏约束的 (side con straint) 和不带约束的(unconstraint)，其中经常被使用的是 2 个决策变量、2 个目标函数的 MOP。这就说明，除了搜索空间很大或目标形态 (landscape) 多样的情况，基于这些函数的 MOEA 性能比较，并不在实际应用问题方面具有很重要的意义。这种情况也许并没有反映出 MOEA 的真实的搜索能力和求解效果等。

\quad\quad 任意一个 MOP 测试集都必须包括明确的函数表达式及其特征。特别地，测试集中应当包含有对 MOEA 来说具有 “挑战性” 的函数。根据函数的结构特征，可将 MOP 测试集分为两类，不带约束的数值优化函数和带偏约束的数值优化函数 (见 附录 B 中的表 B.1 和 表 B.2，它们的 $P_{true}$ 图和 $P{F}_{true}$ 图参见 附录 C 和附录 D) 。 Van Veldhuizen 详细分析了这些函数 (Veldhuizen. 1999)，并将它们构造成一个较合理、有效的 MOEA 测试函数集，具体内容将在 3.1 小节和 3.2 小节中详细介绍。

\quad\quad 当执行一个 MOEA 的时候，潜在地假设了问题领域的知识已经恰当地被包含到算法中，因此可以得出该 MOEA 适用于搜索该问题解的结论。这时基因所代表的含义是确定的，算法的探索是有效的，搜索的操作也是明确的。研究的目的是使得算法找到的 $P{F}_{known}$ 和 $P_{known}$ 分别收敛到 $P{F}_{true}$ 和 $P_{true}$

\quad\quad 表 11.1 和表 11.2 分别列出了部分 MOP 的特征。表 11.1 是不带偏约束的测试函数，表 11.2 是带偏约束的测试函数。表中根据函数的性质和图形概括了函数的特点，其函数图形参见 附录 C和 D。

\quad\quad 表中每一行代表了一个 MOP (参见 附录 B)，每一列分别表示基因型或表现型的特征。 $P_{true}$ 的形态可能是连续的、不连续的、均匀的或规模可变的；$P{F}_{true}$ 可能是连续的、不连续的、凹的或凸的。MOP 的特征在相应的列中用 “*” 来标示。表11.1 中的测试函数对决策变量没有偏约束，在相应的列中说明了约束条件的个数；表 11.2 中的测试函数对决策变量既有约束条件，又有偏约束条件，在相应的列中分别指出了约束条件和偏约束条件的个数。表中还给岀了 $P{F}_{true}$ 的特征，其形状可能为几何型的，也可能为拓扑型的。注意，这些函数中，只有两个 (Fonseca (2) (Fonseca et al, 1995a)和 Schaffer (Rudolph, 1998)) 具有已知的解析 $P_{true}$ 解集。

\quad\quad 对于一个函数来说，它的 $P_{true}$ 的特征包括哪些呢？几乎没有 MOEA 能够描述出一个函数的多维决策变量（基因型）的 $P_{true}$ 空间。$P_{true}$ 存在于解空间中。一个 MOP 问题是由两个或多个函数组成的，那么它的解空间就相应地会受到组合限制，如决策变量的范围和偏约束等。在这样的解空间中，$P_{true}$ 可能就呈连续的或非连续的、超面上的或独立的点，在形态上呈均匀的、规模可变的等。$P_{true}$ 中的解可能是离散的或连续的，它们由一个或多个决策变量构成。

\quad\quad 函数的 $P{F}_{true}$ 的特征又包括哪些呢？ $P{F}_{true}$ 存在于目标空间中。正如前面所列出的，它的特征包括 (非) 连续的、(非) 凸的、多维的。实际上，任意一个 Pareto 面的结构在理论上都是受到维数限制的，根据目标函数个数的变化而变化。$P{F}_{true}$ 的形态丰富，可以从单向量到高维的超面 (Veldhuizen, 1999) 。

\quad\quad 如前所述，测试函数集应当包括所有可能的基因型和表现型的特征。在这种情况下，虽然不能保证算法对所有任意的情况都有效，但至少能保证更加容易修改任意一个 MOEA 为求解某一特定问题的搜索算法，并继续保持其效果和效率。

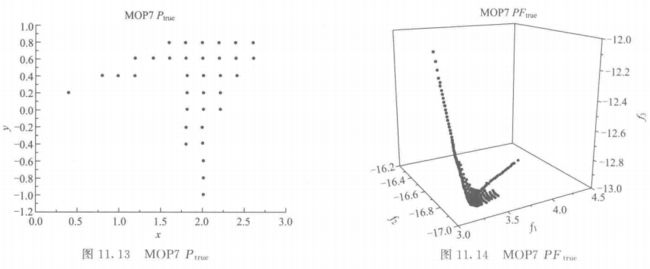
3.1 非偏约束的数值 MOEA 测试函数集

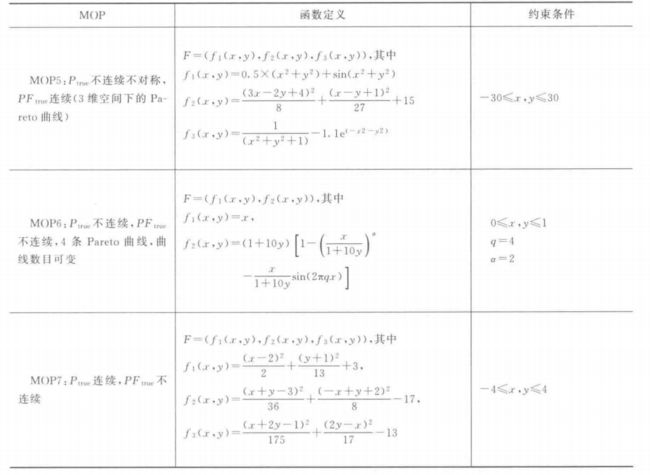
\quad\quad 前面讨论了 MOEA 的测试要求和构成 MOEA 测试函数集的条件，本节给出由 Van Veldhuizen 提出的不带偏约束的测试函数集(Veldhuizen. 1999) 。该测试函数集是通过组合现有的非偏约束测试函数而构成，符合 2. 中所讨论的测试函数的设计准则，以及表 11.1 所列出的函数的基本特征。表 11.3 给出了该测试函数集的数学表达式，图 11.1 ~ 图 11.14 分别表示每个函数的 $P_{true}$ 和 $P{F}_{true}$。为了使 $P{F}_{true}$ 更加清晰，图中的某些决策变量的范围与表 11.3 有所不同。

\quad\quad Schaffer(1) 为 2 目标函数，在该测试函数集中被命名为 MOP1。Van Veldhuizen 选择该函数的理由有三个：第一，该函数几乎被所有相关的 MOEA 使用，在测试函数中占有重要的地位，被认为是 MOP 领域中具有代表性的测试函数；第二，该测试问题具有确定的解析 $P{F}_{true}$ 表达 (Veldhuizen et al, 1999a)；第三，正如 Rudolph 指出的(Rudolph, 1998), 其 $P_{true}$ 也很容易确定。 如图 11.1 和图 11.2 所示，该函数的 $P{F}_{true}$ 是一条简单的凹的 Pareto 曲线，其 $P_{true}$ 是一条直线。Schaffer(1) 的决策变量只有 1 维，并不需要算法有很强的搜索能力，因此被认为是一个简单的测试函数。

\quad\quad 该测试函数集中的 MOP2 为 Fonseca (2)，它有 2 个目标函数，其特点是任意增加决策变量的维数即扩大其规模并不会改变目标空间中 $P{F}_{true}$ 的形状和位置(Fonseca et al, 1995a)。其 $P{F}_{true}$ 是一条简单的凸的 Pareto 曲线，$P_{true}$ 是解空间的一块连续的区域，如图 11.3 和图 11.4 所示。

\quad\quad Poloni 函数是一个 2 目标的最大化问题。如图 11. 5 和图 11. 6 所示，其 $P_{true}$ 在解空间中是两个非连续的区域，$P{F}_{true}$ 是两条非连续的 Pareto 曲线。相比其他函数，该函数从解空间到目标空间的映射相对难以理解。该函数被命名为 MOP3。

\quad\quad Kursawe 也有 2 个目标函数，其 $P_{true}$ 在解空间中有多个非连续的、非均匀的区域，其 $P{F}_{true}$ 是三条非连续的 Pareto 曲线，如图 11.7 和图 11.8 所示。同 MOP3，该函数从解空间到目标空间的映射也相对难以理解；同 MOP2，其决策变量的维数也是任意规模可变的，但是对决策变量规模的扩大和缩小会稍许改变 $P_{true}$ 的形状和位置。附录 C 中的图 C. 10 是两个决策变量的函数图形。在本节中，图 11.8 是 3 个决策变量的 $P{F}_{true}$ 图。对比两个图可以看出，$P{F}_{true}$ 和被支配的向量在目标空间中有所偏移，如果使用 4 维的决策变量，又会使得 $P{F}_{true}$ 产生其他的偏移。该函数被命名为 MOP4。

\quad\quad Viennet 函数作为第 5 类测试函数被命名为 MOP5，它有 3 个目标函数，其 $P_{true}$ 由解空间中的非连续的区域组成，如图 11. 9 所示，其 $P{F}_{true}$ 是 3 维空间中的一条 Pareto 曲线，如图 11.10 所示。

\quad\quad MOP6 是根据 Deb 的构造测试函数的方法 (见后面 4. 节) 构造的，它有 2 个目标函数。 同 MOP4，其 $P_{true}$ 和 $P{F}_{true}$ 都是非连续的，如图 11.11 和图 11.12 所示，$P{F}_{true}$ 是由 4 条非连续的 Pareto 曲线构成的。但该函数从解空间到目标空间的映射并非 MOP4 那样难以理解。 该函数用于比较 MOEA 在搜索类似的、由不同问题而产生的表现型方面的性能。

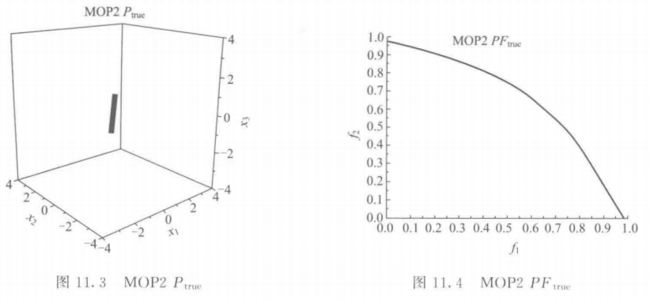
\quad\quad Viennet(2) 被命名为 MOP7，是测试函数集的最后一个函数，它有 3 个目标函数。其 $P_{true}$ 在解空间中是一片连续的区域，如图 11.13 所示，其 $P{F}_{true}$ 看起来是一个超面，并且解空间到目标空间的映射是直接的，如图 11.14 所示。该函数在测试函数集中是对 MOP5 的补充。

\quad\quad 表 11.3 中涉及的 MOEA 测试函数符合本章第 2 节中提到的设计准则。MOP1 和 MOP2 是“容易” 的多目标优化问题；MOP2 和 MOP4 是决策变量规模可变的；MOP6 是 $P{F}_{true}$ 图中 Pareto 曲线数目可变的问题；MOP5 和 MOP7 是 3 个目标函数的多目标优化问题。它们都是非线性的，在 $P_{true}$ 和 $P{F}_{true}$ 图中基本都是非对称的。将这 7 个测试函数组合形成测试函数集，就能对 MOEA 进行较全面的基本的测试和比较。当然，表 11.1 和表 11.2 中列出的具有其他特征的函数也可以放入测试函数集中，增加这些测试函数可以扩展所期望的测试函数集的特征。相对使用某个或某几个测试函数来评价 MOEA 的性能而言， 使用测试函数集的优势在于它能全面地测试 MOEA 的性能特点，从中得出的结论更加科学、可靠。

\quad\quad 在上述 Van Veldhuizen 提岀的测试函数集中，参数的改变将会突岀 $P{F}_{true}$ 的特征，并增加 MOEA 搜索的难度。如可以改变 MOP4 中的参数 $a$ 和 $b$， MOP6 中的参数 $q$ 和 $\alpha$ 等。

3.2 带偏约束的数值 MOEA 测试函数集

\quad\quad 任何综合的 MOEA 测试函数集也应该包含带偏约束的数值 MOP。求解带偏约束问题与不带偏约束问题的主要区别是，必须确保解处于可行解区域中。

\quad\quad 现有的求解偏约束问题的方法，是对个体的适应度函数值增加一个罚函数(Richardson et al, 1989)。通过罚函数的作用使得非可行解区域中的个体的适应度值远远小于可行解区域中的个体的适应度值，这样将约束问题变成不带约束的问题。另一种方法采用二进制锦标赛选择法比较两个解(HanHCetaL 2002)，处于可行解区域的解通常被选中。如果两个解都处于非可行解区域，则通过 “最靠近” 约束边界的解被选中；如果两个解都处于可行解区域，可釆用小生境等技术进行选择。可以在使用 Pareto 非支配概念和构造目标函数非支配集时分别进行约束处理(Coello Coello, 2000； Ray et al, 2001) 。通过这种方法，可以将考察的两个解分别处于解空间的什么区域分成三类：第一类是两者都是可行解 (a类)；第二类是其中一个解可行，而另一个不可行（b类）；第三类是两者都是不可行解，其中一个解相对违背约束较少（c类）。这样，当算法收敛到 Pareto 面时，可以通过分类来分别处理偏约束。当然，使算法保持分布度良好的情况下收敛到真正的 Pareto 面，与采用恰当的方法处理偏约束这两个问题是相互关联的。在初始时，MOEA 可以不用考虑偏约束，而直接在解空间内产生个体，但需要在算法的执行过程中进行 “后加工”，将非可行解区域移除掉 （这样使算法比较简单）。但要注意，“后加工”可能会删除掉过多的点。

\quad\quad 如表 11.4 所示，MOP-C1〜MOP-C5 是一个带偏约束的测试函数集。Bihn(2）函数被命名为 MOP-C1，是带偏约束的 2 目标测试函数，其 $P_{true}$ 是解空间中的一个区域，$P{F}_{true}$ 是 一条较简单的 Pareto 曲线。Osyczka(2) 函数被命名为 MOP-C2，是带强约束的 6 个决策变量的测试问题，它由 2 个目标函数组成，其 $P_{true}$ 的形状是未知的，$P{F}_{true}$ 是 3 条非连接的 Pareto 曲线。测试函数集中还选择了 Viennet（4）函数，它被命名为 MOP-C3，有 3 个目标函数，其 $P_{true}$ 是解空间中不规则的区域。第 4 个函数是 Tanaka 函数，被命名为 MOP-C4，它有 2 个目标函数和 2 个非线性的约束条件。上述 4 个函数的 $P_{true}$ 图和 $P{F}_{true}$ 图参见 附录 D。

\quad\quad 下面重点讨论不同的参数值对函数的 $P{F}_{true}$ 图的影响。正如前面所说，参数的改变将会突出 $P{F}_{true}$ 的特征，并增加 MOEA 搜索的难度。以 MOP-C4 为例，改变其参数 $a$ 和 $b$， 并且在某些情况下，对偏约束的最后一项取绝对值（记为 $abs$），其 $P{F}_{true}$ 的形状会发生如图 11.15〜图 11.20 的变化：

\quad\quad ① 标准的 Tanaka 基因型，$a=0.1,b=16$，如图 11.15 所示。

\quad\quad ② 较小的连续区域，$a=0.1,b=32$，如图 11.16 所示。

\quad\quad ③ abs，增加区域之间的距离，$a=0.1,b=16$，如图 11.17 所示。

\quad\quad ④ abs，增加区域之间的距离，$a=0.1,b=32$，如图 11.18 所示。

\quad\quad ⑤ abs，使周期变化变得更深，$a=0.1(x^2+y^2+5xy)，b=32$，如图 11.19 所示。

\quad\quad ⑥ abs，使周期变化变得更深，$a=0.1(x^2+y^2+5xy),b=8(x^2+y^2)$，如图 11.20 所示。

\quad\quad 如图 11.15〜图 11.20 所示，选择参数 $a$ 和 $b$ 的不同值会使得函数的 $P{F}_{true}$ 图发生变化，其对应的 $P_{true}$ 也会发生相应的变化。在图 11.15 中，中间的一条 Pareto 曲线由于数据的精度看起来是非连续的，但实际上是一条连续的曲线。这条曲线内部有两个区域很难找到，其原因是相关的点分别处于两个（几乎）水平和垂直的斜面上。

\quad\quad 一般来说，参数 $a$ 和 $b$ 控制着 Pareto 曲线上连续区域的长度。这些区域越小，MOEA 找到 Pareto 曲线上的点越少，越趋于离散化，区域问题变得越复杂。增加参数 $a$ 的值，区域与之间的切面长度就会增加，搜索将沿着狭窄的长廊进行，问题也会变得复杂。增加参数 $b$ 的值也会改变非连续的 $P{F}_{true}$ 区域的周期特征，使得搜索 $P{F}_{true}$ 区域变得困难。 从图中可以反映出来，参数 $b$ 的改变使可行解区域缩小。只要稍微改变参数就会使基因型空间的形态发生较大的变化。

\quad\quad 另一个较难的 MOP 由 Osyczka 和 Kundu 提出 (Osyczka et出,1995)，该函数有 6 个偏约束条件和 2 个目标函数、6 个决策变量， 被命名为 MOP-C5。该函数的 $P{F}_{true}$ 如图 11.21 所示。图中反映了满足所有偏约束条件的决策变量，在取不同值时其目标函数的分布。保持种群中的个体分布到各个区域， 对于 MOEA 来说也是个比较困难的问题。表 11.5 为该函数的 $P_{true}$ 分布，其中对于每个区域，$x_4=0,x_6=0$，其余决策变量的取值范围如表 11. 5 所示。

4. 构造 MOP 测试函数的方法

\quad\quad 构造 MOEA 测试函数最简单的方法就是利用单目标函数。Deb 详细阐述了构造多目标测试函数的系统方法及其特点（Deb, 1998, 1999）,设计一个（组）测试函数的主要依据应当是基于 MOEA 所期望的函数特征。

\quad\quad Deb 给出了两个基本定义，即 "局部” Pareto 最优解（集）和 "全局” Pareto 最优解 （集）。其中 “全局” Pareto 最优解（集）即为 $P_{true}$；通过这一术语也较容易得出 “局部” Pareto 的最优解的定义，即 $P_{local}$。 但应当注意到，$P_{local}$ 是一个易引起混淆的定义。下面看 Deb 给出的定义。

\quad\quad “局部" Pareto 最优解（集）： 给出 Pareto 最优解集 P，对 $\forall x\in P，\neg \exists y$ 满足 $||y-x|{|}_{\infty }\le ϵ$ 其中 $ϵ$ 是一个极小的正数（原则上说， $y$ 是对 $x$ 进行很小的扰动而得到的），并且 $F(x)⪯F(y)$ ($⪯$：表示偏序关系) 那么 P 中的解就构成了一个局部 Pareto 最优解集。 偏序关系介绍

\quad\quad 这个定义指出，对已给出的 Pareto 最优解集中的每个解进行较小的扰动，并不会产生新的非支配的解向量。Deb 给出这一定义的目的是指明 $P{F}_{local}$ 一般处于与其相关的 $P{F}_{true}$ “之后”。从理论上说，任意一个 $P_{local}$ 的存在都与 $ϵ$ 的取值有关，太大的 $ϵ$ 将难以产生 $P_{local}$，而太小的 $ϵ$ 将导致多重局部最优面（边界）。

\quad\quad Deb 也将这一概念扩展到多峰的、欺骗问题，仅有一个最优解、带有噪声的等多目标问题领域中。但这些扩展有两处引起争论：一是 Deb 设计了一个欺骗性的多目标问题，其中 一个至少有两个最优解（$P{F}_{local}$ 和 $P{F}_{true}$），而主要的搜索空间又偏向于 $P{F}_{local}$，这一点取决于 $P{F}_{local}$ 是否存在；第二，Deb 设计了一个多峰的多目标问题，其中一个函数有多重局部最优边界，这样的定义就会混淆概念。“多峰” 这一术语应当只能用于单目标优化函数，且包含了局部和全局极值的情况。而在多目标的情况下，组成 Pareto 面的各个向量相互之间都是互不支配的，应当不出现 “极值” 即 “峰” 的情况。因此，术语“ 多重最优面”在这里更为合适。

\quad\quad Deb 还指出，由于计算方法的不同还会导致 Pareto 面的分布性的不同。因此，他将一个非约束的多目标测试函数缩减为两个目标函数，然后再针对这两个函数给出一定的限制条件，以此来体现所期望的函数属性。可以将 Deb 的这一方法总结如下。

$$\begin{array}{l}\text{minF=(f1(x)，f2(x))}\\ \text{f1(x)=f(x1,⋅⋅⋅,xm),}\\ \text{f2(x)=g(xm+1,⋅⋅⋅,xN),h(f(x1,⋅⋅⋅,xm),g(xm+1,⋅⋅⋅,xN))}\end{array}\}$$

其中，函数 $f_1$ 是关于 $m$ 个 $(m<N)$ 决策变量的目标函数。$f_2$ 是关于所有 $N$ 个决策变量的目标函数。函数 $g$ 是关于 $N-m$ 个决策变量的函数，这 $N-m$ 个决策变量是未在函数 $f$ 中出现的，而函数 $h$ 是关于 $f$ 和 $g$ 的函数。规定 $f、g$ 必须满足 $f>0、g>0$

\quad\quad Deb 指出，函数 $f、g、h$ 在测试 MOEA 时有如下作用。

\quad\quad $f$：用于控制 Pareto 最优解集中，解向量在最优面上的均匀分布。

\quad\quad $g$：控制多目标问题解的特征，是“多重最优面”的还是单独的一个最优面。

\quad\quad $h$：控制 Pareto 面的特征，如是凸的、不连续的等。

\quad\quad 虽然函数 $g$ 和 $h$ 关于决策变量不能重叠的独立性限制了基因型的特征，但是它们使得构造包含多种特征的 “表现型” 函数容易许多。这里所指的特征包括图形成曲线或曲面、凸 的、非凸的、连续的、离散的、不相交的、规模可变的和其他特征等。研究者可以根据所需要的特征来构造岀不同的测试函数组。通过如非线性映射来构造出 $P{F}_{true}$ 的结构及所期望的不同密度的 $P{F}_{known}$。这样，MOEA 就能够通过构造好的测试函数进行比较，如收敛性 (即是否收敛到 Pareto 最优面——$P{F}_{true}$)，以及所期望的 $P{F}_{known}$ 点的分布性等。

4.1 从数值上构造 MOP

\quad\quad 以上讨论的函数将产生两方面的影响：一是沿着 Pareto 最优面的搜索，二是收敛到 Pareto 最优面的搜索；并且 Pareto 最优面的形态是 2 维的。Deb 给出的实例强调了使用这种构造方法可以构造出一个可能的 MOP 问题,例如：

在这个多目标问题中， $f_2$ 也可以写成 $\frac{g(x_2)}{x_1}$ 。因此 $g(x_2)$ 是一个具有两个极小值的函数，如图 11.23 所示。其中一个极小值为 $g(0.6)\approx 1.2$，另一个为 $g(0.2)\approx 0.7057$。 图 11.23 所示为这个多目标问题的 Pareto 最优面。其中靠上的部分为 Deb 定义的 $P{F}_{local}$，靠下的部分为 $P{F}_{true}$，属于 $P_{local}$ 部分的解集为 $(x_1，x_2)|x_2\approx 0.6$，属于 $P_{true}$ 部分的解集为 $(x_1，x_2)|x_2\approx 0.2$。

\quad\quad Deb 指出，若 MOEA 陷入局部最优即 $P{F}_{local}$， 则难以搜索到 $P{F}_{true}$。但这并不是表现型所影响的，而是基因型空间的影响。函数 $g(x_2)$ 的全局最优解在一条狭窄的峡谷中，其周围的点非常少，几乎没有。在这些很少的点中进行随机搜索，其结果是随机找到较少的 “靠近” 或处于这条峡谷中的点；而相反地，在一个较宽的区域中，局部极值的周围包含的点要多得多。因此，找到 $P{F}_{true}$ 的困难程度取决于在 $g(x_2)$ 全局极值的周围分布的点的数目，而不是简单地说 $P{F}_{local}$ 的存在导致了搜索的难度。这个例子显示了欺骗问题的特点。

\quad\quad 这个例子也强调了前文所暗示的一个问题：使连续函数（或解空间）离散化。其结果的映射可能并没有反映出问题的真实性：离散化的过程可能导致 “错误”。此外，均匀的决策变量空间的离散化并不一定产生到目标空间的均匀的映射。一般而言，在各种不同的多目标问题领域进行分析和比较 MOEA 性能时，不能轻易得出结论。不同的 MOEA 技术（包括参数和进化算子，evolutionary operators, EVOP）会产生不同的表现效果。

\quad\quad 这种构造出预期特点的多目标问题的构造方法并不是唯一的。实际的多目标问题也许有类似的基因型和（或）表现型特点，但看起来与前面所涉及的测试函数的例子都很不一样。因此，一个能够 “通过” 所有由一般方法产生的测试函数的 MOEA 并不能一定对求解实际的多目标问题有效。必须选择好测试函数（集）使之尽可能精确地反映出所描述的问题的特征。

\quad\quad 通过上述方法产生的多目标测试问题 ZDT 系列（Deb. 1998, 1999），其特征总结为表 11.6，具体的函数在表 11.7 中。其中，ZDT1〜ZDT4 及 ZDT6 的 $P{F}_{true}$ 分别如图 11.24〜 图 11. 28 所示。

\quad\quad 这一组测试函数的特点是它们都是两个目标函数的测试问题，并且其 Pareto 最优面的形态和位置等都是已知的，且是易于理解的。另一个显著的特点是这组测试函数的决策变量的个数是任意规模可变的。

ZDT1〜ZDT4 及 ZDT6

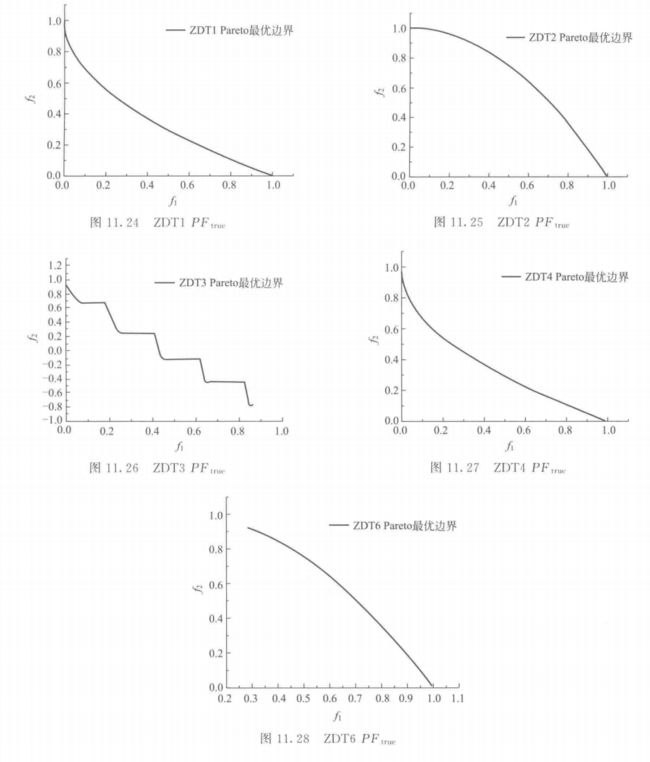
\quad\quad 用上文所述的构造方法所构造出的 MOP，其 $P_{true}$ 或 $P{F}_{true}$ 是解析的，ZDT1〜ZDT4 及 ZDT6 的 $P{F}_{true}$ 均为对应的 $g(x)=1$；ZDT5 的 $P{F}_{true}$ 为对应的 $g(x)=10$。因此，可以将 MOEA 运行结果与 MOP 最优解进行直接的比较和分析。

\quad\quad MOEA 研究者们一直都在试图构造出一组测试函数，其中包括所有普遍的 MOP 基因型/表现型的特征。对于带约束的 MOP 问题，Deb 等提出了一种使用基本公式的构造测试函数的方法(Deb et al, 2001a):

式中，有 6 个与约束有关的参数 $\theta 、a、b、c、d、e，x_1\in [0,1]$， $g(x)$ 决定了其他变量的定义域。对这 6 个参数取不同的值，就能得到不同的结构。如。$\theta =一0.2\pi ，a=0.2，b=10，c=1，d=6，e=1，P{F}_{true}$ 的图形如图 11.29 所示，图中是非连接的周期的连续区域。增加参数 $b$ 的值将增加周期的非连接区域的个数；参数 $d$ 控制了在 Pareto 最优面上连续区域的长度，当连续区域缩小时， MOEA 在 $P{F}_{true}$ 上找到的点就会很少，因为 $x$ 趋于离散化了，也就是说变成了一个更难的问题；增大参数 $a$ 的值，区域与区域之间 的 “切口 (cuts) ” 将会变得更深，使得搜 索沿着狭窄的 “走廓” 进行，也增加了问题的难度；还可以通过改变参数 $c$ 的值，使之从初始值 $1$ 开始变化，来减少一些不连接的 $P{F}_{true}$ 区域的周期，这样使得搜索所有接近 $P{F}_{true}$ 区域的点变得困难；参数 $\theta$ 和 $e$， 对 $P{F}_{true}$ 的影响不是很大，它们分别控制 $P{F}_{true}$ 的倾斜度和上下移动的变化。

\quad\quad 可以看出，这个测试函数的形式与之前讨论的 Tanaka 测试函数非常相似。离散化的基 因型变量在检测 MOEA 收敛到 $P{F}_{true}$ 的能力方面起到了非常重要的作用。虽然离散化方法被普通釆用，但独立变量之间的相互作用能够提高 $P{F}_{known}$ 向 $P{F}_{true}$ 逼近的精确度。

4.2 规模可变的多目标测试函数的构造方法

\quad\quad 上一小节讨论的 ZDT 系列测试函数都是两个目标的测试函数，虽然它们在决策变量的个数上是任意规模可变的，但是它们还不能满足对多个目标的问题进行测试的要求。因此需要构造在目标个数上也是任意规模可变的测试函数组。并且在考虑测试函数检测算法对 $P{F}_{true}$ 收敛的同时，还应当考虑检测算法在 Pareto 最优面上是否能保持良好的分布度等。此外，对实际应用问题的模拟和我们所期望的函数的特征，也是在构造测试函数时应当考虑的内容。从这些角度出发，对 MOEA 进行测试和比较，能帮助我们更加深入地理解 MOEA 的运行机理，使 MOEA 更加高效。

\quad\quad Deb 等指岀，一个能充分地对 MOEA 多方面能力进行检测的测试函数组必须包含下列特征 (Deb et al, 2001a, 2005)：

\quad\quad ① 测试函数组必须能提供可控制的 “障碍” 来影响解集对 $P{F}_{true}$ 的收敛性及其在 Pareto 最优面上的分布度。因为这两方面是多目标优化的最基本的两个目标。

\quad\quad ② 测试函数的决策变量的个数应当是任意规模可变的。这是因为许多实际应用问题常常包括大量的决策变量，为增强可行性，测试函数组中应当包括有大量决策变量的函数。

\quad\quad ③ 测试函数的目标个数也应当是任意规模可变的。虽然实际应用问题的目标数常常能减少至 4 或 5 个，但测试函数组中应当包括目标数为 15〜20 的测试函数。

\quad\quad ④ 测试函数的构造过程应当是简单的。

\quad\quad ⑤ 最终的 Pareto 最优面 (无论是连续的还是离散的) 应当是易于理解的，并且其形态和位置应当是已知的，其相应的决策变量也应当容易找到。

\quad\quad ⑥ 为了使测试函数在实际中有效，测试函数与实际应用问题的复杂性的相似程度应当是已知的。

\quad\quad 对于目标数为 2 或 3 的测试函数，其 Pareto 最优面可以在坐标轴上表示，但当目标数大于 3 时，就无法用坐标轴来清楚地描述 Pareto 最优面。因此，对于较高目标数的测试问题，如果其搜索空间具有一定的规律性，那么它的 Pareto 最优面就容易理解了。使搜索空间具有一定规律的方法是：在相关的超平面上，使 Pareto 最优面分布均匀，如 $f_1=f_2=\cdot \cdot \cdot =f_{M-1}$ (其中 $M$ 为目标个数)。这样就只需要理解函数 $f_M$ 与函数 $f_1$ 之间的相互作用，其他 的函数可以通过对称性构造出来：另一种方法是，使测试函数的 Pareto 最优面是一条曲线或者一个三维空间下的超面，这样尽管有 $M$ 个目标，但最终的解可以通过二维或三维坐标描述出来。

\quad\quad 如前所述，测试 MOEA 应当包括两个方面，一是对 $P{F}_{true}$ 的收敛性，二是在 Pareto 最优面上的分布性。因此，某些测试问题可以通过增加 “障碍” 来 “妨碍” 算法收敛到 $P{F}_{true}$，如设置函数使算法易于陷入 $P{F}_{local}$，或使其搜索偏离 $P{F}_{true}$；可以使 $P{F}_{true}$ 的形态为非凸的、离散的、在 Pareto `最优面上密度不均匀的，以此来影响算法所求解的分布性。

\quad\quad Deb 等提出了三种设计 MOEA 测试函数的方法 (Deb et al, 2005)：

\quad\quad ① 将单目标问题组合成多目标问题的方法。

\quad\quad ② 自底向上的方法。

\quad\quad ③ 对曲面进行约束的方法。

\quad\quad 第一种方法是最简单的，也是研究人员最早使用的方法。将 $M$ 个不同的单目标函数组合起来就形成了一个 $M$ 个目标的多目标测试函数，如表 11.1 中所列出的 Schaffer 函数等。 这种构造方法的主要优点在于简单易行，但是其 $P{F}_{true}$ 的结构取决于目标函数，因此其 $P{F}_{true}$ 就不是预先所知道的，可能是难以理解的。并且，即使是一个简单的多目标测试函数，如 S chaffer(2)，其 $P{F}_{true}$ 是非连续的。因此，使用这种方法构造的多目标测试函数，研究人员需要仔细的分析其 $P{F}_{true}$ 和 $P_{true}$，找到 Pareto 最优解集。

\quad\quad 另外两种构造测试函数的方法是基于已知的 Pareto 最优面的，因此在实际使用时更加的方便。具体讨论参见 4. 3 和 4.4 小节。

4.3 自底向上地构造规模可变的多目标測试函数

\quad\quad 自底向上的构造方法，首先用数学表达式精确地描述 Pareto 最优面，然后通过这个 Pareto 最优面来构造所有的目标空间，最后确定测试函数。Deb 等对该方法进行了详细描述 (Deb et al« 2005)。

\quad\quad ① 选择一个 Pareto 最优面。若有 $M$ 个目标函数，则先用 $M—1$ 个参变量来定义一个 Pareto 最优面。下面用一个例子加以说明，假设选择的 Pareto 最优面是位于三维空间中第一象限的半径为 $1$ 的八分球，如图 11.30 所示。

\quad\quad 用该八分球的参变量（$\theta ，\gamma ，r$）(这里 $r=1$) 来描述这个 Pareto 最优面为

$$\begin{array}{l}\text{f1(θ,γ)=cos(θ)cos(γ+π/4)}\\ \text{f2(θ,γ)=cos(θ)sin(γ+π/4)}\\ \text{f3(θ,γ)=sin(θ)}\end{array}\}$$

式中，$0\le \theta \le \pi /2，-\pi /4\le \gamma \le \pi /4$

\quad\quad 显然，若对三个目标都取极小值，则该八分球面上的任意两点之间的关系都是互不支配的。

\quad\quad ② 建立目标空间。利用步骤 ① 的 Pareto 最优面来建立完整的目标空间。一个简单的方法就是构造一个与 Pareto 最优面平行的面作为目标空间的一个边界，那么由这两个面作为边界所包括的区域空间就是整个目标空间。我们可以在描述 Pareto 最优面的表达式中加入一个参变量来完成这个步骤。如步骤 ① 中的示例，对式 (11.6) 增加一个关于半径 $r$ 的函数 $g(r)$)，其值大于等于 0。这样除了参变量 $\theta$ 和 $\gamma$ 之外的第三个独立的变量 $r$ 的不同取值，便可以表示目标空间中的不同的 “层”。 这样就将整个目标空间完整的描述出来了。

$$\begin{array}{l}\text{minf1(θ,γ,r)=(1+g(r))cos(θ)cos(γ+π/4)}\\ \text{minf2(θ,γ,r)=(1+g(r))cos(θ)sin(γ+π/4)}\\ \text{minf3(θ,γ,r)=(1+g(r))sin(θ)}\end{array}\}$$

式中，$0\le \theta \le \pi /2，-\pi /4\le \gamma \le \pi /4，g(r)\ge 0$

\quad\quad 上述问题的 Pareto 最优解即 $P_{true}$ 可以描述为
$$0\le \theta \le \pi /2，-\pi /4\le \gamma \le \pi /4，g(r)=0$$

如图 11.31 所示，整个目标空间为 $0\le g(r)\le 1$ 的一个区域空间。

\quad\quad ③ 构造决策变量空间。$M$ 个目标函数，需要用 $M$ 个变量来描述目标空间的任一目标向量。最后一个步骤将决策变量映射到目标向量。在这个映射过程中，可以选择任意数目的决策变量进行映射，设为 $n$。如果 $n<M$，此时并非所有的参变量都是独立的，因而会引起 Pareto 最优面维数的缩小。对于上面所涉及的三个目标的例子，三个参变量都可以认为是关于 $n$ 个决策变量的函数：

$$\theta =\theta (x_1,x_2,\cdot \cdot \cdot ,x_n)$$
$$\gamma =\gamma (x_1,x_2,\cdot \cdot \cdot ,x_n)$$
$$r=r(x_1,x_2,\cdot \cdot \cdot ,x_n)$$

\quad\quad 这些函数必须满足式 (11.7) 所定义的 $\theta 、\gamma$ 和 $g(r)$ 的范围。

\quad\quad 自底向上地构造规模可变的测试函数的方法，其过程比较简单，而且可以通过该方法产 生难易程度不同的测试函数。下面讨论这种构造方法的一些细节方面。

\quad\quad (1) 收敛到 $P{F}_{true}$ 的难度设计

\quad\quad 为增加 MOEA 从目标空间的最初搜索区域收敛到 $P{F}_{true}$ 的难度，可以简单地改变函数 $g$。 Pareto 最优面的位置和形态取决于函数 $g$ 的最小值。一个多峰的函数 $g$ 有一个全局极小值 $(g=0)$ 和若干个局部极小值 $(g=v_i)$，这样目标空间就会存在 $P{F}_{local}$ 和 $P{F}_{true}$。，测试函数变成了一个欺骗问题。

$P{F}_{true}$ 另外，即使函数 $g$ 是一个单峰函数，不同的解的密度也会导致搜索空间的不同。例如， 将式 (11.7) 中的函数 $g$ 设计为 $g=r^{10}$ 那么大量的解就会聚集在远离 Pareto 最优面的区域。如图 11.32 所示，随机产生 15000 个决策变量空间中的点，在目标空间中这些点对应的目标值较大地远离 Pareto 最优面，这种情况就会导致 MOEA 难以较快地收敛到 $P{F}_{true}$

\quad\quad (2) 穿过Pareto最优面的难度设计

\quad\quad 将目标函数的参变量和决策变量通过非线性映射对应，这样搜索空间的某些部分就会比其他部分密集许多。如在式 (11.7) 中，将参变量 $\theta$ 和 $\gamma$ 分别设计为式 (11.11) 和式 (11.12)，就会使得目标空间有不同的密集区域和密集程度。在这两种情况下，均取 $g(r)=r=x_3$。

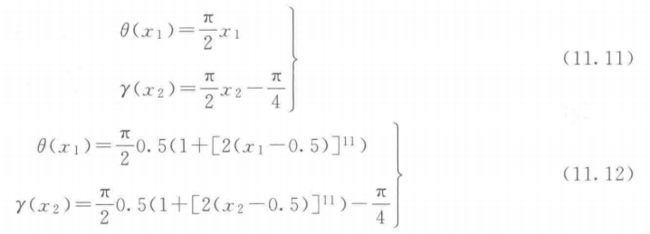
\quad\quad 为了满足式 (11.7) 的条件，取 $0\le x_1,x_2,x_3\le 1$，图 11.33 和 图 11.34 分别为在决策变量空间中随机产生 15000 个点，用式 (11.11)、式 (11.12) 及式 (11.7) 映射到目标空间的图。参变量与决策变量之间采用线性映射和非线性映射，其目标空间中点的分布有很大的不同。釆用非线性映射时，搜索的区域集中在搜索空间的中部。在这样的情况下， MOEA 要在整个 Pareto 最优面上找到具有良好分布度的解集，则具有一定的难度。

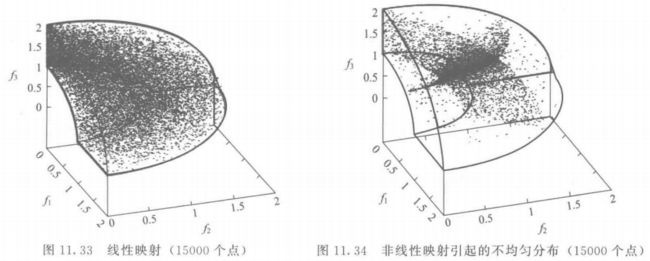
\quad\quad (3) 关于球面问题的设计

\quad\quad 下面给出基于式 (11.7)，目标数为 $M$ 的一类球面问题的测试函数：

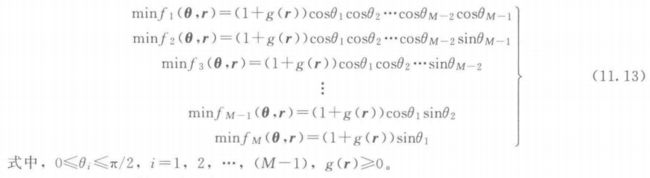
\quad\quad 注意变量的映射采用不同的方式。决策变量到参变量向量 $\theta$ (大小为 $M-1$) 的映射为
$${\theta }_i=\frac{\pi }{2}{x}_i，(i=1,2,\cdot \cdot \cdot ,(M-1))\text{\hspace{1em}(11.14)}$$

\quad\quad 在式 (11.14) 和式 (11.13) 中，对 ${\theta }_i$ 的取值约束使每一个 $x_i$ 的取值范围为 [0, 1]。剩余的 $(n-M+1)$ 个决策变量定义为 $r$ 向量 (或者 $r_i=x_{M+i-1}，(i=1,2,\cdot \cdot \cdot ,(n-M+1)))$ ，再选取一个合适的函数 $g(r)$。 显然，式 (11.13) 是一类决策变量个数大于等于目标个数 ($n\ge M$) 的球面问题的测试函数。

\quad\quad Pareto 最优面往往处于函数 $g(r)$ 取极小值的情况。例如，如果函数 $g(r)=||r|{|}^2，r_i\in [-1,1]$， 那么 Pareto 最优面为 $r_i=0$，且最优函数值必须满足下面的条件：

$$\sum _{i=1}^M(f_i{)}^2=1$$

\quad\quad 此外，测试函数 (11.13) 的难易程度可以通过不同的函数 $f_i$ 和 $g$ 来控制。

\quad\quad (4) 曲线问题

\quad\quad 既可以选择高维空间来构造 Pareto 最优面，也可以在低维空间中构造 Pareto 最优面。 在低维空间中，并不是所有的 ${\theta }_i$ 向量都是互相独立的。例如，一条在 $M$ 维空间中的曲线是一个 Pareto 最优面，那么仅仅只有一个独立的变量描述了 Pareto 最优面。使用下面的映射方法是一个简单可行的方式：
$${\theta }_i=\frac{\pi }{4(1+g(r))}(a+2g(r)x_i)(i=2,3,\cdot \cdot \cdot ，(M-1))$$

\quad\quad 式 (11.16) 的映射关系确保了在整个搜索空间中这条曲线是唯一的非支配区域。在 Pareto 最优面上，相关的 $g(r)=0$, 并且除 ${\theta }_1$ 外其余的 ${\theta }_i$ 都取为 $\pi /4$。将 曲线类问题作为测试函数，相对于球面类问题而言其优势在于：函数 $f_M$ 和任意一个函数 $f_i$ 在二维空间上的 Pareto 最优面是一条曲线 (圆或者椭圆)，除 $f_M$ 外其余任意两个目标函数 $f_i$ 在二维空间上的 Pareto 最优面是一 条直线。图 11.35 为式 (11.13) 和 式 (11.16) 在目标个数为 3 时的图形。

\quad\quad 不足之处是，靠近 Pareto 最优面的搜索区域的点，其密度相对要大得多，这样给搜索带来了方便。若要增加问题的难度，则可以采用非线性的 $g(r)$ 函数，使得当 $g(r)=0$ 时点的密集区域远离 Pareto 最优面,如 $g(r)=1/||r|{|}^a$， 其中 $a\gg 1$， 采用多峰的 $g(r)$ 函数会产生多个 $P{F}_{local}$，这样也增加了 $MOEA$ 搜索的难度。

\quad\quad 值得注意的是，该问题的不足又可以产生一个较难的最大化问题。如果对式 (11.13) 和式 (11.16) 中的每个目标都取最大化，那么处于搜索空间中顶部的面就成为 Pareto 最优面，由于只有较少的点处于这一区域，那么该问题就成为一个比较困难的最大化问题。

\quad\quad Pareto最优面从高维到低维的降低(如从面变为曲线)，在实际应用中比较常见。当多个目标并不互相冲突时，例如变速箱的设计问题有三个目标函数，即最小化变速箱的体积、 最大化功率传输和最小化输入输岀轴的距离，该问题的 Pareto 最优面实际上是三维空间下的一条曲线，而不是曲面。这是因为实际上最小化变速箱的体积和最小化输入输出轴的距离这两个目标相互之间并不是对立的。

\quad\quad (5) 测试函数的产生规则

\quad\quad 对于 $M$ 个目标函数，将问题的所有决策变量向量分为互不相交的 $M$ 个集合，即
$$x\equiv (X_1,X_2,\cdot \cdot \cdot ,X_{M-1},X_M{)}^T$$

这样便可以采用自底向上的方法构造如下的测试函数：

\quad\quad 这里的 Pareto 最优面是函数 $g(X_M)$ 取全局极小值时 (记为 $g^{\ast }$)对应的目标空间中的图形。因此 Pareto 最优面可以用式 (11.18) 来描述：
$$f_M=g^{\ast }h(f_1,f_2,\cdot \cdot \cdot ,f_{M-1})\text{\hspace{1em}(11.18)}$$

\quad\quad 由于 $g^{\ast }$ 是一个常量，于是函数 $h$（其中 $g$ 取定值 $g\ast$ ）就描述了 Pareto 最优面。在自底向上构造测试函数的方法中，研究者可以在不考虑决策变量的情况下首先选择好函数 $h$ ，即目标函数值。例如，为构造一个 Pareto 最优面为非凸的测试函数，首先选择一个非凸的函
数 $h$：
$$h(f_1,f_2,\cdot \cdot \cdot ,f_{M-1})=1-\left({\frac{{\sum }_{i=1}^{M-1}{f}_i}{\beta }}^{\alpha }\right)\text{\hspace{1em}(11.19)}$$

\quad\quad 式（11.19）中，$\alpha ＞1$。 图 11.36 为 $\alpha =2、M=3、\beta =0.5$ 的情况下，该测试问题的非凸 Pareto 最优面。

\quad\quad 将函数 $h$ 设计为多峰函数，其测试问题的 Pareto 最优面则是几段不连续的面（曲线）。

图 11.37 为在三维空间中的一个不连续的 Pareto 最优面，其中函数 $h$ 为
$$h(f_1,f_2,\cdot \cdot \cdot ,f_{M-1})=2M-\sum _{i=1}^{M-1}(2f_i+sin(3\pi f_i))\text{\hspace{1em}(11.20)}$$

\quad\quad 当函数 $h$ 已确定后，函数 $g$ 用于构造整个目标空间。值得注意的是，函数 $g$ 是定义在决策变量集合上的函数，当函数 $g$ 取最小值时，目标空间的图形为 Pareto 最优面。函数 $g$ 的其他取值就使得目标函数在目标空间中的图形为平行于 Pareto 最优面的曲面。所有位于这些曲面上的点都被位于 Pareto 最优面上的点支配。

\quad\quad 在函数 $h$ 和函数 $g$ 都已确定的情况下，$f_1$ 至 $f_M$ 为定义在决策变量互不相交的子集上的目标函数。若某个目标函数是非线性的，则在该目标下解的分布是不均匀的；若所有的目标函数都是非线性的，则在整个目标空间中解的分布都是不均匀的，这样就可以测试 MOEA 保持解的分布度的能力。另一种使目标空间分布不均匀的方法是将目标函数定义成 决策变量的相交的子集上的函数。要构造更难的测试问题，还可以将决策变量先映射到一个 中间变量向量，再在此基础上定义目标函数。

\quad\quad (6) 自底向上的构造方法的优点与不足
\quad\quad 基于自底向上的方法构造测试函数，其 Pareto 最优面是构造者明确已知的。并且构造者可以根据需要对 Pareto 最优面、问题的难易程度进行调整。决策变量的数目和目标函数的数目都是可变的。

\quad\quad 由于这种方法要求其 Pareto 最优面必须用数学表达式明确的定义出来，这样当 Pareto 最优面很复杂，难以用数学表达式明确的定义时，这种方法就不适用了。

4.4 对曲面进行约束构造规模可变的多目标测试函数

\quad\quad 与自底向上构造测试函数的方法不同，对曲面进行约束来构造测试函数的方法并不是首先就定义出一个 Pareto 最优面，而是首先确定好整个搜索空间。Deb 等对该方法进行了详细描述(Deb et al, 2005)。

\quad\quad ① 选择一个基本的目标空间。首先，确定好一个简单的 $M$ 维的有界区域，如一个超体或 $M$ 维的超面。下面用一个实例来说明确定一个超体的方法，其中每个目标函数值都确定好上界和下界：

$$\begin{array}{l}min{f}_1(X)\\ min{f}_2(X)\\ \cdot \\ \cdot \\ \cdot \\ min{f}_M(X)\end{array}\}$$
式 (11.21) 中，$f_i^{(L)}\le f_i(X)\le f_i^{(U)}(i=1,2,\cdot \cdot \cdot ,M)$。

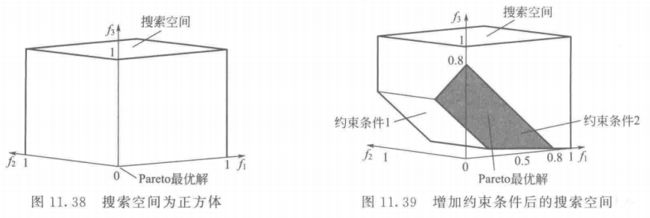
\quad\quad 直观上就知道这个问题的 Pareto 最优解集只有一个解 $(f_1^{(L)},f_2^{(L)},\cdot \cdot \cdot ,f_M^{(L)})T$，即使得每一个目标都取最小值。图 11.38 为上述问题取 $M$ 为 3 时的目标空间，以及 Pareto 最优解 $f=(0,0,0)T$。其中取 $f_i^{(L)}=0,f_i^{(U)}=1$。

\quad\quad ② 去除掉目标空间中的一部分。对目标函数加入一些约束条件 (线性的或非线性的)：
$$g_j(f_1,f_2,\cdot \cdot \cdot ,f_M)\ge 0(j=1,2,\cdot \cdot \cdot ,J)\text{\hspace{1em}(11.22)}$$

\quad\quad 这样可以去除掉最初的目标空间中的某些部分。图 11.39 为对第一步构造的正方体增加式 (11.23) 的两个线性约束条件后得到的可行区域。
$$\begin{array}{l}{g}_1\equiv f_1+f_3-0.5\ge 0\\ g_2\equiv f_1+f_2+f_3-0.8\ge 0\end{array}\}\text{\hspace{1em}(11.23)}$$

\quad\quad 剩余的空间即为可行的搜索空间。这样，就可以在可行的搜索空间中找到 Pareto 最优面，图 11.39 显示了该问题的 Pareto 最优面。为了简单化和便于理解，每个约束条件最多只对两个目标函数进行约束，如式 (11.23) 中的第一个约束条件。

\quad\quad ③ 将决策变量空间映射到目标空间中。最后一步工作是将决策向量和目标空间进行映射。将每个目标函数 $f_i$ 定义为关于 $n$ 个决策变量的线性的或非线性的函数。

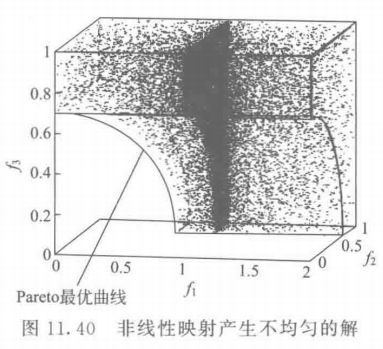
\quad\quad 如式 (11.24)，将其中一个目标函数定义为非线性的，图 11.40 为对该问题随机产生 25000 个可行解在目标空间中的图形。目标函数 $f_1$是关于 $x_1$ 的非线性函数，因此沿着 $f_1$ 的密集程度是不均匀的，在可行的搜索空间中，平面月 $f_1=1$ 并不是一个 $P{F}_{local}$， 但 $f_1=1$ 附近的点时最密集的。MOEA 在搜索时总是被 “吸引” 到这里来，主要是因为 $f_1=1$ 附近密集着许多点 (解个体)。

$$\begin{array}{l}min{f}_1(x_1)=1+(x_1-1{)}^5\\ min{f}_2(x_2)=x_2\\ min{f}_3(x_3)=x_3\end{array}\}\text{\hspace{1em}(11.24)}$$

式中，$g_1\equiv f_3^2+f_1^2-0.5\ge 0，g_2\equiv f_3^2+f_2^2-0.5，0\le x_1\le 2，0\le x_2，x_3\le 1$。

\quad\quad 函数 $f_1{f}_M$ 越复杂，搜索空间也越复杂。这样就可以构造出不同难易程度的测试函数，以检测 MOEA的搜索能力。

\quad\quad 对曲面进行约束来构造测试函数的方法，相对于自底向上构造测试函数的方法而言更加简单，可以简单地利用几何的约束来构造可行的搜索空间。因此可以构造出任意形态的（凸 的、非凸的或离散的）Pareto 最优面和目标个数规模可变的测试函数。可行的搜索空间并不是像自底向上的构造方法那样，根据 Pareto 最优面及其平行面一层一层构造出来的。所以目标空间可以根据决策变量空间的非线性映射得出。

\quad\quad 但是，用该方法产生的 Pareto 最优面一般来说难以用数学表达式精确的描述。并且， 虽然这种方法相对简单，但 Pareto 最优面的形态和连贯性并不直观易懂。另一方面，由于 Pareto 最优面可能存在于一个或多个约束的界限上，这样就要求 MOEA 采用处理约束的策略。所以说，通过这种方法构造的测试函数可以检测 MOEA 处理约束的能力。

5. DTLZ 测试函数系列

\quad\quad 根据 4.3 和 4.4 节提岀的构造测试函数的方法，Deb 等构造了一组测试函数 （Deb et al, 2005），连接作者名（family name）的首字母命名为 DTLZ 测试函数。

\quad\quad 下面对每个测试函数进行详细的描述和讨论。

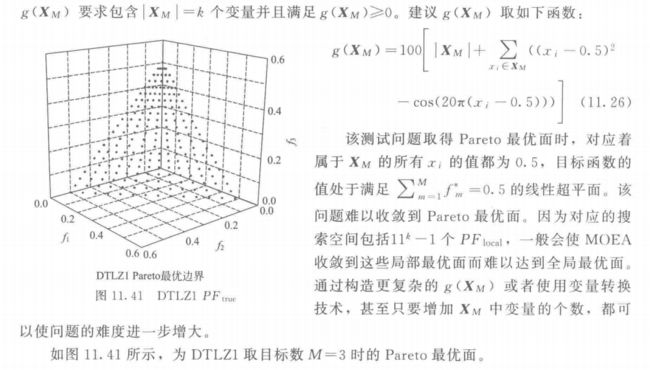
5.1 DTLZ1

DTLZ1 补充说明： $|X_M|$ 是函数 $g(X_M)$ 函数的总变量个数 $=k$，假如设定目标数 $M$ 为 3，则前面就有 $x_{M-1}$ 这个变量，共计 $M-1$ 个变量，即 2 个，如果此时设置 $|X_M|$ 为 5，则总变量数为 7，在进行种群初始化时，就需要随机初始化 7 个变量。

5.2 DTLZ2

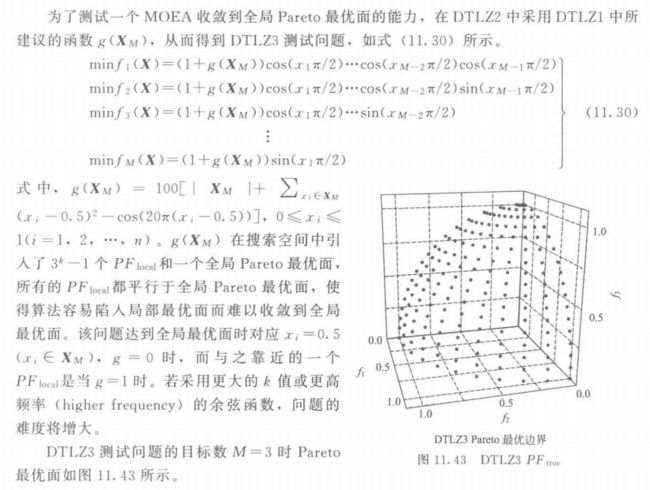
5.3 DTLZ3

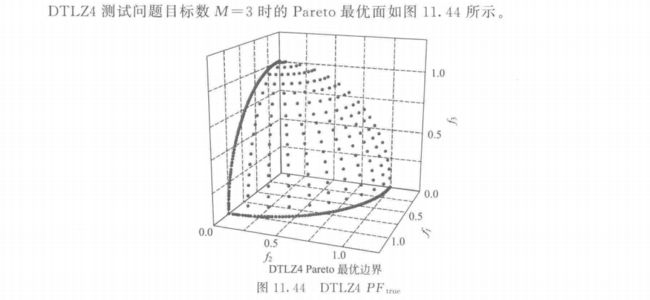
5.4 DTLZ4

5.5 DTLZ5

5.6 DTLZ6

5.7 DTLZ7

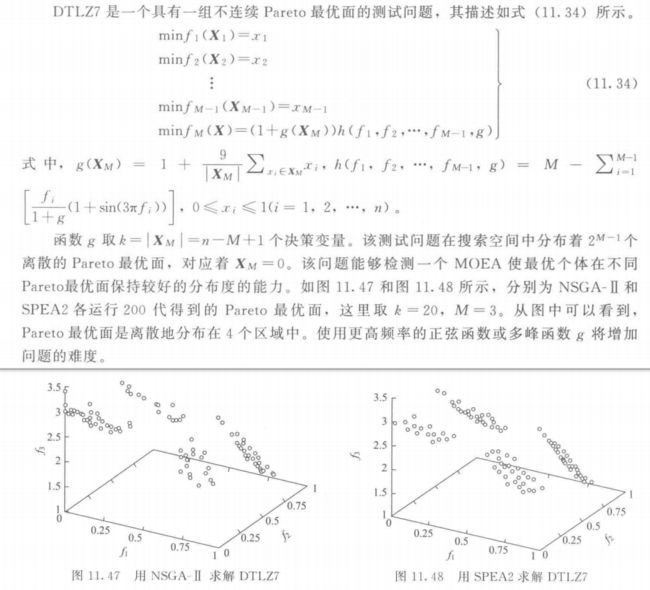
5.8 DTLZ8

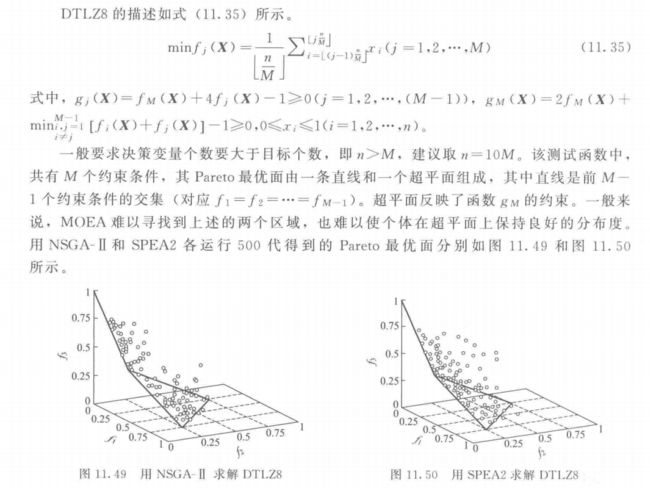
5.9 DTLZ8

6. 组合优化类 MOEA 测试函数

\quad\quad 尽管多数 MOEA 的测试函数是数值优化的，组合优化问题也常用于检测 MOEA 的性能。Garey 和 Johnson 于 1979 年提出了关于组合优化问题的定义(Garey et al, 1979) 。

\quad\quad 一个组合优化问题 $\pi$ 要么是一个最小化问题，要么是一个最大化问题。由 3 部分组成：

\quad\quad ① 一个实例问题领域 $D_{\pi }$

\quad\quad ② 对每一个实例 $I\in D_{\pi }$， 都有一个确定的候选解集 $S_{\pi }(I)$

\quad\quad ③一个函数 $m_{\pi }$， 它将每一个实例 $I\in D_{\pi }$ 的每一个候选解 $\sigma \in S_{\pi }(I)$ 都映射为一个正的有理数 $m_{\pi }(I,\sigma )，$ 函数 $m_{\pi }(I,\sigma )$ 被称为解 $\sigma$ 的值。

\quad\quad 当一个 MOEA 搜索这个有限的 (离散) 解空间时，必须有特殊的进化算子来确保只有可行解(即 $S_{\pi }(I))$ 才能被考虑 (也就是说，需要一个修正函数)。但是，组合优化问题的基因型与数值优化函数的基因型是大不相同的。组合优化类 MOP 可能在目标空间中的点是离散的，有时还仅只是单独的几个点。因此，对只有有限个解的情况，即使这些解向量可能在画图时能连成一条连续的曲线 (面)，但对于它们所组成的 $P{F}_{true}$ 来说，有些点的位置根本就没有对应的解存在，或者说其对应的解是不可行的。

\quad\quad 组合优化类 MOP 在实际生活中有很多，如以 $0-1$ 背包问题为例。

\quad\quad 对于含 $n$ 个背包、$m$ 个物品的多目标 $0-1$ 背包问题，其目标函数为
$$maxf(x)=(f_1(x),\cdot \cdot \cdot ,f_n(x))\text{\hspace{1em}(11.37)}$$

其中，$f_i(x)={\sum }_{j=1}^m{p}_{i,j}{x}_j$。$p_{i,j}$ 是当 $x_j$ 为 $1$ 时，将物品 $j$ 放入背包 $i$ 的价值。约束条件为式(11.38)，其中 $w_{i,j}$ 是物品 $j$ 放入背包 $i$ 的重量，$c_i$ 是背包 $j$ 的容量。
$$\sum _{j=1}^m{w}_{i,j}{x}_j\le c_i\text{\hspace{1em}(11.38)}$$

\quad\quad 多目标最小生成树问题 (multiobjective minimum spanning tree, mo-MST)，也是一类比较典型的 MOP。图中的每一条边有 $k$ 个权值，用 $k$ 个非负实数来表示，即 $k$ 为元组。该类问题的目标是要找到所有 Pareto 最优的最小生成树，即解集中按边权顺序构成的生成树都是互不支配的。这类问题可以通过改变某些参数而成为能比较 MOEA 性能的测试标准。 如可以通过 “选择不同方法生成边的权值来产生非欧几里得距离的 mo-MST 问题：随机不相关的、相关的、反相关的或 $m$ 度向量相关的。从部分图或完全图可以得到凹的或其他几何形态的最优 Pareto 面。如果问题是带最大的顶点度的约束问题，那么可以定义成多目标度约束的最小生成树问题。

\quad\quad 另外，如旅行商问题、着色问题、顶点覆盖问题、最大独立集问题、作业调度问题、车 辆路由问题、规划问题等，都可以用作 MOEA 的测试问题。

\quad\quad 实际上，这些问题都是对解向量 $x$ 带有约束的优化问题，它们多为 $NP$ 完全问题，因此其解可能是离散的值（如整数）。将这些问题作为 MOEA 的测试问题需要斟酌：一方面， 用 EA 解决这类优化问题时，通常都用到特殊的有针对性的基因表示和进化算子，这就很难进行一般的 MOEA 性能的比较；另一方面，NP 完全问题本身的难度也可以作为对算法的 “挑战”，同时也是对其他 MOP 测试问题的补充。

\quad\quad 值得说明的是，不同的 NP 完全问题可以变换成背包问题或旅行商问题，前者目标空间的 Pareto 最优面是较光滑的，而后者的 Pareto 最优面是一些小的面，因此后者更难以找到 Pareto 最优面。

7. WFG 测试问题工具包

\quad\quad 2006年，Huband 等对当时几种流行的测试问题集进行了总结性分析，并提出了一 个可扩展的 WFG 测试问题工具包（Huband et al, 2006)。该工具包不仅提供了多种问题特性（如欺骗、偏转、多模等）函数，以及一组包含多种几何结构的形状函数，我们可以利用这些工具函数通过一种自底向上的方式构造具备多种特性、难度可控的测试问题。

7.1 问题特性

\quad\quad 从测试问题的设计角度来看，决策空间到目标空间（决策一目标）映射关系是非常重要 的，特别是 PS 和 PF 之间的映射关系（其中， PS 和 PF 分别为决策空间和目标空间中的 Pareto 最优解集），前者决定了搜索的难度，而后者则决定了什么样的解是一个 Pareto 最优解，直接影响着算法能否搜索到整个 Pareto 最优解集。然而，一些问题特性往往通过改变 映射关系来影响算法的搜索过程。

\quad\quad 由于测试问题集的种类和数目非常之大，出于实际情况考虑，在本小节所涉及的定义、 概念以及方法均是针对一类特定的测试问题：多目标的，不带边界约束的，决策变量是实值 的并且目标为定义良好的数学函数。

\quad\quad 映射关系可以是一对一或者多对一的。对于优化算法来说，多对一具有更高的难度，因为算法必须对两个在目标空间相等的个体（决策向量）做出评价，并保留相对较好的个体 （决策向量）。同样地，PS 和 PF 之间的映射关系也可能是一对一或者多对一的，在这种情况下，我们称该问题是 Pareto 一对一或者 Pareto 多对一的。

\quad\quad 多对一映射的一个特殊例子是在一个连续的决策空间内的所有决策向量对应目标空间中的单一值，则称这一特征为平坦区域。在这一区域中，决策空间中变量发生一定的扰动并不会改变其目标值，而优化算法对这一区域上的参数变量往往因为缺少有效的梯度信息而难以优化。假如某一问题的映射关系中绝大部分都是平坦区域，并且没有 Pareto 最优解的位置信息，则称其最优解为孤立解（isolated optima）,带有孤立解的问题往往具有很高的难度。

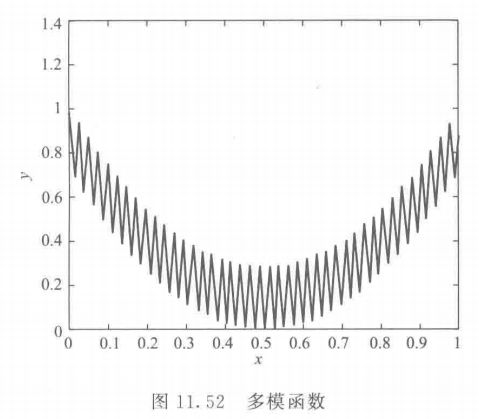
\quad\quad 多模特性也是映射关系中的一个重要特性。如果一个目标函数具有多个局部最优，则称其是多模的；相对应地，如果一个目标函数只有一个最优值，则称为单模的。具有多模目标函数的问题称为多模问题。如图 11.52 所示，该多模函数具有 20 个极小值，当 $x=0.5$ 时取得全局最优，其他极值点均为局部最优。

\quad\quad 多模目标函数的一个特殊情况是带欺骗的目标函数。根据 Deb 的相关论述（Deb, 1999），如果一个目标函数是欺骗性的，那么它至少包括两个最优值，一个为真正的最优， 一个为欺骗性最优，并且搜索空间的绝大部分区域必须位于欺骗性最优区域的范围内。真正的最优所对应的搜索区域则非常狭窄，使其被算法搜索到的概率非常小，从而容易陷入局部最优。对于优化算法来说，多模问题具有较高难度的原因，正是因为其极易陷入局部最优。 如图 11.53 所示，该欺骗函数的全局最优为 0，并且包含两个局部最优 0，1，其全局最优对应的搜索区间宽度为 0.001 。

\quad\quad 映射关系中的另外一个重要特性是偏转，这一特性使得一组分布均匀的决策向量映射到目标空间后将不再是均匀的。偏转特性对整个搜索过程会产生重要影响，特别是当 PS 与 PF 的映射关系中存在偏转的情况下。判断一个问题是否存在偏转的方法是，给定一组均匀分布的解，观察其在目标空间中的分布密度（目前还没有文献使用数学方法对偏转进行明确 的定义）。本节中，只有当一个问题被刻意地结合了偏转特性时，才称之为偏转问题。

\quad\quad 参数依赖也是测试问题应该具备的特性之一。给定单一目标 $O$、决策向量 $X$，则定义 一个变量 $x_i$ 上的子问题 $P_{O,X,i}$，该子问题的全局最优为 $P_{O,X,i}^{\ast }$， 如果 $P_{O,X,i}^{\ast }$ 只与 $x_i$ 相关, 而与决策向量 $X$ 中其他参数无关，则称 $x_i$ 是可分离的。也就是说，当改变 $x_i$ 的值使目标 $O$ 达到最优 $P_{O,X,i}^{\ast }$ 时，此时保持 $x_i$ 不变，而改变其他参数的值将不会对目标 $O$ 的值产生影响。可分离性这一概念，是针对某一个变量（$x_i$）相对于决策向量而言的，而对于特定目标 $O$，如果 $x_i$ 是可分离变量，那么目标 $O$ 必然与 $x_i$ 是相关的。如果某一个目标 $O$ 的所有变量都是可分离的，则可以逐个优化决策向量X中的变量，使问题R槌达到最优。同样 地.如果一个问题中的所有目标都是可分离目标，则称该问题为可分离问题。在多目标优化 中，如果一个问题是可分离的，那就意味着每个目标上的理想点（或最优点）都可以通过优 化某一个参数小来获得，由此可知，优化一个可分离的多目标问题要比优化一个同等规模 的不可分离问题容易得多。

\quad\quad 根据决策变量本身在映射关系中发挥的作用，可以将决策变量分为位置参数和距离参数两种类型。位置变量决定了一个多目标优化问题中解的分布情况。而距离变量则决定了解的收敛情况。一个变量 $x_i$ 为位置参数，当且仅当，改变一个解 $a$ 中的参数 $x_i$ 所产生的新的解 $a^{{}^{\prime }}$ 与 $a$ 互不支配，或与 $a$ 相同。一个 $x_i$ 为距离参数，当且仅当，改变一个解 $a$ 中的参数 $x_i$ 所产生的新的解 $a^{{}^{\prime }}$ 或者支配 $a$，或者被 $a$ 支配，或与 $a$ 相同。也就是说，通过改变位置参数可能产生多样性更好的解，而通过改变距离参数可能产生收敛性更好的解。在一些特殊情况下，位置参数或者距离参数到目标函数之间可能存在多对一映射关系，这时改变一个解 $a$ 中的位置参数或者距离参数所产生的新解 $a^{{}^{\prime }}$ 可能与 $a$ 相同。

\quad\quad 表 11.8 中，列举出了本小节中所涉及的主要特性的函数形式，包含了偏转、变换和降 维三种类型。

7.2 Pareto 最优面的几何结构

\quad\quad 单目标问题中，最优解是一个点；而多目标问题中，其 Pareto 最优面可能为线型、凸 型或凹型，也可能由多个不同类型几何形状的结构组成。线型或者 (超) 平面型是这些类型的一种特殊情况。

\quad\quad 一个退化型结构是指 Pareto 最优面的维数必须少于其目标维数。例如，若一个 3 维目标问题的 Pareto 最优面是一个线段，那么该问题是退化型的。然而，若一个 3 维目标问题的 Pareto 最优面是一个 2 维流形，那么该问题则不是退化问题。对于一些算法而言，在优化一个退化型 Pareto最优面时会产生一些难以预料的问题。如果算法试图使用一些依赖于目标维数的分布性保持策略，那么对于退化型问 题，则应该尽量避免釆用这种策略。

\quad\quad Pareto 最优面也可能是非连通的 (非连续或者间断)，也许这更加符合某些实际情况。如图 11.54 所示，由于位于分段区域上的个体被点 A 所支配，导致该 Pareto 最优面变为非连通型。

\quad\quad 表 11.9 中列举岀了本小节中所讨论的几何结构的函数形式，包括线型、凸型、凹 形、混合型以及退化型。

\quad\quad 读者可以结合经典的测试问题集来加深对这些问题特性的认识和理解。例如，在 ZDT 系列测试问题 (Zitzler et al, 2000) 中，ZDT6 的 $f_1$ 结合了复杂的多模函数，而 ZDT3 则具备了非连续型的几何结构；在 DTLZ 系列问题(Deb et al, 2005)中，DTLZ4 中的所有位置参数都结合了偏转，而 DTLZ5 则是典型的退化型问题。

7.3 构造测试问题的一般方法

\quad\quad 为了提高测试问题的质量，在使用该工具包构造问题时，应做到以下几点。

\quad\quad ① 决策向量中应避免出现极值变量。考虑距离参数的最优值位于区间的边界的情况， 如果算法通过截断操作来处理越界个体，并用区间边界值代替该参数的值，那么对于极值参数来说.这一操作将 “意外地” 达到了最优。相反地，使用区间边界值对称方法来处理越界个体的算法将很难优化极值参数。

\quad\quad ② 决策变量中应避免出现中值变量。如果通过初始化过程产生的个体对称地、均匀地分布于最优解两侧，使用带高斯（均值为0）扰动的中值重组方式产生后代个体，进行独立重复试验，则所产生的子代种群是最优解的无偏估计。也就是说，一个随机初始化的种群， 采用中值重组方式将有利于搜索中值变量。

\quad\quad ③ 决策向量维数和目标向量维数应是可扩展的；决策向量中各个维度的变量值域应是不同的，同样地，Pareto 最优面在各个维度上的值域也应是不同的。

\quad\quad ④ Pareto 最优解集应是已知的。很多评价指标要求 Pareto 最优面是已知的，这有利于更加准确地对不同算法进行评价。

\quad\quad ⑤一个测试集所包含的测试问题应该包含尽可能多的特性，然而在多目标领域设计一 个这样的测试问题集却是十分困难的。正如在前两个小节中所提到的，测试问题应该具备多样的几何结构，具备参数依赖、偏转、多对一映射、多模等特性。具体如下：

• 设计具有不同几何结构或者偏转状态的单模问题，以测试算法的收敛能力。
• 测试问题应包含以下三种重要的几何结构：PF 退化型，PF 非连续型，PS 非连续型。
• 测试集中大部分问题应该是多模的，并且具有少数欺骗问题。
• 测试集中大部分问题应该是不可分离问题，并且具有不可分离的多模问题。
• 如有需要，测试集中应具备多对一问题，以测试算法保持多样性的能力。

\quad\quad 需要特别说明的是，这些问题特性（函数）可以根据不同的设计需求引入到不同的位置中。例如，对于多模，由于搜索到多模函数的全局最优相对难度较大，因此如果对位置参数引入多模将直接对解在目标空间的分布广泛性（甚至是分布均匀性）产生影响，如果对距离参数引入多模则直接影响到解的收敛过程。同样的，对于欺骗，由于欺骗函数的全局最优位于一个相对狭小的区间内，搜索到该函数的全局最优比较困难，如果对位置参数引入欺骗特性将直接 影响解在目标空间的分布广泛性（一般不会对分布均匀性产生影响），如果对距离参数引入欺骗也将直接影响到解的收敛性。尽管引入欺骗和多模所产生的影响是相似的，但是两种特性所 注重测试的性能是不同的，多模函数注重的是算法的全局搜索能力，而欺骗函数则更加倾向于 局部搜索能力。对不同参数引入偏转或者带平坦区域的情况，在此不再赘述。

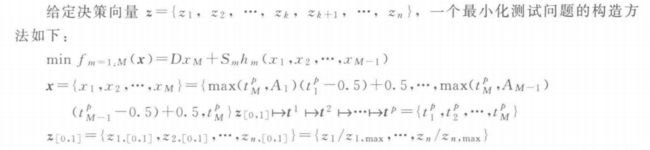
\quad\quad 在上述构造过程中，$x$ 为中间参数向量，$x_{1:M-1}$ 为对应向量的位置参数；$z$ 为实际参数向量，$z_{1:k}$ 为位置参数，$z_{k+1:n}$ 为距离参数；$z_{[0,1]}$ 由 $z$ 各维参数标准化产生。由 $z_{[0,1]}$ 产生 $x$ 过程中包含 $p$ 次转换过程和一次退化处理过程，每次转换过程使用一个转换函数，即表 11.8 中某个特定的特性函数；对于 $t^p$ 中的每一维参数 $t_i^p，max(t_M^p,A_i)(t_i^p-0.5)+0.5$ 为退化处理过程，$A_{1:M-1}\in \{0,1\}$ 为响应系数，如果 $A_i$ 为 0，那么测试问题的 Pareto 最优面的维数减 1。$h_{1:M}$ 为特定结构的形状函数，$D$ 和 $S_{1:M}$ 分别为距离参数和形状函数的扩展参数。关于转换过程 $\mapsto$ 的更多讨论，读者可参阅相关文献（Huband et al, 2006）。通过上述标准化的构造过程，可以构造出一个 WFG 测试问题实例，并且具备了多种用户定义 的问题特性和特定的几何结构。

7.4 WFG1-WFG9

\quad\quad 表 11.10 中列举出了 9 个 WFG 问题，表中详细说明了各个测试问题构造过程中所使用的特性函数、形状函数以及其他重要特性。

8. 可视化测试问题

\quad\quad 在多目标进化优化中，高维问题（目标数大于3）的解集可视化是一个具有挑战性的研究课题（Li Met al, 2014）。一般地，在目标空间中解集的可视化方法可以归为两类：第一 类,在平面上直接表示目标向量，常用的如平行坐标系图（Debet al, 2001a; Inselberg et al, 1990, 2014）。该类方法不足之处是无法获得目标向量之间的 Pareto 支配信息。第二类， 将高维目标向量映射为 2 维或 3 维可视化的目标向量。这类方法需要考虑目标向量之间的 Pareto 支配关系以及它们在种群中的位置信息，十分复杂。近年来，从另外一个角度研究可视化方法获得了较好进展，即在低维决策空间中，通过观察决策向量的分布来分析目标解集的收敛性和分布性。

\quad\quad Li Miqing 等从决策空间的角度考虑，构造了 Rectangle 可视化测试问题（Li M et al, 2014）,下面予以论述。

\quad\quad Rectangle 问题的关键特性是 Pareto 最优解集在决策空间中的图像与它们在目标空间中的图像是相似的（从欧几里得几何距离角度分析）。实际上，任何两个决策空间 Pareto 最优解之间的距离与它们对应的目标空间中目标向量之间的距离的比值是一个常量。因此，可以通过观察低维决策空间中 Pareto 最优解集的收敛性和分布性，来分析对应目标向量集的表 现性能。

\quad\quad Rectangle 问题的 Pareto 最优解集在决策空间中全部位于一个矩形区域内。该测试问题主要考虑决策向量到平行于坐标轴的一些平行线之间的距离。 图 11.55 是 Rectangle 测试问题的一个例子，收敛时， Pareto 最优解将全部位于由 4 条平行线 A、B、C、D 包围的阴影区域（包括边界线）内。

\quad\quad 4 维 Rectangle 问题的优化目标是最小化某个个体 $x=(x_1,x_2)$ 到 4 条平行于坐标轴的直线之间的欧几里得距离，其中 $a_1$ 和 $a_2$ 是平行于第一条坐标轴的 2 条直线，$b_1$ 和 $b_2$ 是平行于第二条坐标轴的 2 条直线。 4 维 Rectangle 问题的表达式为

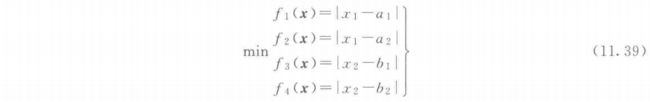
\quad\quad Rectangle 测试问题中决策空间 Pareto 最优解集的图像与它们在目标空间中的图像的几何相似性可以证明。给定表达式（11.39）中的两个 Pareto 最优解 $x^1=(x_1^1,x_2^1)，x^2=(x_1^2,x_2^2)$（不失一般性，假设 $a_1<a_2$ 和 $b_1<b_2$），则决策空间中这两个最优解之间的欧几里得距离为
$$D(x^1,x^2)=[((x_1^1-x_1^2{)}^2+(x_2^1-x_2^2{)}^2{]}^{0.5}\text{\hspace{1em}(11.40)}$$

则这两个个体在目标空间中的欧几里得距离可以推导得：

$$D(f(x^1),f(x^2))=\sqrt{2}D(x^1,x^2)\text{\hspace{1em}(11.41)}$$

\quad\quad 由式（11.41）可以得岀 2 个个体在目标空间中的欧几里得距离与其在决策空间中的距离的比值为一个常数，因此可以证明 Rectangle 测试问题中决策空间 Pareto 最优解集的图像与它们在目标空间中的图像在几何上是相似的。

\quad\quad 将 2 维决策变量扩展到 3 维时，目标维数由 4 维相应地扩展到 6 维，则 6 维 Rectangle 问题的优化目标是最小化某个个体 $x=(x_1,x_2,x_3)$ 到 6 条平行于坐标轴的直线之间的欧几里得距离。Pareto 最优区域是由这 6 条平行线围成的长方体。

\quad\quad Rectangle 问题的目标维数（平行于坐标轴的直线）是由决策向量的维数决定的（仅有两条直线平行于同一条坐标轴），而在保持决策向量维数不变的情况下，添加新的平行直线是较困难的（当有多于两条直线平行于一条坐标轴时， 违背了 Pareto 最优解集在决策空间中和在目标空 间中的图像之间的几何相似性）。因此，Rectangle 问题未能扩展到任意的目标维数。
\quad\quad Rectangle 问题不仅能使 Pareto 最优解集的收敛效果和分布效果可视化，也能如同 DTLZ 系列测试函数一样，被用来测试 MOEA 收敛到 Pareto 最优区域的能力。如图 11.56 所示，为 SPEA2 + SDE （该算法可参见 7.4 节）收敛到 4 维 Rectangle 问题时的 Pareto 最优区域。

9. 其他测试问题