AES与RSA的填充模式
目录
AES(分组密码)的填充 [1]
1. PKCS5 Padding
2.OneAndZeroes Padding
3. ANSI X9.23 Padding
4. W3C Padding
RSA的填充
RSA_NO_PADDING
RSA_PKCS1_PADDING
RSA_PKCS1_OAEP_PADDING[3]
RSA_PSS[4]
RSA和AES虽然属于两种截然不同的加密类型,但它们都属于块密码的应用范畴。AES的块大小是固定的16字节,RSA的块大小根据密钥长度和填充方式而定。由于AES每次只能处理固定长度的数据(即一个块大小),当数据大小不是块大小的整数倍时,就需要对原始数据进行填充,因此填充对AES来说是技术原理上的需求。RSA则不太一样,RSA填充的主要目的是为了加强算法的安全性。RSA填充在安全上的作用体现在以下两个方面:一方面,填充后明文长度变长,对应的密文长度也变长了;另一方面,某些填充方式会在明文中加入伪随机信息,将给定的明文消息加密为不同的密文。
AES(分组密码)的填充 [1]
使用ECB或CBC模式进行块密码加密时,输入的密文长度必须是块大小B(以字节为单位)的整数倍。对于3DES,块大小B是8字节(64 位);对于所有 AES 变体,块大小是 16 字节(128 位)。如果要加密的数据长度不是B的整数倍,则必须将其长度填充为B的整数倍。解密后,需要去除填充的数据。
对于其他加密模式,例如“计数器”模式 (CTR) 或OFB或CFB,则不需要填充。在这些情况下,密文总是与明文长度相同,填充方法不适用。(不需要填充的原因见如何选择加密模式一文)
填充规则的类型有很多种,最流行的是“PKCS5”。PKCS5填充在[PKCS5]的6.1.1节中定义,与[CMS]的6.3节、[PKCS7]的10.3节和[RFC1423]的1.1节中的填充方法相同。
1. PKCS5 Padding
如果块大小为B,则添加N个值为N的填充字节以使输入长度达到B的下一个整数倍。如果输入长度已经是B的整数倍,则添加B个值为B的字节。解密后,检查解密数据的最后N个字节是否都具有N值且1 < N ≤ B。如果是,则去掉N个字节,否则抛出解密异常。
块大小B = 8的PKCS5填充示例:
3 bytes: AEAEAE --> AEAEAE0505050505
7 bytes: AEAEAEAEAEAEAE --> AEAEAEAEAEAEAE01
8 bytes: AEAEAEAEAEAEAEAE --> AEAEAEAEAEAEAEAE08080808080808082.OneAndZeroes Padding
对于“OneAndZeroes”填充,添加一个值为 0x80 的字节,后跟尽可能多的零字节,以将输入填充到B的下一个整数倍。与 PKCS5 填充一样,此方法总是将长度介于 1 和 B 字节之间的填充添加到加密前输入。解密后很容易以明确的方式将其删除。
“OneAndZeroes”的名称来源于其实施填充的方法,该方法在输入后附加一个值为“1”的比特位,然后根据需要添加值为“零”的比特位,直到长度达到B的整数倍。填充的第一个字节的二进制值为10000000,转换为16进制表示即为0x80。
块大小B = 8的 OneAndZeroes 填充示例:
3 bytes: AEAEAE --> AEAEAE8000000000
7 bytes: AEAEAEAEAEAEAE --> AEAEAEAEAEAEAE80
8 bytes: AEAEAEAEAEAEAEAE --> AEAEAEAEAEAEAEAE80000000000000003. ANSI X9.23 Padding
如果需要N个填充字节(1 < N ≤ B),则将最后一个字节的值设为N,并将前面N-1个填充字节的值设为零。
块大小B = 8的 AnsiX923 填充示例:
3 bytes: AEAEAE --> AEAEAE0000000005
7 bytes: AEAEAEAEAEAEAE --> AEAEAEAEAEAEAE01
8 bytes: AEAEAEAEAEAEAEAE --> AEAEAEAEAEAEAEAE00000000000000084. W3C Padding
W3C Padding的描述在XMLENC(W3C推荐的加密标准)的第5.2.1节。在W3C Padding填充规则中,如果需要N个填充字节 (1 < N ≤ B),则将最后一个字节的值设为N,将前面N-1个填充字节的值设为任意值。
列举此方法是为了内容的完整性,实际上我们并不推荐使用W3C Padding,因为只依据一个字节推断所有填充字节的逻辑存在漏洞。在实际的应用中,我们推荐使用 PKCS5填充,这种填充的逻辑更加严格。
块大小B = 8的W3C填充示例,其中“xy”是任意字节:
3 bytes: AEAEAE --> AEAEAExyxyxyxy05
7 bytes: AEAEAEAEAEAEAE --> AEAEAEAEAEAEAE01
8 bytes: AEAEAEAEAEAEAEAE --> AEAEAEAEAEAEAEAExyxyxyxyxyxyxy08RSA的填充
RSA_NO_PADDING
如果选择RSA_NO_PADDING模式,在明文不够128字节(假设密钥长度128 bytes/1024 bit,后文基于同样的假设)的情况下,加密时会在明文前面填充若干0字节,直至长度达到128字节。 解密后的明文也会包括前面填充的零,用户需要注意把解密后的字段前向填充的零去掉,才是真正的明文。
RSA_PKCS1_PADDING
RSA_PKCS1_PADDING即PKCS#1 v1.5,属于PKCS#1的一个早期版本。在该填充模式下,如果明文长度不够128字节,加密的时候会在明文中随机填充一些数据,结果是相同的明文每次加密后的密文都不一样。 PKCS#1 v1.5的具体填充规则如下:
EB = 00 || BT || PS || 00 || M ,其中M为消息
BT代表块类型:
1. 当BT=00 or 01 时,表示当前进行私钥运算;
2. 当BT=02 时,表示当前进行公钥运算;
PS代表填充字符串:
1. 当BT=00,PS由00组成;
2. 当BT=01,PS由FF组成;
3. 当BT=02,PS由伪随机生成,且非零。
PS长度为len(EB) - 3 - len(M),最少8个字节。PKCS#1 v1.5填充方式存在安全隐患,该安全隐患的根本原因来自EB的头两个字节是固定的,导致该模式在某些场景下(如客户端在于SSL/TLS 服务器握手的过程中,服务器会对头两个字节的正确性给出反馈)抵抗不住选择密文攻击。详细的攻击过程可以阅读Daniel Bleichenbacher的论文《Chosen Ciphertext Attacks Against Protocols Based on the RSA Encryption Standard PKCS #1》[2]。
RSA_PKCS1_OAEP_PADDING[3]
为了弥补PKCS#1 v1.5版本的安全缺陷,PKCS提出了全新的填充模式——OAEP(Optimal Asymmetric Encryption Padding),也就是PKCS#1 v2。OAEP通过引入两个MFG函数来实现填充后文本的随机性,填充流程如下所示:
OAEP填充流程(图片来自维基百科)
其中,m表示原始明文,长度为n-k0-k1,n为密钥长度;G、H为两个MGF函数,G将长度为k0的输入转换成长度为n-k0的输出,H则恰好相反;⊕为异或运算;最终的填充数据为X||Y。填充流程描述如下:
1. 使用k1个0字节将长度为n-k0-k1的明文m填充至n-k0;
2. 长度为k0的随机数r经过G运算后与步骤1的结果异或,得到长度为n-k0的X;
3. X经过H运算后与r进行异或,得到长度为k0的Y;
4. 拼接X和Y得到加密运算的输入数据EB。
经过OAEP的填充之后,EB不再具有固定值的字节,其安全性相比于PKCS#1 v1.5得到了很好的加强。
RSA_PSS[4]
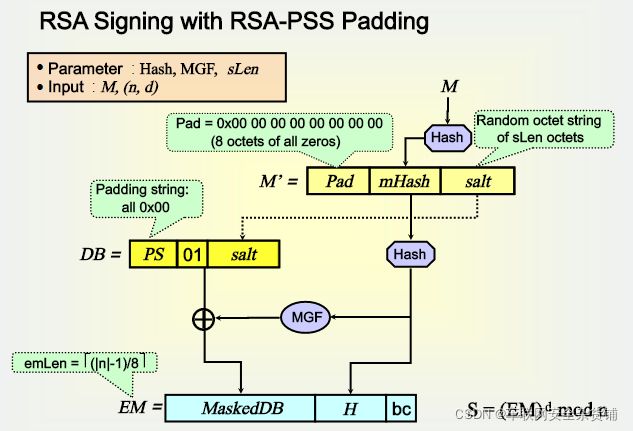
RSA_PSS(Probabilistic Signature Scheme)是由 Mihir Bellare 和 Phillip Rogaway 设计的私钥签名过程中使用的一种填充方式,是 PKCS#1 v2.1 标准的一部分,用来取代RSA-PKCS #1 v1.5。PSS填充过程如下图所示[5]:
对比PKCS#1 v1.5的填充模式:
0x00 0x01 [ 0xff bytes ] 0x00 [ hash type & hash ]PSS的填充模式更加复杂和不可预测,在安全性上也远高出PKCS#1 v1.5。
参考文章
[1]. Padding schemes for block ciphers
[2]. http://archiv.infsec.ethz.ch/education/fs08/secsem/bleichenbacher98.pdf
[3]. https://en.wikipedia.org/wiki/Optimal_asymmetric_encryption_padding
[4]. https://en.wikipedia.org/wiki/Probabilistic_signature_scheme
[5].PSS Mode of RSA Signature | Develop Paper