Day57【动态规划】647.回文子串、516.最长回文子序列

647.回文子串

力扣题目链接/文章讲解

视频讲解

1、确定 dp 数组下标及值含义

dp[i][j]：表示区间范围为 [i, j] 的子串是否为回文串（j >= i）

这样定义才方便我们的递推！怎么想到的？回文串需要对比串的两端，用二维 dp 数组表示串的两端元素的对比情况 

2、确定递推公式

整体上是两种，就是 s[i] 与 s[j] 相等，s[i] 与 s[j] 不相等这两种

当 s[i] 与 s[j] 不相等，那没啥好说的了，dp[i][j] 一定是 false

当 s[i] == s[j]，有如下三种情况：

1. i == j，此时区间范围 [i, j] 就只有一个元素，当然是回文子串，dp[i][j] 为 true
2. i + 1 = j，此时区间范围 [i, j] 为两个相同元素，也是回文子串，dp[i][j] 也为true
3. i 与 j 相差大于 1 的时候，例如 cabac，此时 s[i] 与 s[j] 已经相同了，我们看区间 [i, j] 是不是回文子串就看区间 [i + 1, j - 1]，即 aba 是不是回文就可以了

上述情况代码如下

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1] == true) { // 情况三
        dp[i][j] = true;
    }
}

3、dp 数组初始化

全部初始化为 false，在遍历填充过程中不断发现回文子串并置 true

4、确定遍历顺序 

根据递推公式看出，dp[i][j] 依赖于其左下方的 dp 值，所以一定要从下到上，从左到右遍历，才能保证 dp[i + 1][j - 1] 都是经过计算的 

5、打印 dp 数组验证

代码如下

class Solution {
public:
    int countSubstrings(string s) {

        vector > dp(s.size(), vector(s.size(), false));

        for (int i = s.size() - 1; i >= 0; --i) {    // 从下往上，从左往右遍历
            for (int j = i; j < s.size(); ++j) {    // 保证j>=i
                if (s[i] == s[j]) {    
                    if (j - i <= 1)
                        dp[i][j] = true;
                    else if (dp[i + 1][j - 1] == true)
                        dp[i][j] = true;
                }
            }
        }

        int res = 0;    // dp[i][j]为true，就表示子串[i, j]为回文子串，统计dp数组中true的数量即可统计出回文子串的数量
        for (const auto & line : dp)
            for (const auto item : line)
                if (item == true)
                    ++res;
        
        return res;
    }
};

516.最长回文子序列 

力扣题目链接/文章讲解

视频讲解

1、定义 dp 数组下标及值含义

dp[i][j]：表示字符串 s 在 [i, j] 范围内的最长回文子序列的长度为 dp[i][j]（j >= i）

回文序列需要对比序列的两端，用二维 dp 数组表示两端元素的对比情况

2、确定递推公式

关键逻辑就是看 s[i] 与 s[j] 是否相同

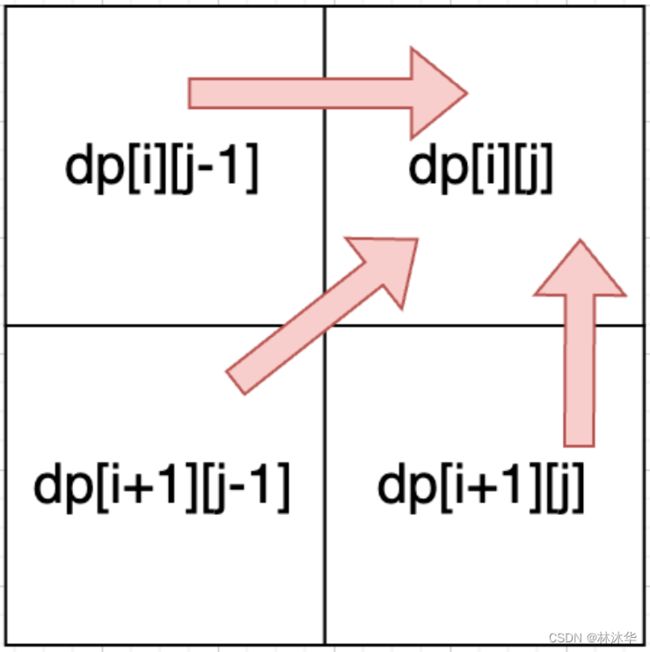
如果 s[i] == s[j]，那么 dp[i][j] = dp[i + 1][j - 1] + 2

如果 s[i] != s[j]，则 s[i, j] 的最长回文子序列不可能同时包含 s[i] 和 s[j]，那么，长度一定为下面两种情况之一

• 只考虑在 s[i, j - 1] 中寻找最长回文子序列，这样能够保证找到的回文子序列不可能同时包含 s[i] 和 s[j]
• 同理，也可以只考虑在 s[i + 1, j] 中找最长回文子序列，这样也能保证找到的回文子序列不可能同时包含 s[i] 和 s[j]

因为找的“最长”回文子序列，上面两种情况取一个最大值，如图 

3、dp 数组初始化

感觉代码随想录讲得不够清晰，我们来逐步推导确定有哪些部分我们需要初始化，以及应该初始化为多少

根据定义我们看出，dp[i][j]：表示字符串 s 在 [i, j] 范围内的最长回文子序列的长度，其中 j >= i

那么，最终我们的 dp 数组也只需要去遍历填充 j >= i 的部分，因为其他部分没有意义

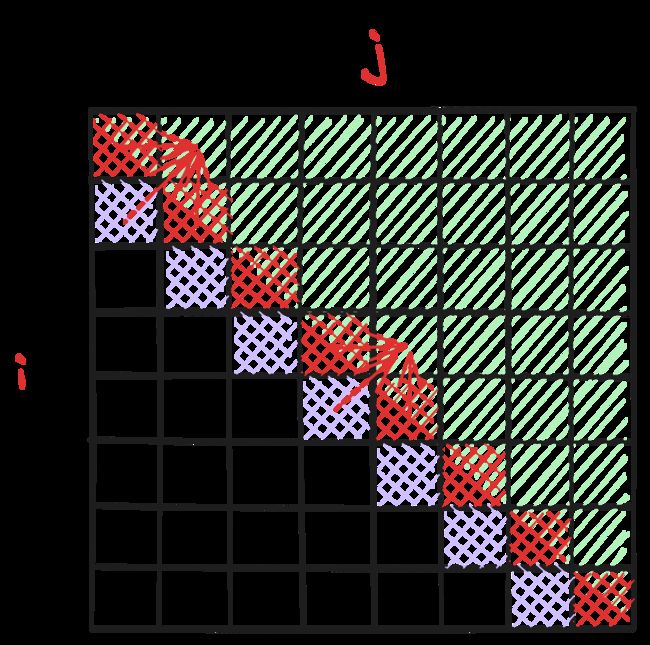
又根据递推公式看出，我们想要推导 dp[i. j]， 需要依赖于其左方、下方、左下方的 dp 值

因此，为了能够遍历填充满绿色部分，我们需要初始化红色对角线部分与紫色部分的值，如下图所示 

对角线红色部分的 dp[i][j]：当 i 与 j 相同，那么 dp[i][j] 一定是等于 1 的，即：一个字符的回文子序列长度就是 1

紫色部分的 dp[i][j]：没有意义。对于这种没有实际意义的不知道如何初始化的，可以根据递推公式判断应该初始化为多少 

哪里用到了紫色部分的值？看图，当 j = i + 1 时，如果 s[i] == s[j]，那么 dp[i][j] = dp[i + 1][j - 1] + 2，这个时候会用到紫色部分的 dp 值。显然，当 j = i + 1 且 s[i] == s[j] 时，即：两个相同字符构成串的最长回文子序长度就是 2，再带回递推公式，可以看出紫色部分应该初始化为 0

其他部分随意初始化，反正会被覆盖

4、确定遍历顺序

从下往上遍历 i，从左往右遍历 j，这样才能保证 dp[i][j] 所依赖的数据是被更新后的正确 dp 值

5、打印 dp 数组验证

代码如下

class Solution {
public:
    int longestPalindromeSubseq(string s) {

        vector > dp(s.size(), vector(s.size(), 123));  // 这里初始化为123表示“其他部分可以随意初始化”

        for (int i = 0; i < s.size(); ++i) {    // 初始化对角线
            dp[i][i] = 1;
        }

        for (int i = 1; i < s.size(); ++i) {    // 初始化紫色部分
            dp[i][i - 1] = 0;
        }

        for (int i = s.size() - 2; i >= 0; --i) // 从下往上，从左往右遍历填充
            for (int j = i + 1; j < s.size(); ++j) {    // 仅需填充未被初始化的部分，看图
                if (s[i] == s[j])
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                else
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
            }

        return dp[0][s.size() - 1]; // 表示字符串s在[0, s.size()-1]范围内的最长回文子序列的长度
    }
};

---

回顾总结 

动态规划结束，定义 dp 数组和递推是关键

动态规划五部曲贯穿始终 

1. 确定 dp 数组下标及值的含义
2. 确定递推公式
3. dp 数组如何初始化
4. 确定遍历顺序
5. 打印 dp 数组验证