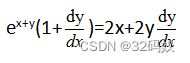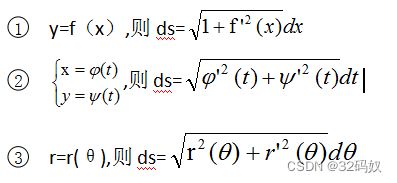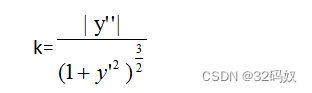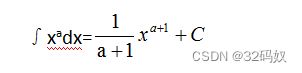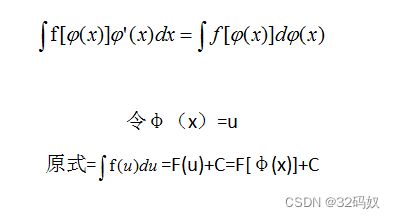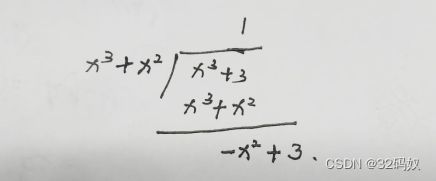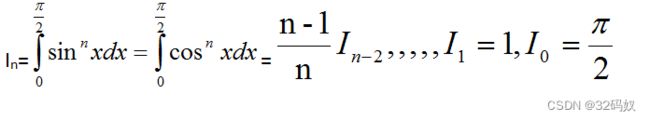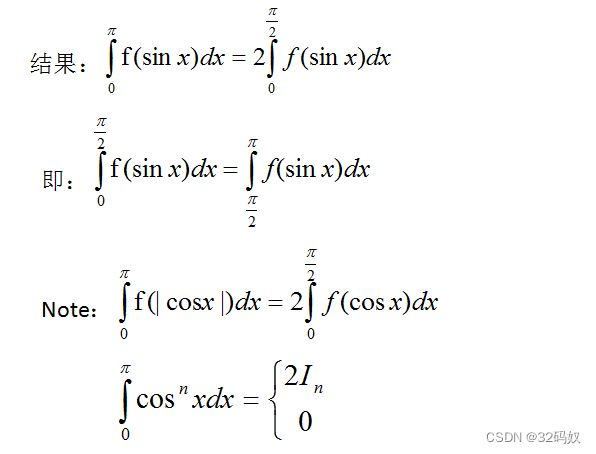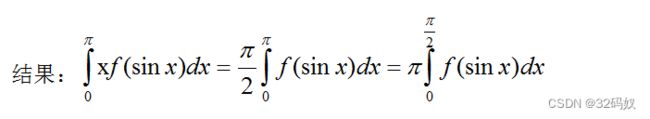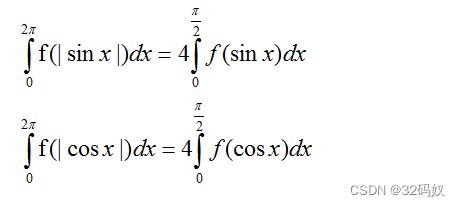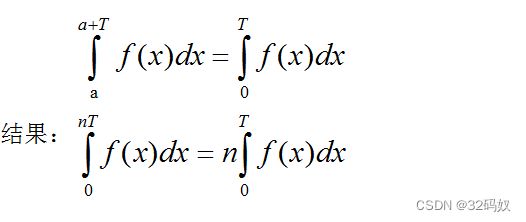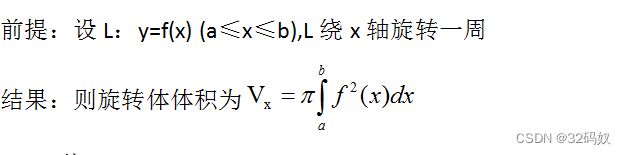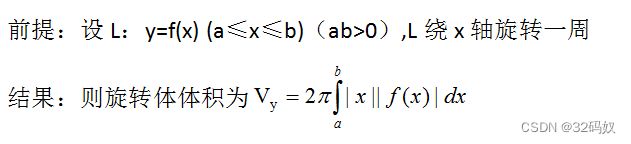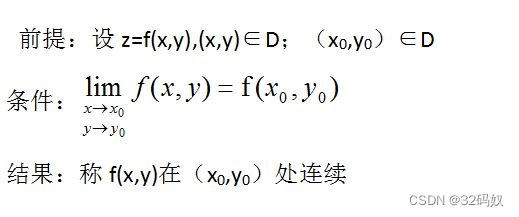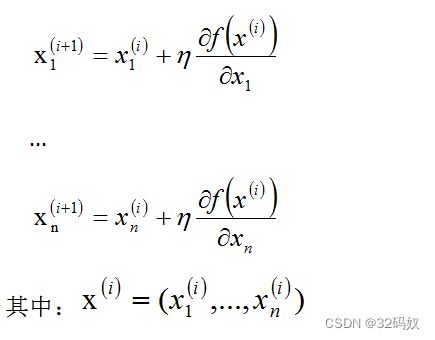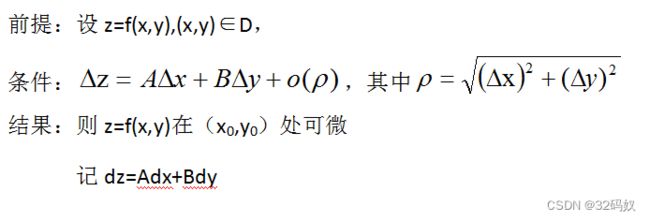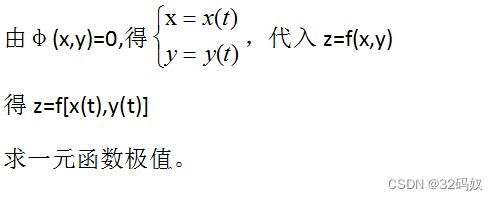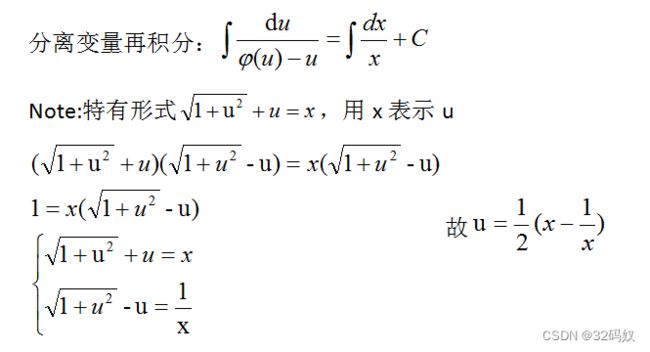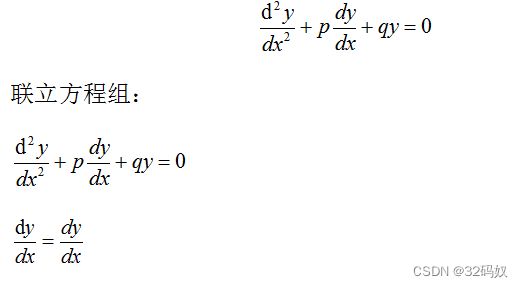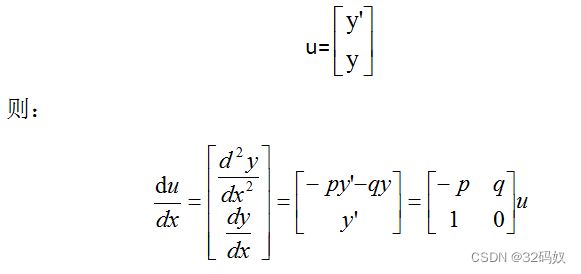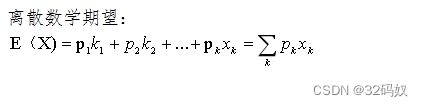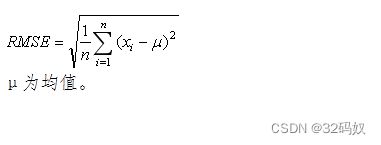数学上的一些知识
文章目录
- 0 导论
-
- 0.1 常用公式
-
- 0.1.1 三次方
- 0.2 数学符号
- 0.3 函数
-
- 0.3.1 指数函数
- 0.3.2 对数函数
- 0.3.3 正弦函数
- 0.4 参数方程
- 0.5 单位转换
- 0.6迪拉克函数
- 1、极限
-
- 1.1 定义
-
- 1.1.1 数列极限(ε—N)
- 1.1.2 函数极限(ε-δ)
- 1.1.3无穷极限(ε-X)
- 1.1.4无穷小
- 1.2.极限的性质
-
- 1.2.1保号性
- 1.2.2有界性
- 1.3.极限的运算性质
- 1.4.极限存在定理
-
- 1.4.1夹逼定理
- 1.4.2 单调有界必有极限
- 1.5 无穷小的性质
- 1.6 连续与间断
-
- 1.6.1 连续
-
- 1.6.1.1 在一点连续
- 1.6.1.2 在一段连续
- 1.6.2 间断
-
- 1.6.2.1 第一类间断
- 1.6.2.2可去间断
- 1.6.2.3跳跃间断
- 1.6.2.4第二类间断
- 2 导数
-
- 2.1 导数定义
- 2.2导数基本公式
-
- 2.2.1幂指对三反三特殊
- 2.2.2复合函数求导
- 2.2.3 反函数求导
- 2.2.4 隐函数求导
- 2.2.5 参数方程求导
- 2.2.6 分段函数求导
- 2.2.7 高阶求导
- 3. 微分
-
- 3.1中值定理
-
- 3.1.1 罗尔中值定理
- 3.1.2 拉格朗日中值定理
- 3.1.3柯西中值定理
- 3.1.4泰勒中值定理
- 3.2 单调性
- 3.3极值的判定
-
- 3.3.1第一充分条件
- 3.3.2第二充分条件
- 3.3.3泰勒公式判别法
- 3.4凹凸性与拐点的判别
- 3.5渐近线
-
- 3.5.1 水平渐近线
- 3.5.2 铅直渐近线
- 3.5.3 斜渐近线
- 3.6弧微分,曲率,曲率半径
- 4.不定积分
-
- 4.1定义
- 4.2常见的不定积分
-
- 4.2.1 幂
- 4.2.2指
- 4.2.3 三
- 4.2.4 反三
- 4.3不定积分的计算
-
- 4.3.1、换元法
- 4.3.2、三角代换
- 4.3.3、倒代换
- 4.3.4、分部积分法
- 4.3.5、有理函数积分
- 5.定积分
-
- 5.1 定义
- 5.2 基本性质
- 5.3.基本原理
-
- 5.3.1定理
-
- 5.3.1.1积分导数定理
- 5.3.1.2牛顿-莱布尼兹公式
- 5.3.1.3积分区间对称性
- 5.3.1.4 定积分存在定理
- 5.3.2三角函数积分性质
- 5.3.3 周期函数积分性质
- 5.4.定积分的计算
-
- 5.4.1换元积分法
- 5.4.2分部积分法
- 5.5 广义积分
-
- 5.5.1区间无限
-
- 5.5.1.1 f(x)在[a,+∞)上连续
- 5.5.1.2 f(x)在(-∞,a]上连续
- 5.5.1.3 f(x)在(-∞,+∞)上连续
- 5.5.2区间有限的无界函数
-
- 5.5.2.1 f(x)在(a,b]上连续,f(x)在x=a的右邻域内无界
- 5.5.2.2 f(x)在[a,b)上连续,f(x)在x=b的左邻域内无界
- 5.5.2.3 f(x)在[a,c)U(c,b]上连续,在x=c的去心邻域内无界
- 5.6.定积分的应用
-
- 5.6.1面积
- 5.6.2体积
- 5.6.3曲线长
- 6.多元函数微分学
-
- 6.1多元函数极限
- 6.2多元函数连续
- 6.3偏导数及其求法
-
- 6.3.1梯度
- 6.3.2 梯度下降法
- 6.4全微分
- 6.5连续、可偏导、可全微的关系
- 6.6求偏导类型
-
- 6.6.1显函数求偏导
- 6.6.2复合函数求偏导
- 6.6.3隐函数求偏导
- 6.7无条件极值与条件极值
-
- 6.7.1二元函数极值定义
- 6.7.2二元函数无条件极值步骤
- 6.7.3二元函数有条件极值步骤
- 7.微分方程
-
- 7.0定义
- 7.1一阶微分方程
-
- 7.1.1可分离变量的微分方程
- 7.1.2齐次微分方程
- 7.1.3一阶齐次线性微分方程
- 7.1.4一阶非齐次线性微分方程
- 7.1.5伯努利方程
- 7.1.6全微分方程
- 7.2可降阶的高阶微分方程
-
- 7.2.1 n阶型
- 7.2.2 缺y型
- 7.2.3缺x型
- 7.3高阶微分方程
-
- 7.3.1n阶齐次线性微分方程
- 7.3.2n阶非齐次线性微分方程
- 7.3.3高阶线性微分方程解的结构
- 7.3.4二阶常系数齐次线性微分方程的解
- 7.3.5二阶常系数非齐次线性微分方程的特解
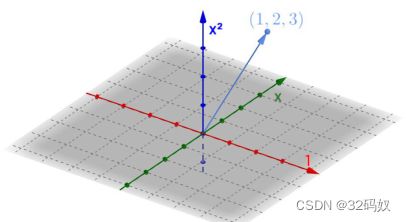
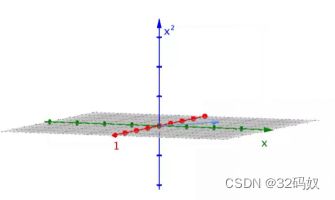
- 7.4不一样的向量
-
- 7.4.1线性变换
- 7.4.2微分算子D的线性
- 7.4.3线性微分方程
- 7.5用矩阵求解二阶齐次线性微分方程
- 极值
-
- 4.极限存在定理
- 5.极限计算
- 向量
-
- 内积
- 期望
- 泰勒展开
- 欧拉公式
- 误差
-
- 均方根误差
- 标准差
- 矩阵论
-
- 行列式
- 逆矩阵
- 伴随矩阵
- 共轭矩阵
- 正交矩阵
- 实对称矩阵
- 复变函数基础
-
- 复数乘除
- Arg 复数的辐角
- 范数
0 导论
0.1 常用公式
0.1.1 三次方
( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 a b + 2 b c + 2 c a (a+b+c)^2 = a^2+b^2+c^2+2ab+2bc+2ca (a+b+c)2=a2+b2+c2+2ab+2bc+2ca
0.2 数学符号
- Z:全体整数
- N+:正整数
- N:自然数,非负整数
- R:实数
- C:复数
- Q:有理数
- D是特定的集合
- argmin:使后面的式子达到最小值的x的取值,若cosx在π处取得最小值,则argmin(cosx)=π
- sup:上界.
- Σ,for循环
- 双Σ,双for循环
0.3 函数
幂指对正余弦 反三角
0.3.1 指数函数
指数函数随着x的增大,值得增长是所有函数中最快的,即指数增长。
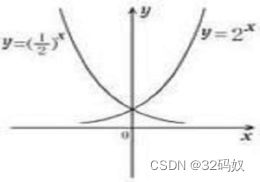
0.3.2 对数函数
运算: lna+lnb=lnab
a 3 = e 3 l n a a^3 = e^{3lna} a3=e3lna
ln10/9=ln10-ln9
am=N 以a为底N的对数 logaN=m。
始为基,知为果,求为次。
对N取对数,就是说10的几次等于N

将乘除变为指数的加减。取对数可缩小。
超前滞后
0.3.3 正弦函数
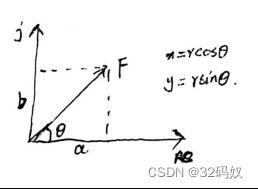
0.4 参数方程
0.5 单位转换
1磅=0.454千克
0.6迪拉克函数
H(x)阶跃函数:
![]()
对阶跃函数取微分可以得到δ函数。事实上对于一个不连续的函数取微分都可以出现δ函数。
δ函数定义:
δ(x)=0,(x≠0)
![]()
1、极限
1.1 定义
数列极限(ε-N)、函数极限(ε-δ)、无穷极限(ε-X)
Limf(x)=A⇔/等价于/充要f(x)=A+α,其中α→0
1.1.1 数列极限(ε—N)
对于任意ε>0,都∃N>0,n>N时,有 ∣ a n − A ∣ < ε |a_n-A|<ε ∣an−A∣<ε,称A为数列{an}的极限,即
![]()
1.1.2 函数极限(ε-δ)
对任意ε>0,都∃δ>0,0<|x-a|<δ时,有|f(x)-A|<ε
称A为函数f(x)当x→a的极限,即
![]()
1.1.3无穷极限(ε-X)
1.对任意ε>0,都∃X>0,x<-X时,有|f(x)-A|<ε
称A为函数f(x)当x→-∞的极限,即
![]()
2.对任意ε>0,都∃X>0,|x|>X时,有|f(x)-A|<ε
称A为函数f(x)当x→+∞的极限,即
![]()
1.1.4无穷小
无穷小是一个向0奔跑的变量
通过研究这种向0奔跑的过程,我们可以得到不同无穷小之间的大小关系。
假如说x→0,y→0
当x=0.1时,y=0.07
当x=0.01时,y=0.005.
说明x和y向0奔跑的速度完全是不同的。x和y的函数关系确定了奔跑速度之间的关系。
高阶无穷小,y从一个足球表明向0趋近,x从一个乒乓球表面向0趋近,且x比y跑得快。x就是y的高阶无穷小
也就是说:
无穷小是一种向0奔跑的变量
不同无穷小之间可以具有函数关系
具有函数关系的两个无穷小,在向0奔跑过程中,它们的大小比例趋于一个极限,这个极限就代表了两个无穷下之间的大小关系。
此时x2,就是x的高阶无穷小,x2的权是1,3x^2的权是3。权和阶可以囊括所有无穷小的特点。同时无穷小的倒数无穷大, 4 / x 2 4/x^2 4/x2就是权为4,阶为2的无穷大。
然后把所有的有限实数表示为0阶的无穷小或无穷大,实数的值代表他们的权值。
形成新的数域:无穷分阶∈。每个数都有权和阶两个属性。所以表示为
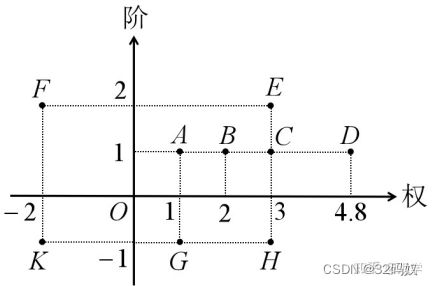
其中A到K都代表无穷分阶数域中的数。上半平面为无穷小,下半平面为无穷大。
用a(0)^b表示,a代表权,b代表阶,b>0时是无穷小,称权为a的b阶无穷小,b<0时是无穷大,在下半平面,称权为a的-b阶无穷大。
用a(∞)^b表示,a代表权,b代表阶,b>0时是无穷大,称权为a的b阶无穷大,b<0时是无穷小,在上半平面,称权为a的-b阶无穷小。
1.2.极限的性质
唯一性、保号性、有界性、列与子列
1.2.1保号性
前提:有>0,
条件:当∃δ>0,使0<|x-a|<δ时
结果:则f(x)>0
1.2.2有界性
- 1.函数局部有界
前提:有

条件:当∃δ>0与M>0,使0<|x-a|<δ时
结果:则|f(x)|≤M - 2.数列有界
前提:有

条件:∃M>0
结果:使|an|≤M
数列收敛则有界,数列有界不一定收敛
1.3.极限的运算性质
1.4.极限存在定理
夹逼、单调有界
1.4.1夹逼定理
函数夹逼定理
前提:f(x)≤g(x)≤h(x)
条件:limf(x)=limh(x)=A
结果:limg(x)=A
1.4.2 单调有界必有极限
1.5 无穷小的性质
(1)有限个无穷小的和、差、积仍是无穷小
(2)无穷小×常数仍是无穷小
(3)有界函数与无穷小之积仍是无穷小
麦克劳林公式


有加有减,有减无减
1.6 连续与间断
1.6.1 连续
1.6.1.1 在一点连续
-
f(x)在x=a处连续 即

-
f(x) 在[a,b]上连续
1.6.1.2 在一段连续
即f(x)在[a,b]内处处连续,同时f(a)=f(a+0),f(b)=f(b-0).
1.6.2 间断
为什么会间断?
因为不存在而间断,如1/x,或tanx的x=0
1.6.2.1 第一类间断
在一点处,左右极限都∃
1.6.2.2可去间断
f(a-0)=f(a+0)≠f(a)
1.6.2.3跳跃间断
f(a-0)≠f(a+0)
1.6.2.4第二类间断
在一点处,左右极限不都∃
2 导数
2.1 导数定义
Δx→0, x → x 0 x→x_0 x→x0
前提:有y=f(x),x∈D,x0∈D,x0+Δx∈D,Δy=f(x0+Δx)-f(x0)
条件:若
或者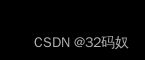 存在
存在
f(x)在x0上的切线方向
结果:y=f(x)在x=x0处可导
导数就是势存在,势的表达形式是极限
-
y=f(x)在x=x0处可导的充要是 f ’ − ( x 0 ) f’_-(x_0) f’−(x0)与 f ’ + ( x 0 ) f’_+(x_0) f’+(x0)都存在
左导数f’-(x0):
-
连续可导
f(x)可导,且f’(x)连续,称之为连续可导 -
可导与连续
可导一定连续,连续不一定可导 -
奇偶性
可导奇函数的导为偶函数
可导偶函数的导为奇函数
另外:可导偶函数的f’(0)=0,因为偶函数关于y轴对称
2.2导数基本公式
2.2.1幂指对三反三特殊
三
( t a n x ) ’ = s e c 2 x (tanx)’=sec^2x (tanx)’=sec2x
( c o t x ) ’ = − c s c 2 x (cotx)’=-csc^2x (cotx)’=−csc2x
(secx)’=tanxsecx
(cscx)’=-cotxcscx
反三

2.2.2复合函数求导
条件:若y=f(x)可导,u=φ(x),φ’(x)≠0
结果:则y=f[φ(x)]可导,![]()
2.2.3 反函数求导
2.2.4 隐函数求导
2.2.5 参数方程求导
2.2.6 分段函数求导
2.2.7 高阶求导
3. 微分
y=f(x)
X 、 x 0 、 x o + Δ x X、x_0、x_o+Δx X、x0、xo+Δx皆属于D(特定的集合)
Δ y = f ( x 0 + Δ x ) − f ( x 0 ) Δy=f(x_0+Δx)-f(x0) Δy=f(x0+Δx)−f(x0)为f(x)在x0处的增量
若Δy=AΔx+o(Δx),称f(x)在 x 0 x_0 x0处可微
AΔx称f(x)在 x 0 x_0 x0处微分
记 d y ∣ x = x 0 = A Δ x dy|_{x=x0}=AΔx dy∣x=x0=AΔx或 d y ∣ x = x 0 = A d x dy|_{x=x0}=Adx dy∣x=x0=Adx
Δy-dy=o(Δx)
- 可导等价于可微
- 可导(可微)必连续
3.1中值定理
3.1.1 罗尔中值定理
前提:f(x)在[a,b]闭内连续,开内可导
条件:若f(a)=f(b)
结果:∃ξ∈开(a,b),使f’(ξ)=0
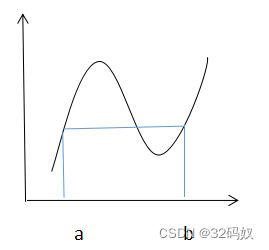
3.1.2 拉格朗日中值定理
前提:f(x)在[a,b]闭内连续,开内可导
结果:∃ξ∈开(a,b),使![]()
证明:设K法,转化为罗尔问题
设![]()
f(b)-f(a)=kb-ka
f(b)-kb=f(a)-ka
设F(x)=f(x)-kx
则F(b)=F(a)
则∃F’(ξ)=0,即f’(ξ)-k=0,即f’(ξ)=k
证得 ![]()
3.1.3柯西中值定理
前提:f(x)与g(x)在[a,b]闭内连续,开内可导
条件:g’(x)≠0(a
证明:设K法,转化为罗尔问题
3.1.4泰勒中值定理
拉格朗日型
前提f(x)在 x = x 0 x=x_0 x=x0的邻域内n+1阶可导

(ξ在x与x0之间)
皮尔诺型

note:泰勒展开揭示了一个函数立于一点预测任何一点的值。
3.2 单调性
定理: 在区间I内,f’>0,则f(x)在区间I内单增
在区间I内,f’<0,则f(x)在区间I内单减
3.3极值的判定
1.求f’(x),求出f(x)的驻点以及不可导点。
2.判别法
3.3.1第一充分条件
① 存在δ>0
② 当x∈( x 0 x_0 x0-δ,x0)时,有f’(x)>0,当 x ∈ ( x 0 , x 0 + δ ) x∈(x_0,x_0 +δ) x∈(x0,x0+δ)时,有f’(x)<0,则 x = x 0 x=x_0 x=x0为f(x)的极大值点。
③ 当 x ∈ ( x 0 − δ , x 0 ) x∈(x_0-δ,x0) x∈(x0−δ,x0)时,有f’(x)<0,当 x ∈ ( x 0 , x 0 + δ ) x∈(x_0,x_0 +δ) x∈(x0,x0+δ)时,有f’(x)>0,则 x = x 0 x=x_0 x=x0为f(x)的极小值点。
一阶势由正变负为极大,一阶势由为负变正为极小
3.3.2第二充分条件
① 函数f(x)在 x = x 0 x=x_0 x=x0处二阶可导,且f’(x)=0,
② F”(x)>0 x = x 0 x=x_0 x=x0为f(x)的极小值点
③ F”(x)<0, x = x 0 x=x_0 x=x0为f(x)的极大值点
一阶势为零,二阶势为增(一阶势由负变正)为极小
一阶势为零,二阶势为减(一阶势由正变负)为极大
3.3.3泰勒公式判别法
3.4凹凸性与拐点的判别
判别法:
当x∈I时,f’’>0,则y=f(x)为凹函数
当x∈I时,f’’<0,则y=f(x)为凸函数
- 拐点
在区间I上,若f(x)在 x = x 0 x=x_0 x=x0两侧的凹凸性不同,则 x = x 0 x=x_0 x=x0处有曲线f(x)的拐点.
判别法:
条件:若f(x)三阶可导,f’’(x0)=0,但f’’’(x0)≠0
结果:则x=x0处有曲线f(x)的拐点.
3.5渐近线
3.5.1 水平渐近线
结果:称y=A 为f(x)的水平渐近线
3.5.2 铅直渐近线
条件;若![]() 或f(a-0)=∞,或f(a+0)=∞
或f(a-0)=∞,或f(a+0)=∞
结果:称x=a 为f(x)的铅直渐近线
3.5.3 斜渐近线
3.6弧微分,曲率,曲率半径
曲率半径公式
R=1/k
4.不定积分
4.1定义
不定积分是一种操作结果
条件:若F(x)为f(x)的原函数
结果:则f(x)的所有原函数F(x)+C为f(x)的不定积分
即∫f(x)dx=F(x)+C
4.2常见的不定积分
幂指对三反三
4.2.1 幂
4.2.2指
4.2.3 三
∫ cosx dx = sinx + C
∫ sinx dx = - cosx + C
∫ cotx dx = ln|sinx| + C
∫ tanx dx = - ln|cosx| + C
∫ secx dx =ln|secx + tanx| + C
∫ cscx dx =ln|cscx - cotx| + C
∫ sec^(2)x dx = tanx + C
∫ csc²x dx = - cotx + C
∫ secxtanx dx = secx + C
∫ cscxcotx dx = - cscx + C
4.2.4 反三
4.3不定积分的计算
4.3.1、换元法
4.3.2、三角代换
4.3.3、倒代换
4.3.4、分部积分法
条件:若u(x),v(x)连续可导
结果:则∫udv=uv-∫vdu
推导: (uv)‘=u’v+uv’ 故u’v=(uv)‘-uv’
两边积分得:∫ u’v dx=∫ (uv)’ dx - ∫ uv’ dx
即:∫udv=uv-∫vdu,这就是分部积分公式
4.3.5、有理函数积分
有理函数R:R(x)=![]() ,其中P、Q为多项式
,其中P、Q为多项式
真分式——将R(x)拆成两部分和
(1)![]()

5.定积分
5.1 定义
前提:y=f(x)在[a,b]有界
化整为零: a = x 0 < x 1 < . . . < x n = b a=x_0
[ a , b ] = [ x 0 , x 1 ] U [ x 1 , x 2 ] U . . . U [ x n − 1 , x n ] [a,b]=[x_0,x_1]U[x_1,x_2]U...U[x_{n-1},x_n] [a,b]=[x0,x1]U[x1,x2]U...U[xn−1,xn]
1 ≤ i ≤ n , Δ x i = x i − x i − 1 , ξ i ∈ [ x i − 1 , x i ] , s i = f ( ξ i ) Δ x i 1≤i≤n , Δx_i=x_i-x_{i-1} , ξ_i∈[x_{i-1}, x_i] , s_i=f(ξ_i)Δx_i 1≤i≤n,Δxi=xi−xi−1,ξi∈[xi−1,xi],si=f(ξi)Δxi
积零为整:取λ=![]() ,若
,若 ∃
∃
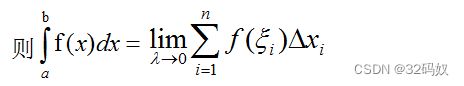
5.2 基本性质
4)有界不等式,若f(x)在[a,b]上,m≤f(x)≤M,则
![]()
5)积分中值定理
条件:若f(x)在[a,b]闭内连续
结果:则∃ξ∈[a,b],使

5.3.基本原理
5.3.1定理
5.3.1.1积分导数定理
条件:设f(x)在[a,b]闭内连续,令
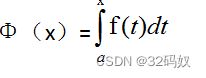
结果:Φ’(x)=f(X)
注
故
5.3.1.2牛顿-莱布尼兹公式
f(x)在[a,b]内连续,F(x)是f(x)的一个原函数,则

5.3.1.3积分区间对称性
5.3.1.4 定积分存在定理
区间有限,函数有界
5.3.2三角函数积分性质
5.3.3 周期函数积分性质
5.4.定积分的计算
5.4.1换元积分法
条件:f(x)在[a,b]连续,令x=φ(t),φ(α)=a
结果:

5.4.2分部积分法
条件:有u(x),v(x),在[a,b]上连续可导
结果:则

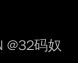
5.5 广义积分
5.5.1区间无限
5.5.1.1 f(x)在[a,+∞)上连续
5.5.1.2 f(x)在(-∞,a]上连续
条件:若![]() 存在,且=A,
存在,且=A,
结果:则 收敛,且=A
收敛,且=A
极限判别法:
条件:若![]() ,且k>1
,且k>1
结果:则 收敛
收敛
条件:若![]() ,且k≤1,或者M>0
,且k≤1,或者M>0
结果:则 发散
发散
5.5.1.3 f(x)在(-∞,+∞)上连续
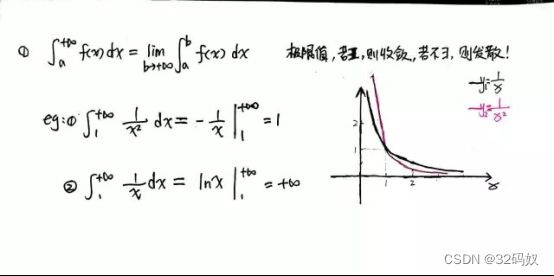
当x→±∞时,k>1,则原函数如1/(x^2)收敛
当x→某个数时,k≤1,则原函数如(1/x)收敛
如: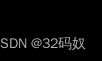 求解
求解

note:由于±无穷区间并不是严格对称的,因为∞+1=∞
5.5.2区间有限的无界函数
5.5.2.1 f(x)在(a,b]上连续,f(x)在x=a的右邻域内无界
定义:
前提:对于任意ε>0,有
条件:若![]() 存在,且=A
存在,且=A
结果:则称广义积分 收敛,且=A
收敛,且=A
极限判别法:
条件:若![]() ,且k<1
,且k<1
结果:则 收敛
收敛
条件:若![]() ,且k≥1
,且k≥1
结果:则 发散
发散
5.5.2.2 f(x)在[a,b)上连续,f(x)在x=b的左邻域内无界
5.5.2.3 f(x)在[a,c)U(c,b]上连续,在x=c的去心邻域内无界
![]()
5.6.定积分的应用
5.6.1面积
元素法
(1)极坐标面积
![]()
5.6.2体积
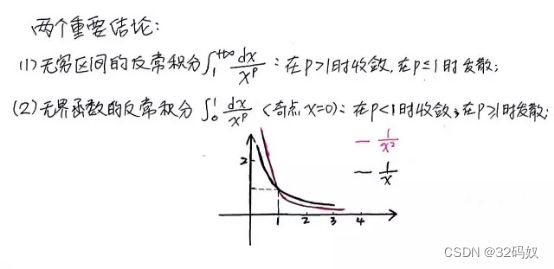
5.6.3曲线长
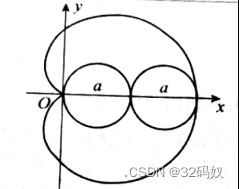
6.4常见特殊曲线
① 圆一
直角坐标:
![]()
③ 圆三
直角坐标:x²+y²=2Ry
极坐标:r=2Rsinθ
④ 摆线
参数方程:

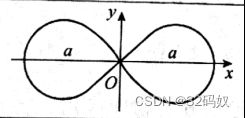
⑥ 双妞线
直角坐标:(x²+y²)²=a²(x²-y²)
极坐标:r²=a²cos2θ
6.多元函数微分学
6.1多元函数极限
6.2多元函数连续
6.3偏导数及其求法
6.3.1梯度
对于多元函数f(X)=f(x1,…,xn)来说,它们的偏导数就是梯度
![]()
多元函数f(x)在x0处的泰勒级数是:

6.3.2 梯度下降法
从数学上来说,梯度方向是函数增长速度最快的方向。
因此,梯度的反方向就是函数减少最快的方向
假设,希望求解的目标函数f(X)=f(x1,…,xn)的最小值
一个初始点![]()
,对于x1的全部迭代,i变动
…
一旦达到收敛条件,迭代就结束。
有可能lim(i→∞)使函数值→0.
反之,如果要求最大值,就沿着梯度的反方向前进。
无论计算最大还是最小,都需要构建一个迭代关系:
对于所有的i,都满足 x i + 1 = g ( x i ) x^{i+1}=g(x^i) xi+1=g(xi)
函数g可以表达为

6.4全微分
6.5连续、可偏导、可全微的关系
定理一:若函数f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处可微,则该点处既连连续又可偏导,反之不对。
定理二:若f(x,y)两个偏导数连续,则f(x,y)一定可微,反之不对
定理三:若f(x,y)具有二阶连续的偏导数,则 f ’ ’ x y = f ’ ’ y x ( x , y ) f’’_{xy}=f’’_{yx}(x,y) f’’xy=f’’yx(x,y)
6.6求偏导类型
6.6.1显函数求偏导
显函数求偏导即z=f(x,y)对x,y求偏导
对x求偏导时,只需要将y看成常数,![]()
6.6.2复合函数求偏导
6.6.3隐函数求偏导
1.一个约束的情形:
前提:设F(x,y,z)=0在![]() 的邻域内连续可偏导。
的邻域内连续可偏导。
由F(x,y,z)=0可唯一确定具有具有连续偏导数的二元函数z=f(x,y)

6.7无条件极值与条件极值
6.7.1二元函数极值定义
对于二元函数z=f(x,y);
设 ( x , y ) ∈ D ,( x 0 , y 0 ) ∈ D (x,y)∈D ,(x_0,y_0)∈D (x,y)∈D,(x0,y0)∈D,
若∃δ>0,当0<![]() <δ时,有 f ( x , y ) < f ( x 0 , y 0 ) f(x,y)
<δ时,有 f ( x , y ) < f ( x 0 , y 0 ) f(x,y)
称点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)为z=f(x,y)的极大值点, f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0)称函数f(x,y)的极大值
极小值同理
6.7.2二元函数无条件极值步骤
6.7.3二元函数有条件极值步骤
对二元函数z=f(x,y),在约束条件(第三条件)φ(x,y)=0下的极值
求出(x,y)的值,确定最优解。
7.微分方程
7.0定义
微分方程:含有导数或微分的方程
微分方程阶数:导数或微分的最高阶
微分方程的解:使微分方程成立的函数
特解:不含任意常数的解
通解:常数个数与阶数相等的解
线性:符合可加性与齐次性的变换

Note:也可以用y=f(ax)=af(x)来表示齐次。幂指对皆为齐次。
非齐次:Q(x) 为y的零次
Note:
齐次坐标:如果一个二维点(x,y)与形如(kx,ky,k)的所有三元坐标都是等价的
它们就是这个坐标的齐次坐标
将齐次坐标,除以第三个数就可以得到原始二维坐标
但,注意K≠0,(x,y,0)表示∞远
线性变换:
通常用一个矩阵来表示线性变换
即将直线上的点(向量)变换到另一根直线上去
相反,角,长度,则都不能维持原样
7.1一阶微分方程
7.1.1可分离变量的微分方程
7.1.2齐次微分方程
7.1.3一阶齐次线性微分方程
7.1.4一阶非齐次线性微分方程
7.1.5伯努利方程
7.1.6全微分方程
7.2可降阶的高阶微分方程
7.2.1 n阶型
n阶微分方程: y ( n ) = f ( x ) y^{(n)}=f(x) y(n)=f(x)
解法:n次积分
7.2.2 缺y型
7.2.3缺x型
7.3高阶微分方程
7.3.1n阶齐次线性微分方程
7.3.2n阶非齐次线性微分方程
7.3.3高阶线性微分方程解的结构
7.3.4二阶常系数齐次线性微分方程的解
二级常系数齐次线性微分方程:y’’+py’+qy=0
求解特征方程:λ²+pλ+q=0
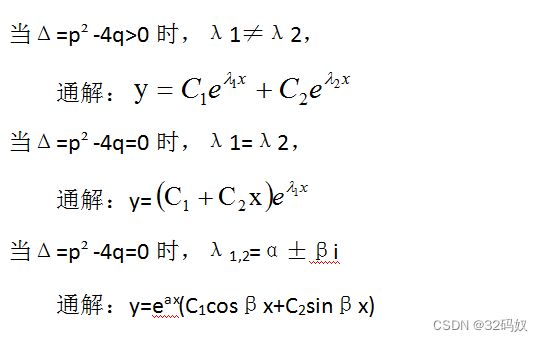
7.3.5二阶常系数非齐次线性微分方程的特解
二级常系数非齐次线性微分方程:y’’+py’+qy=f(x)
- 当 f ( x ) = e a x [ P ( x ) c o s β x + P ’ ( x ) s i n β x ] f(x)=e^{ax}[P(x)cosβx+P’(x)sinβx] f(x)=eax[P(x)cosβx+P’(x)sinβx]
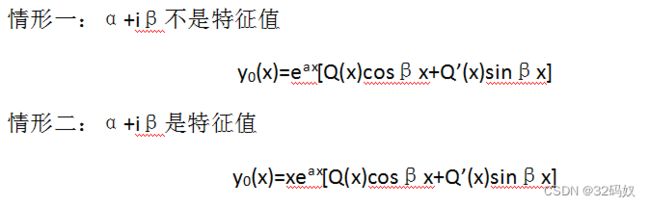
Note:按右边的形式假设,正弦余弦都有,多项式以最高次为准
如: y ’’ − 2 y ’ + 2 y = x e x c o s x y’’-2y’+2y=xe^xcosx y’’−2y’+2y=xexcosx
特征方程:λ²-2λ+2=0 解得: λ 1 , 2 = 1 ± i λ_{1,2}=1±i λ1,2=1±i ,而α=1,β=1
设: y 0 ( x ) = x e x [ ( a x + b ) c o s x + ( c x + d ) s i n x ] y_0(x)=xe^x[(ax+b)cosx+(cx+d)sinx] y0(x)=xex[(ax+b)cosx+(cx+d)sinx]
7.4不一样的向量
7.4.1线性变换
线性变换的代数定义:
数学中,只要符合下面两个性质的就是线性变换(T代表变换)
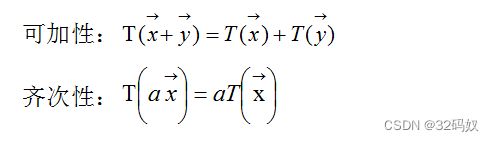
Note:线性变换就是对一个向量的旋转、缩放、斜切;
Note:线性变换后,原本一条直线上等距的点仍然在同一直线且等距;所有起点位于原点的向量经过变换后起点仍然位于原点。(平移不是线性变换。)
如:两个多项式函数 f(x)=1+2x+3x² g(x)=2+3x+4x²
验证:
可加性:D(f(x)+g(x))=D(f(x))+D(g(x))=5+14x
齐次性:D(af(x))=aD(f(x)=a(2+6x)
故:D为线性变换
同时,D的多项式组合 a D + b D 2 + c D n aD+bD²+cD^n aD+bD2+cDn也是线性变换
7.4.2微分算子D的线性
此时D也是一个线性变换
7.4.3线性微分方程
设:L为D的多项式组合,L 为线性变换
L=![]()
定义线性微分方程: L(y)=f(x)
当f(x)=0时,为齐次线性微分方程: L(y)=0
根据特征值和特征向量的定义,当L=D有:

同理:对于L=D²-2D-8

7.5用矩阵求解二阶齐次线性微分方程
对于一个一阶齐次线性微分方程:y’+ky=0
定义:S=D+kI ,D为微分算子——求导,I为单位算子——不变
则: S(y)=(D+kI)(y)=y’+ky
二阶微分方程可以看做零个一阶算子S相乘的结果, s ( 2 ) = s × s s^{(2)}=s×s s(2)=s×s
即:

![]()
7.重积分
7.1二重积分定义
曲顶柱体如下图所示
曲顶柱体的俯视图如下
dσ条的体积示意图:
dσ片的体积:
固定x,体积为: ∫f(x,y)dσ
重新在x维度上积分:
Note:其中z=f(x,y)是曲顶的坐标,同时也是曲顶柱体的高;
Note:曲顶柱体是曲顶在x-y平面上的投影
7.2二重积分性质
1.普通对称性 D区域关于y轴对称.
Note:底面积相同,高相等或相反(将x,y与-x,y代入z=f(x,y)内,相等即两倍,相反即为)
2.D区域关于x轴对称
例子:
正方形为区域D,|x|≤1,|y|≤1
分为四个区域Dk(k=1.2.3.4)
问:中Ik的最大值为?
对于D1, y始终为正,则yexs始终为正,则I1始终为正
对于D2,为0
对于D3,y始终为负
对于D4,为0
2.轮换对称性
引子:
(1)
是否相等?依然相等
积分值与用何字母无关
x,y只是一个衡量符号(仅仅改变了x、y轴的位置)
(2)
巧合:区域D依然不变,即关于y=x对称
定义:若将D中的x、y对调,发现D不变
则
例子应用:D={(x,y)|x²+y²≤1,x≥0,y≥0}
算:I=
轮换I=
故2I=∬(a+b)dxdy
7.二重积分计算
7.4二重积分应用
极值
判别法:
一. 一阶导数为0,二阶导数大于零为极小。
一阶导数为0,二阶导数小于零为极大。
二. 存在δ>0
当x∈(x0-δ,x0)时,有f’(x)>0,当x∈(x0,x0 +δ)时,有f’(x)<0,则x=x0为f(x)的极大值点。
当x∈(x0-δ,x0)时,有f’(x)<0,当x∈(x0,x0 +δ)时,有f’(x)>0,则x=x0为f(x)的极小值点。
一阶导由正变负为极大,一阶导由为负变正为极小
4.极限存在定理
5.极限计算
常用的等价无穷小
![]()
向量
内积
内积:先模投影,再模相乘,(x,y)=|y||x|cos
期望
泰勒展开
欧拉公式
误差
均方根误差
标准差
正态分布
高斯白噪声指的是概率密度函数服从正态分布的噪声,高斯分布。记为N(μ,σ²),μ为数学期望,σ²为方差,σ²=1时称为标准正态分布。
高斯分布的一维概率密度:

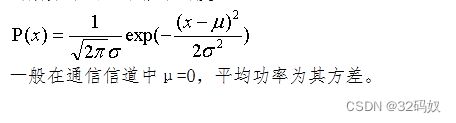
分布图
矩阵论
行列式
对调矩阵的两行不变;——行列式变负
矩阵的某行乘以非零常数k不变;——行列式行列提取
矩阵某行的f(λ)倍加到另一行; ——行列式子相同
逆矩阵
伴随矩阵
adj(A)
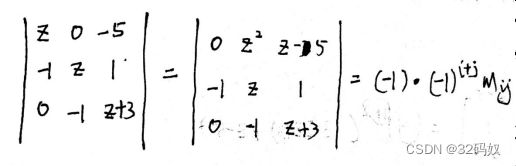
余子式:在行列式|A|中去掉第i行和第j列、余下元素记为Mij,称Mij为元素aij的余子式。
代数余子式: A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij称元素 a i j a_{ij} aij的代数余子式。
记伴随矩阵:
共轭矩阵
实部相等,虚部互为相反数。
正交矩阵
设Q为n阶矩阵,若QTQ=E,称Q为正交矩阵;正交矩阵性质:若Q为正交矩阵,QT=Q-1,Q的转置等于Q的逆
实对称矩阵
A的转置等于A
a. A的特征值都是实数
b. 不同特征值对应的特征向量正交
c. 一定可以相似对角化
Hermit矩阵:A^H=A,A为n*n的矩阵
复变函数基础
复数乘除
Arg 复数的辐角
θ是F的辐角,记为θ=arg(F),F=r(cosθ+jsinθ)