牛客面试高频算法题js(输出二叉树的右视图、岛屿数量、矩阵的最小路径和、字符串出现次数的TopK问题、二叉树根节点到叶子节点的所有路径和)
NC136 输出二叉树的右视图
描述
请根据二叉树的前序遍历,中序遍历恢复二叉树,并打印出二叉树的右视图
数据范围: 0 \le n \le 100000≤n≤10000
要求: 空间复杂度 O(n)O(n),时间复杂度 O(n)O(n)
如输入[1,2,4,5,3],[4,2,5,1,3]时,通过前序遍历的结果[1,2,4,5,3]和中序遍历的结果[4,2,5,1,3]可重建出以下二叉树:
所以对应的输出为[1,3,5]。
示例1
输入:
[1,2,4,5,3],[4,2,5,1,3]
返回值:
[1,3,5]
备注:
二叉树每个节点的值在区间[1,10000]内,且保证每个节点的值互不相同。
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* 求二叉树的右视图
* @param xianxu int整型一维数组 先序遍历
* @param zhongxu int整型一维数组 中序遍历
* @return int整型一维数组
*/
function solve( xianxu , zhongxu ) {
// 利用前序遍历和中序遍历的数组创建树(递归)
function buildTree(xianxu,zhongxu ){
if(xianxu.length==0||zhongxu.length==0){
return null;
}
let tree={
val:xianxu[0],
left:null,
right:null,
}
// 寻找中序遍历中的跟节点
let index=zhongxu.indexOf(xianxu[0]);
// 递归构建左右子树
tree.left=buildTree(xianxu.slice(1,index+1),zhongxu.slice(0,index));
tree.right=buildTree(xianxu.slice(index+1,xianxu.length),zhongxu.slice(index+1,zhongxu.length))
return tree;
}
let tree=buildTree(xianxu,zhongxu);
let res=[];
let p=[];
let x=[];
p.push(tree);
// res.push(tree.val)
// 层序遍历,每次循环p中最后一个节点为每层树最右边的节点
while(p.length!=0){
let len=p.length;
for(let i=0;i<len;i++){
let node = p.shift();
// 当i循环至最后,将节点值推入数组中
if(i==len-1)
res.push(node.val);
if(node.left){
p.push(node.left);
}
if(node.right){
p.push(node.right);
}
}
}
return res;
}
module.exports = {
solve : solve
};
NC109 岛屿数量
描述
给一个01矩阵,1代表是陆地,0代表海洋, 如果两个1相邻,那么这两个1属于同一个岛。我们只考虑上下左右为相邻。
岛屿: 相邻陆地可以组成一个岛屿(相邻:上下左右) 判断岛屿个数。
例如:
输入
[
[1,1,0,0,0],
[0,1,0,1,1],
[0,0,0,1,1],
[0,0,0,0,0],
[0,0,1,1,1]
]
对应的输出为3
(注:存储的01数据其实是字符’0’,‘1’)
示例1
输入:
[[1,1,0,0,0],[0,1,0,1,1],[0,0,0,1,1],[0,0,0,0,0],[0,0,1,1,1]]
返回值:
3
示例2
输入:
[[0]]
返回值:
0
示例3
输入:
[[1,1],[1,1]]
返回值:
1
备注:
01矩阵范围<=200*200
思路:
深度优先搜索(dfs) 深度优先搜索一般用于树或者图的遍历,其他有分支的(如二维矩阵)也适用。它的原理是从初始点开始,一直沿着同一个分支遍历,直到该分支结束,然后回溯到上一级继续沿着一个分支走到底,如此往复,直到所有的节点都有被访问到。
step 1:优先判断空矩阵等情况。
step 2:从上到下从左到右遍历矩阵每一个位置的元素,如果该元素值为1,统计岛屿数量。
step 3:接着将该位置的1改为0,然后使用dfs判断四个方向是否为1,分别进入4个分支继续修改。
代码:
/**
* 判断岛屿数量
* @param grid string字符串型二维数组
* @return int整型
*/
function solve( grid ) {
let n=grid.length;
let m=grid[0].length;
// 递归节点并置0,当该节点四周有节点为1,则继续递归
function dfs(grid,i,j){
grid[i][j]="0";
// 左
if(i-1>=0&&grid[i-1][j]=="1"){
dfs(grid,i-1,j)
}
// 上
if(j-1>=0&&grid[i][j-1]=="1"){
dfs(grid,i,j-1)
}
// 右
if(i+1<n&&grid[i+1][j]=="1"){
dfs(grid,i+1,j)
}
// 下
if(j+1<m&&grid[i][j+1]=="1"){
dfs(grid,i,j+1)
}
}
let count=0;
for(let i=0;i<n;i++){
for(let j=0;j<m;j++){
// 遍历每一个节点
if(grid[i][j]=="1"){
count++;
dfs(grid,i,j);
}
}
}
return count;
}
module.exports = {
solve : solve
};
NC59 矩阵的最小路径和
描述
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
数据范围: 1 \le n,m\le 5001≤n,m≤500,矩阵中任意值都满足 0 \le a_{i,j} \le 1000≤a**i,j≤100
要求:时间复杂度 O(nm)O(n**m)
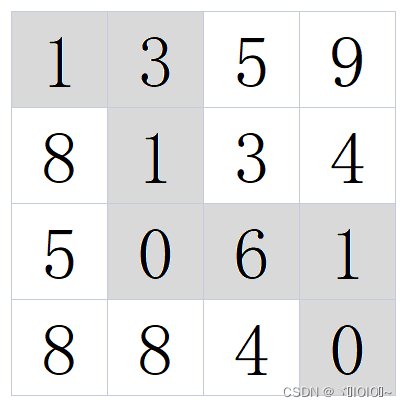
例如:当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时,对应的返回值为12,
所选择的最小累加和路径如下图所示:
示例1
输入:
[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]
返回值:
12
示例2
输入:
[[1,2,3],[1,2,3]]
返回值:
7
思路:
step 1:我们可以构造一个与矩阵同样大小的二维辅助数组,其中dp[i][j]dp[i][j]dp[i][j]表示以(i,j)(i,j)(i,j)位置为终点的最短路径和,则dp[0][0]=matrix[0][0]dp[0][0] = matrix[0][0]dp[0][0]=matrix[0][0]。
step 2:很容易知道第一行与第一列,只能分别向右或向下,没有第二种选择,因此第一行只能由其左边的累加,第一列只能由其上面的累加。
step 3:边缘状态构造好以后,遍历矩阵,补全矩阵中每个位置的dp数组值:如果当前的位置是(i,j)(i,j)(i,j),上一步要么是(i−1,j)(i-1,j)(i−1,j)往下,要么就是(i,j−1)(i,j-1)(i,j−1)往右,那么取其中较小值与当前位置的值相加就是到当前位置的最小路径和,因此状态转移公式为dp[i][j]=min(dp[i−1][j],dp[i][j−1])+matrix[i][j]dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + matrix[i][j]dp[i][j]=min(dp[i−1][j],dp[i][j−1])+matrix[i][j]。
step 4:最后移动到(n−1,m−1)(n-1,m-1)(n−1,m−1)的位置就是到右下角的最短路径和。
代码:
/**
*
* @param matrix int整型二维数组 the matrix
* @return int整型
*/
function minPathSum( matrix ) {
let n=matrix.length;
let m=matrix[0].length;
// dp[i][j]表示以当前i,j位置为终点的最短路径长
let dp=new Array(n+1);
for(let i=0;i;i++){
dp[i]=new Array(m+1)
}
// 第一列数据只能向右走,所以即为当前位置加上前一个位置
dp[0][0]=matrix[0][0];
for(let i=1;i;i++){
dp[i][0]=dp[i-1][0]+matrix[i][0];
}
// 第一行数据只能向下走,所以即为当前位置加上前一个位置
for(let j=1;j;j++){
dp[0][j]=dp[0][j-1]+matrix[0][j];
}
// 每个方块只能向下或者向右走,所以遍历到当前位置时,选择
// 上方和左方最小的数据与当前位置相加,遍历至矩阵最后一个即为答案
for(let i=1;i;i++){
for(let j=1;j;j++){
dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+matrix[i][j];
}
}
return dp[n-1][m-1];
}
module.exports = {
minPathSum : minPathSum
};
NC97 字符串出现次数的TopK问题
描述
给定一个字符串数组,再给定整数 k ,请返回出现次数前k名的字符串和对应的次数。
返回的答案应该按字符串出现频率由高到低排序。如果不同的字符串有相同出现频率,按字典序排序。
对于两个字符串,大小关系取决于两个字符串从左到右第一个不同字符的 ASCII 值的大小关系。
比如"ah1x"小于"ahb",“231”<”32“
字符仅包含数字和字母
数据范围:字符串数满足 0 \le n \le 1000000≤n≤100000,每个字符串长度 0 \le n \le 100≤n≤10,0 \le k \le 25000≤k≤2500
要求:空间复杂度 O(n)O(n),时间复杂度O(n \log k)O(nlogk)
示例1
输入:
["a","b","c","b"],2
返回值:
[["b","2"],["a","1"]]
说明:
"b"出现了2次,记["b","2"],"a"与"c"各出现1次,但是a字典序在c前面,记["a","1"],最后返回[["b","2"],["a","1"]]
示例2
输入:
["123","123","231","32"],2
返回值:
[["123","2"],["231","1"]]
说明:
"123"出现了2次,记["123","2"],"231"与"32"各出现1次,但是"231"字典序在"32"前面,记["231","1"],最后返回[["123","2"],["231","1"]]
示例3
输入:
["abcd","abcd","abcd","pwb2","abcd","pwb2","p12"],3
返回值:
[["abcd","4"],["pwb2","2"],["p12","1"]]
备注:
1 \leq N \leq 10^51≤N≤105
/**
* return topK string
* @param strings string字符串一维数组 strings
* @param k int整型 the k
* @return string字符串二维数组
*/
function topKstrings( strings , k ) {
let map=new Map();
// 先让strings数组中的字符按ASCII排序
strings.sort();
for(let i=0;i<strings.length;i++){
// 判断map中是否存在为该字符组的键
if(map.has(strings[i])){
// 如果存在则将字符去除并加1后存入map中
// let x=Number(map.get(strings[i]))+1;
let x=map.get(strings[i])+1
map.set(strings[i],x);
}else{
// 如果不存在 ,则以字符为键值为1存入map中
map.set(strings[i],1);
}
}
// 将map中的数据转换成二维数组
let arr=Array.from(map);
// 以二维中的第二列进行排序
arr.sort((a,b)=>b[1]-a[1]);
return arr.slice(0,k);
}
module.exports = {
topKstrings : topKstrings
};
NC5 二叉树根节点到叶子节点的所有路径和
描述
给定一个二叉树的根节点root,该树的节点值都在数字\ 0-9 0−9 之间,每一条从根节点到叶子节点的路径都可以用一个数字表示。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点,不能从子节点到父节点
4.总节点数目为n
例如根节点到叶子节点的一条路径是1\to 2\to 31→2→3,那么这条路径就用\ 123 123 来代替。
找出根节点到叶子节点的所有路径表示的数字之和
例如:
这颗二叉树一共有两条路径,
根节点到叶子节点的路径 1\to 21→2 用数字\ 12 12 代替
根节点到叶子节点的路径 1\to 31→3 用数字\ 13 13 代替
所以答案为\ 12+13=25 12+13=25
数据范围:节点数 0 \le n \le 1000≤n≤100,保证结果在32位整型范围内
要求:空间复杂度 O(n)O(n),时间复杂度 O(n^2)O(n2)
进阶:空间复杂度 O(n)O(n),时间复杂度 O(n)O(n)
示例1
输入:
{1,2,3}
返回值:
25
示例2
输入:
{1,0}
返回值:
10
示例3
输入:
{1,2,0,3,4}
返回值:
257
思路:
方法一(dfs):
/*
* function TreeNode(x) {
* this.val = x;
* this.left = null;
* this.right = null;
* }
*/
/**
*
* @param root TreeNode类
* @return int整型
*/
function sumNumbers( root ) {
// 方法一(dfs)
function dfs(root,pretotal){
// 当树为空时返回0
if(root==null){
return 0
}
// total为当前节点值加上上一个节点的值
let total=pretotal*10+root.val;
// 如果当前节点为跟节点则返回total
if(root.left==null&&root.right==null){
return total;
// 如果不为跟节点则深度搜素左子树加右子树
}else{
return dfs(root.left,total)+dfs(root.right,total);
}
}
return dfs(root,0);
}
module.exports = {
sumNumbers : sumNumbers
};
思路:
1、初始时,将根节点和根节点的值分别加入两个队列。每次从两个队列分别取出一个节点和一个数字,进行如下操作:
如果当前节点是叶子节点,则将该节点对应的数字加到路径之和;
如果当前节点不是叶子节点,则获得当前节点的非空子节点,并根据当前节点对应的数字和子节点的值计算子节点对应的数字,然后将子节点和子节点对应的数字分别加入两个队列。
2、搜索结束后,即可得到所有叶子节点对应的路径之和。

方法二(bfs):
// 方法二(bfs)
// 如果树为空返回0
if(root==null){
return 0;
}
// p用来存储每层的节点
let p=[];
// 结果和
let sum=0;
p.push(root);
// num用来存储每层接节点的路径和
let num=[root.val];
while(p.length!=0){
let len=p.length;
for(let i=0;i<len;i++){
let node=p.shift();
// 弹出上层路径和
let n=num.shift();
// 如果当前节点为叶节点
if(node.left==null&&node.right==null){
// 结果和加上当前的n
sum+=n;
// num.shift()
}
// 如果当前节点有左子树
if(node.left){
// 将节点推入p中
p.push(node.left);
// 将当前n乘上10在加上左节点的值
num.push(n*10+node.left.val)
}
// 同上
if(node.right){
p.push(node.right);
num.push(n*10+node.right.val)
}
}
}
return sum;
}
module.exports = {
sumNumbers : sumNumbers
};