leetcode 310 最小高度树

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：

输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。
示例 2：

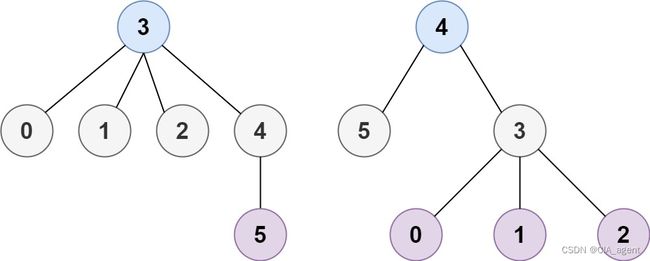
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

提示：
1 <= n <= 2 * 104
edges.length == n - 1
0 <= ai, bi < n
ai != bi
所有 (ai, bi) 互不相同
给定的输入 保证 是一棵树，并且 不会有重复的边

思路1， 先根据图的叶子节点(对应的边为1)，进行广度遍历，遍历到最后一层，则显然以最后一层为根节点的树是最小高度树

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if len(edges) == 0:
            return [0]
        degree = [set() for i in range(n)]
        visited = [0]*n
        for x in edges:
            degree[x[0]].add(x[1])
            degree[x[1]].add(x[0])
        q = collections.deque()
        for i in range(n):
            if len(degree[i]) == 1:  ## 根据题目条件，这儿不会有为 0 的
                visited[i] = 1
                q.append(i)
        ## 根据叶子节点一层一层遍历，最后一层就是结果
        while len(q) > 0:
            len_q = len(q)
            temp1, neighbor = [], set()
            for i in range(len_q):
                top = q.popleft()
                temp1.append(top)
                for x in degree[top]:
                    degree[x].remove(top)
                    if visited[x] == 0:
                        neighbor.add(x)
            if len(neighbor) == 0:
                return temp1
            for x in neighbor:
                if len(degree[x]) <= 1:  ## 为 叶子节点的入队列
                    q.append(x)
                    visited[x] = 1
        return []

思路2，以任意节点 p，利用广度优先搜索或者深度优先搜索找到以 p为起点的最长路径的终点 x；
以节点 x 出发，找到以 x为起点的最长路径的终点 y；
x 到 y 之间的路径即为图中的最长路径，找到路径的中间节点即为根节点。

import copy
class Solution:
    ## 查找 graph 里面距离 start 最远的节点
    def bfs(self, n, graph, start):
        visited  = [0]*n
        visited[start] = 1
        q = collections.deque()
        q.append(start)
        res = [start]
        while len(q) > 0:
            len_q = len(q)
            for i in range(len_q):
                top = q.popleft()
                for x in graph[top]:
                    if visited[x] == 0:
                        q.append(x)
                        res.append(x)
                        visited[x] = 1
                        graph[x].remove(top)
        return res[-1]

    ## 思路, 找出最长路径，然后找出其中的中间节点
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if len(edges) == 0:
            return [0]
        graph = [set() for i in range(n)]
        for x in edges:
            graph[x[0]].add(x[1])
            graph[x[1]].add(x[0])
        graph1 = copy.deepcopy(graph)
        ## 随机用一个点, 得到距离其最远的节点, 设为 node1,  再根据 node1 找距离 node1 最远的节点 node2
        ## node1 与 node2 是一条最长的路径
        node1 = self.bfs(n, graph1, 0)
        graph1 = copy.deepcopy(graph)
        node2 = self.bfs(n, graph1, node1)  ## node1, node2 为图中的最长路径
        father = [0]*n
        q = collections.deque([node1])
        visited = [0]*n
        visited[node1] = 1
        ## 广度遍历, 记录每个节点的 father 节点
        while len(q) > 0:
            len_q = len(q)
            for i in range(len_q):
                top = q.popleft()
                if top == node2:
                    break
                for x in graph[top]:
                    if visited[x] == 0:
                        q.append(x)
                        visited[x] = 1
                        father[x] = top
                        graph[x].remove(top)
        tmp = [node2]
        node = node2
        while node != node1:
            node = father[node]
            tmp.append(node)
        if len(tmp)%2 == 0:
            return [tmp[int((len(tmp)-1)/2)], tmp[int((len(tmp))/2)]]
        else:
            return [tmp[int(len(tmp)/2)]]