Leetcode105. 从前序与中序遍历序列构造二叉树

Leetcode105. 从前序与中序遍历序列构造二叉树

题目：
题解：
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。
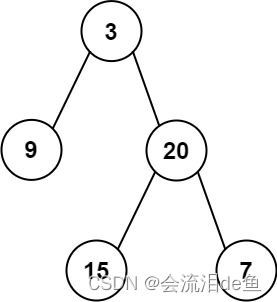
示例 1:
`

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

迭代：
我们以树

        3
       / \
      9  20
     /  /  \
    8  15   7
   / \
  5  10
 /
4

为例，它的前序遍历和中序遍历分别为
$preorder=[3,9,8,5,4,10,20,15,7]$
$inorder=[4,5,8,10,9,3,15,20,7]$
我们用一个栈 stack 来维护「当前节点的所有还没有考虑过右儿子的祖先节点」，栈顶就是当前节点。也就是说，只有在栈中的节点才可能连接一个新的右儿子。同时，我们用一个指针 index 指向中序遍历的某个位置，初始值为 0。index 对应的节点是「当前节点不断往左走达到的最终节点」，这也是符合中序遍历的，它的作用在下面的过程中会有所体现。

首先我们将根节点 3 入栈，再初始化 index 所指向的节点为 4，随后对于前序遍历中的每个节点，我们依次判断它是栈顶节点的左儿子，还是栈中某个节点的右儿子。

• 我们遍历 9。9 一定是栈顶节点 3 的左儿子。我们使用反证法，假设 9 是 3 的右儿子，那么 3 没有左儿子，index 应该恰好指向 3，但实际上为 4，因此产生了矛盾。所以我们将 9 作为 3 的左儿子，并将 9 入栈。
  • stack = [3, 9]
  • index -> inorder[0] = 4
• 我们遍历 8，5 和 4。同理可得它们都是上一个节点（栈顶节点）的左儿子，所以它们会依次入栈。
  • stack = [3, 9, 8, 5, 4]
  • index -> inorder[0] = 4
• 我们遍历 10，这时情况就不一样了。我们发现 index 恰好指向当前的栈顶节点 4，也就是说 4 没有左儿子，那么 10 必须为栈中某个节点的右儿子。那么如何找到这个节点呢？栈中的节点的顺序和它们在前序遍历中出现的顺序是一致的，而且每一个节点的右儿子都还没有被遍历过，那么这些节点的顺序和它们在中序遍历中出现的顺序一定是相反的。

这是因为栈中的任意两个相邻的节点，前者都是后者的某个祖先。并且我们知道，栈中的任意一个节点的右儿子还没有被遍历过，说明后者一定是前者左儿子的子树中的节点，那么后者就先于前者出现在中序遍历中。

因此我们可以把 index 不断向右移动，并与栈顶节点进行比较。如果 index 对应的元素恰好等于栈顶节点，那么说明我们在中序遍历中找到了栈顶节点，所以将 index 增加 1 并弹出栈顶节点，直到 index 对应的元素不等于栈顶节点。按照这样的过程，我们弹出的最后一个节点 x 就是 10 的双亲节点，这是因为 10 出现在了 x 与 x 在栈中的下一个节点的中序遍历之间，因此 10 就是 x 的右儿子。

• 回到我们的例子，我们会依次从栈顶弹出 4，5 和 8，并且将 index 向右移动了三次。我们将 10 作为最后弹出的节点 8 的右儿子，并将 10 入栈。

  • stack = [3, 9, 10]
  • index -> inorder[3] = 10

• 我们遍历 20。同理，index 恰好指向当前栈顶节点 10，那么我们会依次从栈顶弹出 10，9 和 3，并且将 index 向右移动了三次。我们将 20 作为最后弹出的节点 3 的右儿子，并将 20 入栈。

  • stack = [20]
  • index -> inorder[6] = 15

• 我们遍历 15，将 15 作为栈顶节点 20 的左儿子，并将 15 入栈。

  • stack = [20, 15]
  • index -> inorder[6] = 15

• 我们遍历 7。index 恰好指向当前栈顶节点 15，那么我们会依次从栈顶弹出 15 和 20，并且将 index 向右移动了两次。我们将
  7 作为最后弹出的节点 20 的右儿子，并将 7 入栈。

  • stack = [7]
  • index -> inorder[8] = 7

此时遍历结束，我们就构造出了正确的二叉树。

 /**
     * @param preorder
     * @param inorder
     * @return
     */
    public static TreeNode buildTree(int[] preorder, int[] inorder) {

        if (preorder == null || preorder.length == 0) return null;
        TreeNode root = new TreeNode(preorder[0]);
        Deque<TreeNode> stack = new LinkedList<>();
        stack.push(root);
        int index = 0;
        for (int i = 1; i < preorder.length; i++) {
            int preorderVal = preorder[i];
            TreeNode node = stack.peek();
            if (node.value != inorder[index]) {
                node.left = new TreeNode(preorderVal);
                stack.push(node.left);
            } else {
                while (!stack.isEmpty() && stack.peek().value == inorder[index]) {
                    node = stack.pop();
                    index++;
                }
                node.right = new TreeNode(preorderVal);
                stack.push(node.right);
            }
        }
        return root;
    }