CSP-S 2022 游记&题解
赛前七日
赛前一个星期住在苏州,10.29 比赛前的星期天还打了 CF 的 Div1。 第一次场切了 Div1.前四道。当时觉得这好像不是状态不错的现象,这可能是要把运气透支的预兆…然后一个星期后的 CSP 就寄了
今年高一了,说起来还是首次参加 CSP-S。初一初二两年因为水平不够没有报 S。上初三之后报了,但是被苏州地狱难度的初赛卡在了起跑线上。
算是憋了一年的气,2022年 CSP-S 终于稳稳当当进了第二轮,虽然说赛前一段时间比较佛系,但是心里对分数的期望还是比较高的。自我期望想有 300 来着。
赛前一个星期每天在和 LZJ 大牛在学校机房一起做题,挺久没回学校的了,每天中午和晚饭后还会去找同学踢球。和同学走在食堂的路上谈天说地的时候,仿佛找到了一点停课前快乐的校园生活的感觉。但是星期日很快到来,一眨眼就站在了考场的门前。
校园春雨池一景
踏上赛场
那天太阳挺大,下午两点苏州无锡的各路大仙都来到学校三元楼门口准备吊打我。
进考场的时候还发生了点小插曲。因为苏高中机房地板里不知道有什么金属,监考老师拿安检棒扫我鞋的时候一直在叫,我当时心里一直 mmp,总不能叫我在机房拖鞋吧。后来监考老师让我站在外面扫了一次,没有问题才安心坐下来。
T1
发题之后,按顺序先看了一眼 T1 ,当时没有看到每个点只能走一次的限制,想到了一个贪心的假做法,心里还想着 CSP t1怎么会这么水,然后准备开始写代码的时候发现了不太对劲,回头看了题面发现少读了一条限制。就这样浪费了比赛开始时的 15 min。
不过好在枚举中间两个点的技巧,前段时间在打叉姐出的模拟赛时用到过,所以没多久就想到了。
口胡一下。就是首先 bfs 求出每两个点之间的最短路。然后对每个点 u u u 储存一个列表 v [ u ] v[u] v[u],里面存所有与 u u u 和 起点 0 0 0 距离均不大于 k k k 的点。然后对每一个列表,将所有点按照权值降序排序。
路径上的 4 4 4 个 点 a , b , c , d a,b,c,d a,b,c,d 中,去枚举中间两个点 b , c b,c b,c,然后一定是 a ∈ v [ b ] , d ∈ v [ c ] , a ≠ b , a ≠ c , d ≠ b a\in v[b],d\in v[c],a\neq b,a\ne c,d\ne b a∈v[b],d∈v[c],a=b,a=c,d=b。那么因为列表中元素已经按照权值降序排序了,只要维护两个列表中当前最优的合法位置,相同就考虑后移其中一个,不相同就直接取答案。这个过程是 O ( 1 ) \operatorname O(1) O(1) 的。
- 时间复杂度: O ( n 2 ) \operatorname O(n^2) O(n2)
- 空间复杂度: O ( n 2 ) \operatorname O(n^2) O(n2)
一道技巧性的图论模拟题。前前后后大概花了 45 min 时间,细细回想浪费 15 min 确实不应该。
现场 code:
#include T2
然后开始看 t2。一道博弈,很自然想到对两数的正负性进行讨论。
当 A 决策确定,B 的决策是比较好考虑的:
- 当 A 取正数,B 一定会取 min \min min
- 当 A 取 0 0 0 ,B 取什么都一样
- 当 A 取负数,B 一定会取 max \max max
然后考虑 A 的决策。
- 如果区间内有正数可选,考虑取正数的最优答案,需要讨论 B 取的 m i n b min_b minb 的正负性
- m i n b > 0 min_b>0 minb>0,A 取最大正数
- m i n b = 0 min_b=0 minb=0,A取什么都一样
- m i n b < 0 min_b<0 minb<0,A取最小正数
- 如果区间内有 0 0 0 可选,那么最优答案至少为 0 0 0
- 如果区间内有负数可选,考虑取负数的最优答案,需要讨论 B 取的 m a x b max_b maxb 的正负性
- m a x b > 0 max_b>0 maxb>0,A 取最大负数
- m a x b = 0 max_b=0 maxb=0,A 取什么都一样
- m a x b < 0 max_b<0 maxb<0,A 取最小负数。
讨论到这里这题就做完了,只需要对每个询问,求出 A区间最大最小正数、A区间最大最小负数、A区间是否有 0 0 0、B 区间最大最小值,就可以模拟这个讨论过程求出最大答案。维护区间最值的方式显然可以选择 ST 表。最大正数和最小负数都好维护;对于最小正数和最大负数,只要再开一个 ST 表,储存所有 正 数 − I N F 正数-INF 正数−INF 和 负 数 + I N F 负数+INF 负数+INF 即可。全过程前后用到 6 个 ST 表。
- 时间复杂度: O ( n log n + q ) \operatorname O(n\log n+q) O(nlogn+q)
- 空间复杂度: O ( n log n ) \operatorname O(n\log n) O(nlogn)
这道题感觉思维上比较有意思,如果逻辑清楚的话做起来会很轻松,赛事很顺利,开始 1h 多一点的时候完成了t2.
赛事 code:
#include T3
这道诈骗题可以说是我考的稀烂的罪魁祸首。
比赛的时候想到了这样一个结论:答案为 YES 的充要条件是所有点出度为1(形成了一个内向基环树森林)。
然后在剩下的两个多小时的时间内,我的状态就 be like:
这怎么搞?趴下来想一下。想不出来了,玩一会水笔。画个图吧?好像没啥用…
当时的思维卡在了什么地方?大概就是摧毁修复一个点的所有入边,因为一个点的所有入边对应点是离散的,没有想到很好的数据结构能一次性地同时修改这些点地出度。
然后,就没有然后了,坐牢了很久。T4 看了一下,感觉 T3 更好做就继续钻研 T3。毕竟当时还想着目标 300+,心里就是想把这题攻克了。眼看时间不够了,就写了一个把边逐个修改的暴力。
出考场之后,在门口看见 无锡队长 三维,问了他的战况。他很假的在那里说自己不会 t4,没有 AK。
然后我就问他 t3 咋做。
他说:”哈希。“
哈希…,哈希…,对啊,哈希,卧槽!
一听到这两个字我就拨云见日,茅塞顿开。之前学过 Sum Hashing 的技巧,但是赛场上我又没能把这道图论题和八竿子打不着的哈希联系起来。玉玉了
大概口胡一下:
可以发现图合法的条件是,当前图的每一个连通块都是一个内向基环树。进一步思考发现,充要条件就是所有点的出度都为 1 1 1。
那么我们想办法同时维护和操作每个点的出度值。用 Sum Hashing解决。
对于出度数组 out[],我们给它选定一个哈希系数 p p p 和一个模数 M O D MOD MOD,来把它表示成一个哈希量 ∑ o u t [ i ] × p i % M O D \sum out[i]\times p^i\%MOD ∑out[i]×pi%MOD。节点 i i i 对应的哈希量就是 o u t [ i ] × p i out[i]\times p^i out[i]×pi。
同时维护对于每个点 u u u,其所有入边节点的哈希量之和 s u m u = ∑ ( u , v ) ∈ E 1 × p v % M O D sum_u=\sum\limits_{(u,v)\in E} 1\times p^v \%MOD sumu=(u,v)∈E∑1×pv%MOD,以及当前没有损坏的入边节点的哈希量之和 c u r [ u ] = ∑ ( u , v ) ∈ E , 且 ( u , v ) 没 有 损 坏 1 × p v cur[u]=\sum\limits_{(u,v)\in E,且(u,v)没有损坏} 1\times p^v%MOD cur[u]=(u,v)∈E,且(u,v)没有损坏∑1×pv。
对于操作 1 , h ← h − p x , c u r y ← c u r y − p x h\gets h-p^x,cur_y\gets cur_y-p^x h←h−px,cury←cury−px
对于操作 2, h ← h − c u r y , c u r y ← 0 h\gets h-cur_y,cur_y\gets0 h←h−cury,cury←0
对于操作 3, h ← h + p x , c u r y ← c u r y + p x h\gets h+p^x,cur_y\gets cur_y+p^x h←h+px,cury←cury+px
对于操作 4, h ← h + s u m y − c u r y , c u r y ← s u m y h\gets h+sum_y-cur_y,cur_y\gets sum_y h←h+sumy−cury,cury←sumy
如果当前时刻下,满足 h = Σ 1 × p i h=Σ1\times p^i%MOD h=Σ1×pi,说明所有点出度都为 1 1 1。那么就视为合法。
为了防止哈希冲突,用两个不同模数做两遍,两遍都合法的时刻才被视为合法。
- 时间复杂度: O ( n + m + q ) \operatorname O(n+m+q) O(n+m+q)
- 空间复杂度: O ( n + m + q ) \operatorname O(n+m+q) O(n+m+q)
赛后补的 code:
#include T4
说实话这题考场上没有认真去想,把后半段时间全部花在了 T3 上。这实在是重大失误。当时临结束时连最最简单的链上暴力都没来得及打,只交了三个程序。现在想来,如果当时花时间写个 40 分左右的暴力,那么分数也早该上 300 了。
赛后出来的时候,gzy,lyx,sw 他们都在群里讨论 t4,可是我连暴力都没打,心态有点崩。当时他们讨论的做法,说是 “ddp”。To be Honest,我在此之前确实是没听过这个算法,感觉很玄妙的样子。后来查了一下,原来是 ”动态dp“ 的意思。这个我倒是有所耳闻过,但是没有写过相关的题目,所以就没能在现场读题时看出来这个做法。
唉,还是败在了经验和积累上。
后来重新学习了一遍动态 dp 算法。这是一个用来解决树上 dp+查询 问题的常用模型。像 t4 这道 书上路径 dp+询问的模型,如果做过类似的题的话应该很快会想到(可惜我没做过)。
首先,如果问题在一条链上,那么就自然而然想到了 dp 方式:
-
设 f i , j f_{i,j} fi,j 表示考虑到第 i i i 个节点,上一个选定的中转节点与 i i i 距离为 j j j 的最小代价。
-
转移式: { f i , 0 = min f i − 1 , j + a i f i , j = f i − 1 , j − 1 \begin{cases}f_{i,0}=\min{f_{i-1,j}}+a_i\\f_{i,j}=f_{i-1,j-1}\end{cases} {fi,0=minfi−1,j+aifi,j=fi−1,j−1
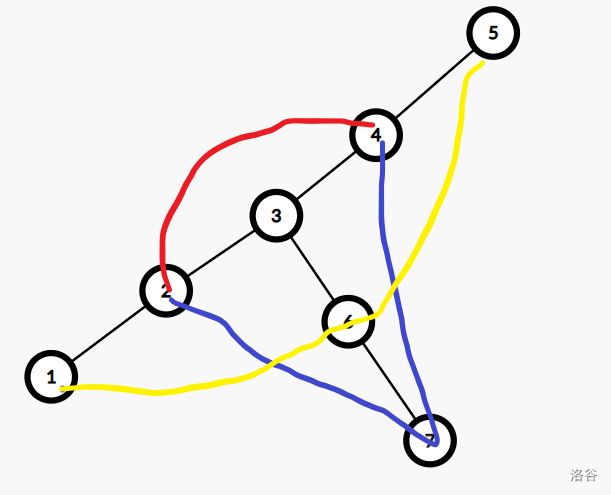
想一想就发现,当 k ≤ 2 k\le 2 k≤2 时,我们的确只需要考虑 x → y x\to y x→y 路径上的点,因为如果要走到某个节点的分枝上(如下图,蓝色路径不如红色路径优),一定不会更优。
只有当 k = 3 k=3 k=3 时,才可能考虑到路径上节点的分枝,但是可以发现,只会考虑到与路径上节点直接相连的节点(如下图,蓝色路径不如红色路径优,只需要考虑黄色路径这种)。
结合这个情况,我们发现原先的 dp 状态依然可行,我们只需要添加一种转移,考虑走到当前第 i i i 个节点的某个相邻节点上就行。且所有相邻节点在距离上等价,我们只需要选相邻节点中权值最小的即可。于是我们记 a i a_i ai 为 i i i 点的权值, b i b_i bi 为与 i i i 相邻的点中最小的权值。有以下转移式:
{ f i , 0 = min f i − 1 , 0 / 1 / 2 + a i f i , 1 = min ( f i − 1 , 0 , min f i − 1 , 1 + b i ) f i , 2 = f i − 1 , 1 \begin{cases} f_{i,0}=\min{f_{i-1,0/1/2}}+a_i\\ f_{i,1}=\min(f_{i-1,0},\min{f_{i-1,1}+b_i})\\ f_{i,2}=f_{i-1,1} \end{cases} ⎩⎪⎨⎪⎧fi,0=minfi−1,0/1/2+aifi,1=min(fi−1,0,minfi−1,1+bi)fi,2=fi−1,1
到了这里,我们就可以每次询问把整个路径取出来,然后在链上 dp 求出答案。这就是一个 O ( q n ) \operatorname O (qn) O(qn) 的算法了。
接下来考虑如何优化每次询问的过程。由于 dp 的第二维状态很小,只有 3,且先 + + + 后取 min \min min 的运算满足结合律,所以我们考虑用新定义的矩阵乘法去进行转移。
我们定义,对于矩阵 A , B A,B A,B:
C = A ∗ B ↔ C i , j = min l { A i , l + B l , j } C=A*B\\ \leftrightarrow\\ C_{i,j}=\min_l\{A_{i,l}+B_{l,j}\} C=A∗B↔Ci,j=lmin{Ai,l+Bl,j}
然后考虑 k = 3 k=3 k=3 时,如何用矩阵从 f i − 1 , 0 / 1 / 2 f_{i-1,0/1/2} fi−1,0/1/2 转移到 f i , 0 / 1 / 2 f_{i,0/1/2} fi,0/1/2 ,根据上面推出的转移式:
( f i , 0 f i , 1 f i , 2 ) = ( a i a i a i 0 b i ∞ ∞ 0 ∞ ) ∗ ( f i − 1 , 0 f i − 1 , 1 f i − 1 , 2 ) \begin{pmatrix}f_{i,0}\\f_{i,1}\\f_{i,2}\end{pmatrix}= \begin{pmatrix}a_i&a_i&a_i\\0&b_i&\infty\\\infty&0&\infty\end{pmatrix}* \begin{pmatrix}f_{i-1,0}\\f_{i-1,1}\\f_{i-1,2}\end{pmatrix} ⎝⎛fi,0fi,1fi,2⎠⎞=⎝⎛ai0∞aibi0ai∞∞⎠⎞∗⎝⎛fi−1,0fi−1,1fi−1,2⎠⎞
同样根据转移式,对于 k = 2 k=2 k=2:
( f i , 0 f i , 1 ∞ ) = ( a i a i ∞ 0 ∞ ∞ ∞ ∞ ∞ ) ∗ ( f i − 1 , 0 f i − 1 , 1 ∞ ) \begin{pmatrix}f_{i,0}\\f_{i,1}\\\infty\end{pmatrix}= \begin{pmatrix}a_i&a_i&\infty\\0&\infty&\infty\\\infty&\infty&\infty\end{pmatrix}* \begin{pmatrix}f_{i-1,0}\\f_{i-1,1}\\\infty\end{pmatrix} ⎝⎛fi,0fi,1∞⎠⎞=⎝⎛ai0∞ai∞∞∞∞∞⎠⎞∗⎝⎛fi−1,0fi−1,1∞⎠⎞
对于 k = 1 k=1 k=1:
( f i , 0 ∞ ∞ ) = ( a i ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ) ∗ ( f i − 1 , 0 ∞ ∞ ) \begin{pmatrix}f_{i,0}\\\infty\\\infty\end{pmatrix}= \begin{pmatrix}a_i&\infty&\infty\\\infty&\infty&\infty\\\infty&\infty&\infty\end{pmatrix}* \begin{pmatrix}f_{i-1,0}\\\infty\\\infty\end{pmatrix} ⎝⎛fi,0∞∞⎠⎞=⎝⎛ai∞∞∞∞∞∞∞∞⎠⎞∗⎝⎛fi−1,0∞∞⎠⎞
(这里为了方便,一律把矩阵视为 3 × 3 3\times 3 3×3 了)
那么对于每个点 u u u,都有其对应矩阵。对于一个询问 x → y x\to y x→y 我们可以通过类似倍增求 LCA 的方式将 x , y x,y x,y 向上每次跳 2 i 2^i 2i 的长度,跳后乘上经过的路径上的矩阵乘积。那么只要先倍增预处理 m t u , i mt_{u,i} mtu,i 表示点 u u u 向上 2 i 2^i 2i 路径上的矩阵之和。
tips:因为矩阵乘法不满足交换律,所以我们对每个倍增值,都要维护正反两种顺序的乘积。
跳 LCA 的过程不多赘述,维护 x , y x,y x,y 分别有两个矩阵。左矩阵不断右乘,右矩阵不断左乘。总之跳完以后我们将左矩阵和右矩阵在 LCA 处合并,得到一个总的转移矩阵 M M M。
我们将开始的矩阵视为 ( ∞ ∞ 0 ) \begin{pmatrix}\infty\\\infty\\0\end{pmatrix} ⎝⎛∞∞0⎠⎞ ,那么答案为 M 0 , 2 M_{0,2} M0,2。(当 k < 2 k<2 k<2 时为 M 0 , k − 1 M_{0,k-1} M0,k−1)
这样一次询问的过程是 O ( log n ) \operatorname O(\log n) O(logn) 的。
- 时间复杂度: O ( k 3 ( n + q ) log n ) \operatorname O(k^3(n+q)\log n) O(k3(n+q)logn)
- 空间复杂度: O ( k 2 n log n + q ) O(k^2n\log n+q) O(k2nlogn+q)
放一下赛后补的 code:
#include 沪宁线上
考完试坐汽车回家,在高速上看着窗外飞速闪过的霓虹灯和车辆,想起自己发挥的这么差,不禁玉玉了起来.
回到家 emo 了很久。总结了以下几个发挥失常的原因。
- 比赛经验不足,对时间的规划不恰当,没有很好的利用时间。
- t1读题错误,轻敌了导致浪费了一些时间,搞乱了心态。
- t3和t4,都是一些比较管用的处理技巧,现场没有想到。这是经验问题,以后还需多加练习和总结。
- 低估了暴力分的重要性,如果赛场上求稳,放弃t3,t4的正解,分别打好一些暴力,两题的暴力分加起来能有100+,那么300+也就稳了。可见赛场上想不出来的题死磕未必是正确策略。
出分日
洛谷和 INFOJ 上的估分,区间大概是[205,215] 。原因是 t3 的暴力被卡了,里面甚至还有写挂的小漏洞。只能拿不超过 15 分,t1t2 稳过了。心里还是没什么底,这个分数虽说一等是没有太大问题了,但是距离 7 级可能还有差距,并且到不了给自己定的省 rk50 以内的目标了。
11 月 7 日的傍晚,CCF又推迟了出榜时间。在水洛谷评论区的时候,看见有 HN 的选手说看到分了,T3 数据很水,全 NO 都有 45。当时心中还没有什么波澜,没过多久出分了。我上网站一看,还真是走了狗屎运,T3 的暴力程序时间和写挂的漏洞处都没有被卡很多,甚至拿了整整 60 分。。总分 260,11.17日时名单公示,一等有了,7级也有了,只是省 rk 50没达到,只有rk72。
还是有点难过,从年初开始停课,至今已有10个月之久。在这期间查漏补缺,学习了大量之前不熟悉的数据结构、算法和做题技巧。c f从青名的菜鸡,也一步步打上 master,虽说不是很高,但是我感觉自己的进步速度是相当快的。在9~10月 的 hb 模拟中,我基本也是发挥不错的。
这次 CSP 的发挥失常给了我当头一棒。如果换做一年前的我来做,想必也有 200+,260也不是什么难事。如果单看分数,我可能这一年是毫无长进。心里还是扒了一扒,如果后两题求稳写暴力并且没挂,320 还是有的,如果结合做题经验想出了其中一个正解,那么 360 也是有的。可是赛后再谈这些已经是白日做梦。我只能当这次运气不好,未来的某一天还会给我还运的吧。☹
本文写于11.17,也就是出榜之后。距离 NOIP 2022还有不到 10 天。希望这 10 天里自己能收起其他杂念,专心备战。祝大家 NOIP 2022 rp++。