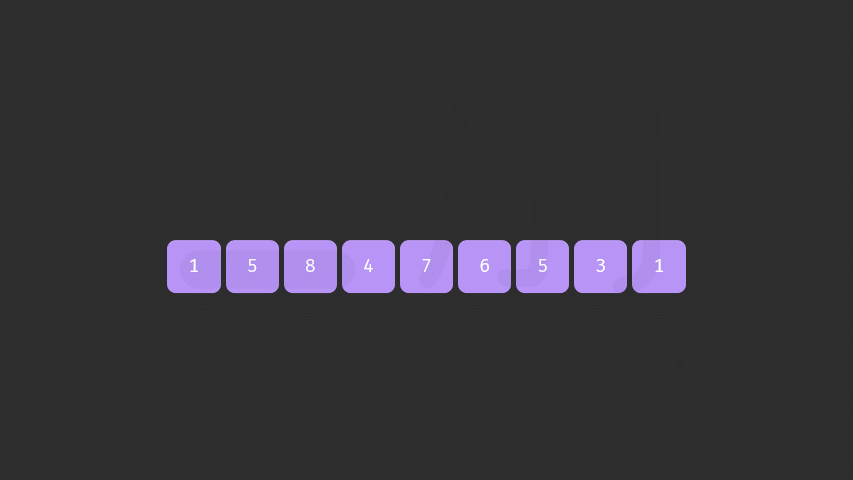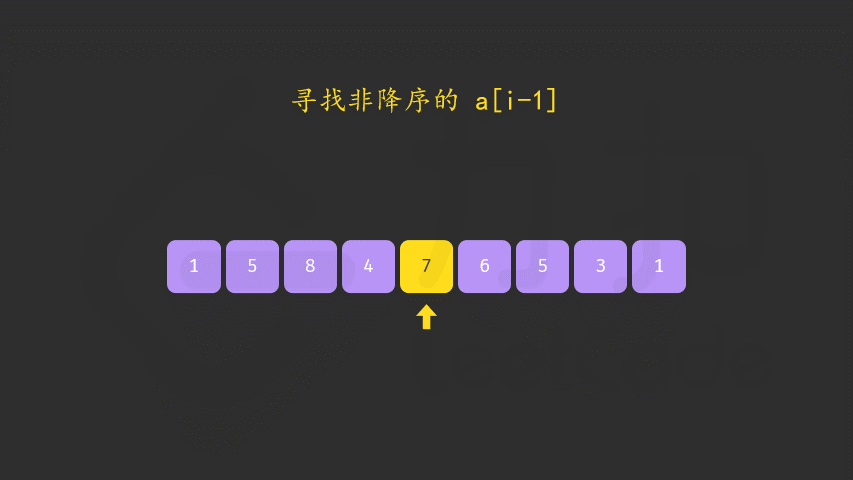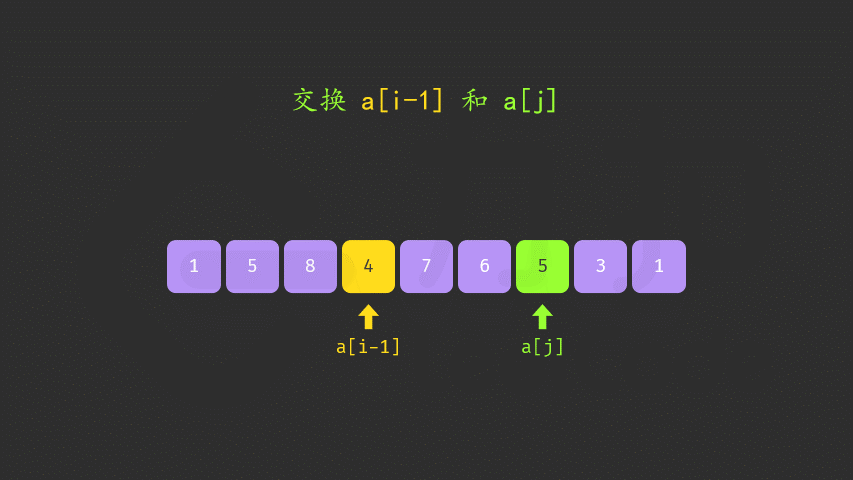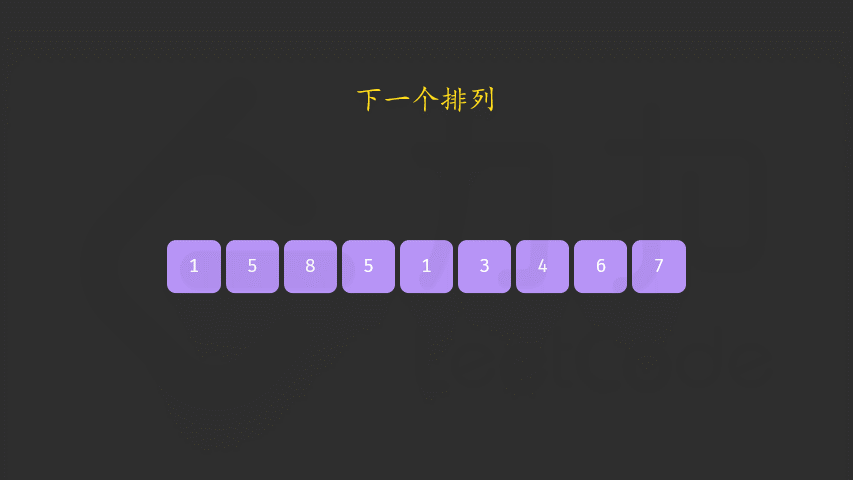力扣刷题笔记

写在前面

该怎么刷题？

个人认为首先需要掌握数据结构、基础算法，然后再去练习。掌握思路，再写代码。笔者其他文章有数据结构及算法。

刷题的方法

   进制转化

十进制转化为8位的二进制，前面不足补0 

    public static String toBinary(String num) {
        //int(十进制)转化为二进制字符
        String numBinary = Integer.toBinaryString(Integer.valueOf(num));
        while (numBinary.length() < 8) {
            numBinary = "0" + numBinary;
        }
        return numBinary;
    }

    //转化为8位的二进制，前面不足补0 

二进制数转换为十进制数

1)使用Integer类的Integer.parseInt()方法。

2)自己编写转换逻辑。

方法1：使用Integer.parseInt()实现二进制转换为十进制

import java.util.Scanner;

class BinaryToDecimal {

    public static void main(String args[]){

       Scanner input = new Scanner( System.in );

       System.out.print("Enter a binary number: ");

       String binaryString =input.nextLine();
       
 //数字代表进制，前面字符表示该进制字符串
       System.out.println("Output: "+Integer.parseInt(binaryString,2));

    }

}

数组

力扣15

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

468. 验证IP地址

HJ18 识别有效的IP地址和掩码并进行分类统计

HJ107 求解立方根

最大公约数

1. 暴力法
2. 辗转相除法
3. 更相减损法
4. 辗转+更相

public class Main{

    public static void main(String[] args){
        int a = 35;
        int b = 21;
        System.out.println(getGreatestCommonDivisor(a, b));
        System.out.println(subtract(a, b));
        System.out.println(subtractV2(a, b));
    }

    private static int getGreatestCommonDivisor(int a, int b) {
        int result;
        if (a > b) {
            result = divide(a, b);
        } else {
            result = divide(b, a);
        }
        return result;
    }

    private static int divide(int a, int b) {
        if (a % b == 0) {
            return b;
        } else {
            //辗转相除法：两个正整数a和b（a>b），它们的最大公约数等于 a除以b的余数c 和 b 之间的最大公约数
            //以此类推，逐渐把两个较大整数之间的运算简化成两个较小整数之间的运算，直到两个数可以整除，或者其中一个数减小到1为止
            //缺点：当两个整数较大时，a%b性能较低
            return divide(b, a % b);
        }
    }

    private static int subtract(int a, int b) {
        if (a == b) {
            return a;
        } else if (a > b) {
            //更相减损法：两个正整数a和b（a>b），它们的最大公约数等于 a-b的差值c 和 较小数b 的最大公约数
            //以此类推，逐渐把两个较大整数之间的运算简化成两个较小整数之间的运算，直到两个数可以相等为止，最大公约数就是最终相等的两个数
            //缺点：不稳定的算法，当两数相差悬殊时，比如计算10000和1，就要递归9999次
            return subtract(a - b, b);
        } else {
            return subtract(b - a, a);
        }
    }

    private static int subtractV2(int a, int b) {
        if (a == b) {
            return a;
        }
        //保证a > b
        if (a < b) {
            return subtractV2(b, a);
        }
        //位与运算判断奇偶
        if ((a & 1) == 0 && (b & 1) == 0) {
            //当a和b均为偶数，gcd(a,b) = 2*gcd(a/2, b/2) = 2*gcd(a>>1, b>>1)
            return subtractV2(a >> 1, b >> 1) << 1;
        } else if ((a & 1) == 0) {
            //当a为偶数，b为奇数，gcd(a,b) = gcd(a/2, b) = gcd(a>>1, b)
            return subtractV2(a >> 1, b);
        } else if ((b & 1) == 0) {
            //当a为奇数，b为偶数，gcd(a,b) = gcd(a, b/2) = gcd(a, b>>1)
            return subtractV2(b >> 1, a);
        } else {
            //当a和b均为奇数，利用更相减损法运算一次，gcd(a,b) = gcb(a - b, b)，此时a-b必然是偶数，又可以继续进行移位运算。
            return subtractV2(a - b, b);
        }
    }

}

如何判断一个数是否为2的整数次幂

1. 暴力法
2. 移位法
3. 二进制

先把2的正整数次幂转换成二进制数，如下表

十进制	二进制	是否为2的整数次幂
8	1000B	是
16	10000B	是
32	100000B	是
64	1000000B	是
100	1100100B	否

接下来如果把这些2的整数次幂各自减1

十进制	二进制	原数值-1	是否为2的整数次幂
8	1000B	111B	是
16	10000B	1111B	是
32	100000B	11111B	是
64	1000000B	111111B	是
100	1100100B	1100011B	否

这时如果将原数值和它减1的结果进行按位与计算，也就是n&(n-1)

十进制	二进制	原数值-1	n&n-1	是否为2的整数次幂
8	1000B	111B	0	是
16	10000B	1111B	0	是
32	100000B	11111B	0	是
64	1000000B	111111B	0	是
100	1100100B	1100011B	1	否

所以对于一个整数n，只需要计算n&(n-1)的结果是不是0就可以判断了。
时间复杂度为O(1)。

int isPowerOf2V3(int num) {
	return (num & num-1) == 0;
}

下一个排列

字典序算法

方法一：两遍扫描

字符串

力扣22

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

输入：n = 1
输出：["()"]

方法一：深度优先遍历

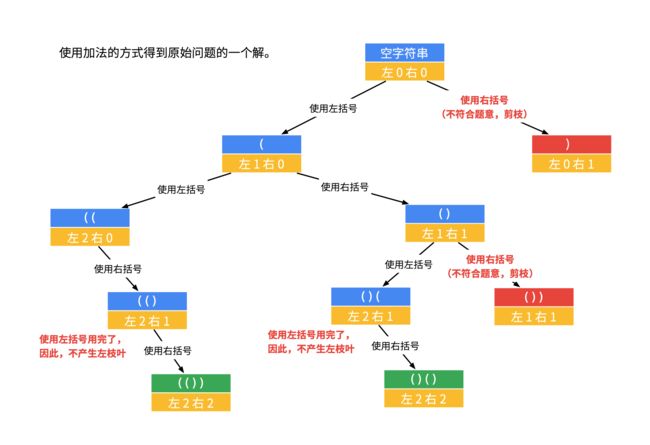
我们以 n = 2 为例，画树形结构图。方法是 「做减法」。

1. 当前左右括号都有大于 00 个可以使用的时候，才产生分支；
2. 产生左分支的时候，只看当前是否还有左括号可以使用；
3. 产生右分支的时候，还受到左分支的限制，右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候，才可以产生分支；
4. 在左边和右边剩余的括号数都等于 00 的时候结算。

方法二：广度优先遍历

广度优先遍历，得程序员自己编写结点类，显示使用队列这个数据结构。深度优先遍历的时候，就可以直接使用系统栈，在递归方法执行完成的时候，系统栈顶就把我们所需要的状态信息直接弹出，而无须编写结点类和显示使用栈。

广度优先遍历；
自己使用栈编写深度优先遍历；
使用系统栈的深度优先遍历（回溯算法）。

方法三：暴力法

我们可以生成所有 2^2n  个 `(' 和`)’ 字符构成的序列，然后我们检查每一个是否有效即可。

方法四：动态规划

什么是动态规划？在此题中，动态规划的思想类似于数学归纳法，当知道所有 i 本题最核心的思想是，考虑 i=n 时相比 n-1 组括号增加的那一组括号的位置。

思路：
当我们清楚所有 i 它一定是一个左括号，那么它可以和它对应的右括号组成一组完整的括号 "( )"，我们认为这一组是相比 n-1 增加进来的括号。

那么，剩下 n-1 组括号有可能在哪呢？

【这里是重点，请着重理解】

剩下的括号要么在这一组新增的括号内部，要么在这一组新增括号的外部（右侧）。

既然知道了 i

"(" + 【i=p时所有括号的排列组合】 + ")" + 【i=q时所有括号的排列组合】

其中 p + q = n-1，且 p q 均为非负整数。

事实上，当上述 p 从 0 取到 n-1，q 从 n-1 取到 0 后，所有情况就遍历完了。

注：上述遍历是没有重复情况出现的，即当 (p1,q1)≠(p2,q2) 时，按上述方式取的括号组合一定不同。

二叉树

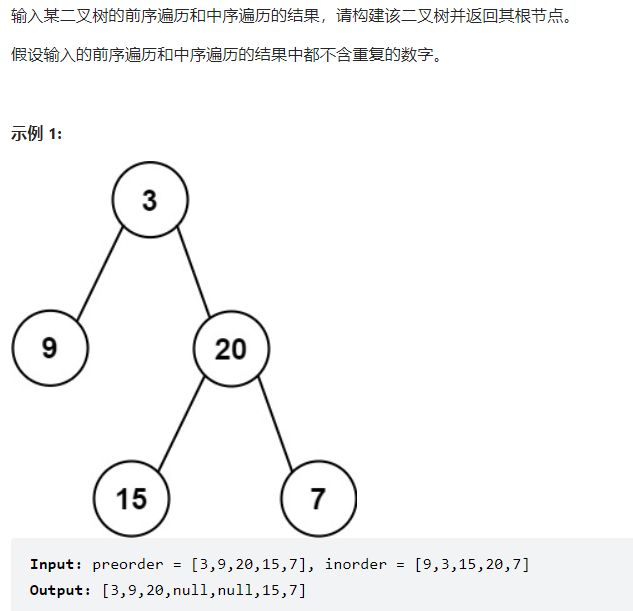
剑指 Offer 07. 重建二叉树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    HashMap map = new HashMap<>();//标记中序遍历
    int[] preorder;//保留的先序遍历，方便递归时依据索引查看先序遍历的值

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        //将中序遍历的值及索引放在map中，方便递归时获取左子树与右子树的数量及其根的索引
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        //三个索引分别为
        //当前根的的索引
        //递归树的左边界，即数组左边界
        //递归树的右边界，即数组右边界
        return recur(0,0,inorder.length-1);
    }

    TreeNode recur(int pre_root, int in_left, int in_right){
        if(in_left > in_right) return null;// 相等的话就是自己
        TreeNode root = new TreeNode(preorder[pre_root]);//获取root节点
        int idx = map.get(preorder[pre_root]);//获取在中序遍历中根节点所在索引，以方便获取左子树的数量
        //左子树的根的索引为先序中的根节点+1 
        //递归左子树的左边界为原来的中序in_left
        //递归左子树的右边界为中序中的根节点索引-1
        root.left = recur(pre_root+1, in_left, idx-1);
        //右子树的根的索引为先序中的 当前根位置 + 左子树的数量 + 1
        //递归右子树的左边界为中序中当前根节点+1
        //递归右子树的右边界为中序中原来右子树的边界
        root.right = recur(pre_root + (idx - in_left) + 1, idx+1, in_right);
        return root;

    }

}

栈

155. 最小栈

 解法一：

辅助栈

解法二：

元组解法