LeetCode_栈专题

一.接雨水

42.题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

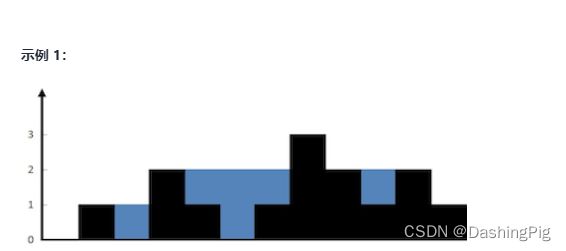
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/trapping-rain-water
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

答案：全局和局部思想+栈+碗的左中右组成思想
我：仅仅把碗看成由左右组成，不灵活地迁移关于栈的括号例子

使用数据结构如下：
需要一个栈，存放碗左中的坐标
需要一个res，计算答案

处理规则如下：
求一个全局大碗，大碗里有许多小碗，能处理就立刻处理，很像四则运算
栈里存放左中的坐标，必须左高>=中高！！！
当前遍历的i为右，处理完此碗，i被看成是左或中入栈
当右高>中高，可以处理此碗（栈里必须至少含有左中两个元素！！！）
处理的雨水面积公式：宽=右坐标-左坐标-1； 高=min(左高，右高)-中高

细节如下：
1.当（栈空 || height[i]<=height[top]）,入栈，break；
2.当height[i]>height[top],
（1）当栈元素>=2,处理雨水，top出栈，回到12判断，循环；
（2）当栈元素<2,top出栈，回到12判断，循环；

反思：
一开始我想到用栈，迁移了括号处理的方法后，把碗看成由左右边缘构成，并使用局部处理+能处理就快处理的原则，大碗是由小碗构成的嘛，没有思路的时候，往往将问题拆解，为了求全局问题，只要处理好局部问题就好了，然而想了很久都没想出来，于是去看官方答案，发现只需要把碗看成由左中右构成！我漏了一个中。
所以，迁移知识要灵活，什么情况用什么样的变形方案。

代码

//答案：全局和局部思想+栈+碗的左中右组成思想
//我：仅仅把碗看成由左右组成，不灵活地迁移关于栈的括号例子

//使用数据结构如下：
//需要一个栈，存放碗左中的坐标
//需要一个res，计算答案

//处理规则如下：
//栈里存放左中的坐标，必须左高>=中高！！！
//当前遍历的i为右，处理完此碗，i被看成是左或中入栈
//当右高>中高，可以处理此碗（栈里必须至少含有左中两个元素！！！）
//处理的雨水面积公式：宽=右坐标-左坐标-1； 高=min(左高，右高)-中高

//细节如下：
//1.当（栈空 || height[i]<=height[top]）,入栈，break；
//2.当height[i]>height[top],
//  （1）当栈元素>=2,处理雨水，top出栈，回到12判断，循环；
//  （2）当栈元素<2,top出栈，回到12判断，循环；
class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> st;//生成一个存放左中坐标的栈
        int res = 0;

        for(int i = 0; i <= height.size()-1; ++i)
        {
            while(1)
            {
                if(st.empty() || height[i]<=height[st.top()])//当栈空或者右高<=中或左高，入栈
                {
                    st.push(i);
                    break;
                }
                else if(height[i]>height[st.top()])//当右高>中或左高，可能处理雨水
                {
                    if(st.size()>=2)//当栈中含有左中，处理雨水
                    {
                        int tmp = st.top();//tmp存放中坐标
                        st.pop();//出栈
                        res += (i-st.top()-1)*(min(height[i], height[st.top()])-height[tmp]);
                    }
                    else//当栈中不含左中，出栈
                        st.pop();//出栈
                }
            }
        }
        return res;
    }
};

二.简化路径

71.题目

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 ‘/’ 开头），请你将其转化为更加简洁的规范路径。

在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点 （…） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠（即，’//’）都被视为单个斜杠 ‘/’ 。 对于此问题，任何其他格式的点（例如，’…’）均被视为文件/目录名称。

请注意，返回的 规范路径 必须遵循下述格式：

始终以斜杠 ‘/’ 开头。
两个目录名之间必须只有一个斜杠 ‘/’ 。
最后一个目录名（如果存在）不能 以 ‘/’ 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 ‘.’ 或 ‘…’）。
返回简化后得到的 规范路径 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/simplify-path
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

数据结构如下：
使用2个栈，stRes存放反结果，stTmp作获取结果的中转站
使用字符串str，存放当前字符串,每次用完清空

规则如下：
当遇到/或i为终坐标, 处理完后str清空,处理如下
当遇到.或str空，不处理
2.当遇到…且栈不空，则出栈
3.当遇到不是.且不是… ，则 当前串 入栈
当最后且栈空, 则返回/

反思：
当需要用到上一个历史记录的时候，一般需要使用栈；
如，迷宫求解问题；

代码

//数据结构如下：
//使用2个栈，stRes存放反结果，stTmp作获取结果的中转站
//使用字符串str，存放当前字符串,每次用完清空

//规则如下：
//当遇到/或i为终坐标, 处理完后str清空,处理如下
//当遇到.或str空，不处理
//2.当遇到..且栈不空，则出栈
//3.当遇到不是.且不是.. ，则 当前串 入栈
//当最后且栈空, 则返回/
class Solution {
public:
    string simplifyPath(string path) {
        stack<string> stRes, stTmp;
        string str;

        for(int i = 0; i <= path.length()-1; ++i)
        {
            if(path[i] == '/' || i == path.length()-1)//遇到/或i为终坐标，则处理,然后清空str
            {
                if(i == path.length()-1 && path[i] != '/')//special state
                    str += path[i];

                int tmp = judgeC(str);//获取条件
                if(tmp == 2 && !stRes.empty())
                {
                    stRes.pop();
                }
                else if(tmp == 3)
                {
                    stRes.push(str);
                }
                str.clear();//str清空
            }
            else//没遇到/， 则更新str
            {
                str += path[i];
            }
        }

        str.clear();
        if(stRes.empty())
            str += '/';
        else
        {
            while(!stRes.empty())
            {
                stTmp.push(stRes.top());
                stRes.pop();
            }
            while(!stTmp.empty())
            {
                str += '/';
                str += stTmp.top();
                stTmp.pop();
            }
        }

        return str;
    }

    int judgeC(string str)//0 or 1 means invalid 2 means 'pop' 3 means 'push'
    {
        int res = 0;
        if(str.length() == 0)
            res = 0;
        else if(str.length() == 1 && str[0] == '.')
            res = 1;
        else if(str.length() == 2 && str[0] == '.' && str[1] == '.')
            res = 2;
        else
            res = 3;
        return res;
    }
};

三.柱形图中最大的矩形（时间复杂度高，耗时，不清晰）

84.题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

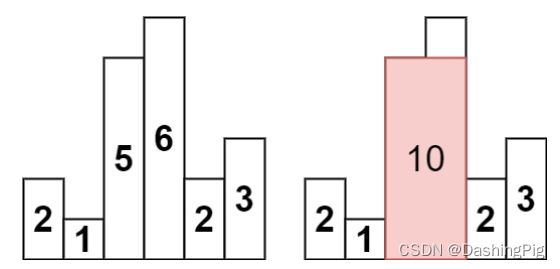
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

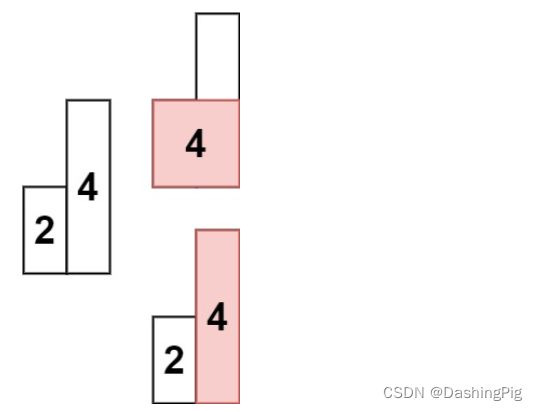
输入： heights = [2,4]
输出： 4

提示：

1 <= heights.length <=105
0 <= heights[i] <= 104

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

思想：使用栈记录高度和位置，矩形的高度由最矮的高度决定！
每次入栈，若当前高<栈顶高，则前面比我高的都作废
高度栈从栈底到栈顶，值递增，栈顶每次出来，清算一遍

数据结构如下：
一个高度栈stH，一个位置栈stL
一个maxS,记录目前已知最大矩形面积

原则：
当前面积和最大面积比较，更新
1.special state,如果栈空且当前高不为0时，（当前面积和最大面积比较），入栈
2.special state,如果当前高0且栈不空， 前面全部清算
3.special state,如果当前高0且栈空，不干
4.如果当前高<栈顶高，边处理和清算边出栈直到 (栈空 || 当前高>=栈顶高)，入栈
5.如果当前高>=栈顶高，入栈

special state,结束时，栈不空，全部清算
special state,结束时，栈空，返回结果
处理：s = (i-栈顶坐标+1)*min(栈顶高, 当前高), 然后若s > maxS, maxS = s;
全部清算：边出栈边处理，直到栈空

反思：
当进入情况4，入栈的应该是a（当前高，最后一个出栈元素的坐标）+b（当前高，当前坐标），因为除了要考虑以当前为开始的清算过程，也要考虑以当前为尾巴的清算过程；

如果只考虑a的情况，对于下列例子无法通过（问题出在最后一个柱子的清算过程）
[0,1,0,2,1,0,1,3,2,1,2,1]
结果输出： 5
答案输出： 6
（此错误已修正）

此外，我的思路不够清晰，代码冗余（不确定栈传过去是引用还是复制）耗时1小时构思，1小时处理细节，最后的AC情况时间复杂度只超过了百分之4的用户。
我使用局部->整体思路，逐步解决问题，大问题分解小问题思路总是很好用。

时间复杂度：o(n)
	因为每一次入栈一次（最坏情况2次），出栈一次（最坏情况2次），共n次；
空间复杂度：o(n)
	因为道理同上；

代码

//思想：使用栈记录高度和位置，矩形的高度由最矮的高度决定！
//每次入栈，若当前高<栈顶高，则前面比我高的都作废
//高度栈从栈底到栈顶，值递增，栈顶每次出来，清算一遍

//数据结构如下：
//一个高度栈stH，一个位置栈stL
//一个maxS,记录目前已知最大矩形面积

//原则：
//当前面积和最大面积比较，更新
//1.special state,如果栈空且当前高不为0时，（当前面积和最大面积比较），入栈
//2.special state,如果当前高0且栈不空， 前面全部清算
//3.special state,如果当前高0且栈空，不干
//4.如果当前高<栈顶高，边处理和清算边出栈直到 (栈空 || 当前高>=栈顶高)，入栈
//5.如果当前高>=栈顶高，入栈

//special state,结束时，栈不空，全部清算
//special state,结束时，栈空，返回结果
//处理：s = (i-栈顶坐标+1)*min(栈顶高, 当前高), 然后若s > maxS, maxS = s;
//全部清算：边出栈边处理，直到栈空

//细节如下：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> stH, stL;
        int maxS = 0;

        for(int i = 0; i <= heights.size()-1; ++i)
        {
            if(heights[i] > maxS)//当前小柱面积和最大面积比较，如果大于，则更新最大面积
                maxS = heights[i];
            if(stH.empty() && heights[i] != 0)//栈空且当前高不为0，则入栈
            {
                stH.push(heights[i]);
                stL.push(i);
            }

            else if(heights[i] == 0 && !stH.empty())//special state，当前高是0且栈不空，清算
            {
                int hTmp = 0, lTmp = 0;
                hTmp = stH.top();
                lTmp = stL.top();
                stH.pop();
                stL.pop();
                while(!stH.empty())
                {   
                    int s = (lTmp-stL.top()+1)*min(stH.top(), hTmp);//处理
                    if(s > maxS)
                        maxS = s;
                    
                    stH.pop();
                    stL.pop();
                }
            }

            else if(heights[i] == 0 && stH.empty());//当前高是0且栈空，啥也不干

            else if(heights[i] < stH.top())//当前高<栈顶高， 边处理和清算边出栈直到当前高>=栈顶高或栈空
            {
                int hTmp = 0, lTmp = 0;//清算准备(1)
                hTmp = stH.top();
                lTmp = stL.top();
                int tmp = 0;//存放栈顶元素的坐标准备(2)
                int s = 0;//面积准备
                while(1)
                {
                    if(stH.empty() || heights[i] >= stH.top())//直到(栈空 || 当前高>=栈顶高)
                        break;
                    tmp = stL.top();//存放栈顶元素坐标(2)

                    s = (i-stL.top()+1)*min(stH.top(), heights[i]);//边处理
                    if(s > maxS)
                        maxS = s;

                    s = (lTmp-stL.top()+1)*min(stH.top(), hTmp);//边清算(1)
                    if(s > maxS)
                        maxS = s;
                    
                    stH.pop();//边出栈
                    stL.pop();
                }
                
                if(!stH.empty())//清算收尾(1)
                {
                    s = (lTmp-stL.top()+1)*min(stH.top(), hTmp);
                    if(s > maxS)
                        maxS = s;
                }

                stH.push(heights[i]);//入栈,为了清算时以此为起点
                stL.push(tmp);
                stH.push(heights[i]);//入栈，为了清算时以此为终点
                stL.push(i);
            }
            else if(heights[i] >= stH.top())//当前高>=栈顶高，入栈
            {   
                stH.push(heights[i]);//入栈
                stL.push(i);
            }
            
        }

        //结束时，栈空，不清算
        if(stH.empty())
            return maxS;

        //special state,结束时，栈不空，全部清算
        int hTmp = 0, lTmp = 0;
        hTmp = stH.top();
        lTmp = stL.top();
        stH.pop();
        stL.pop();
        while(!stH.empty())
        {           
            int s = (lTmp-stL.top()+1)*min(stH.top(), hTmp);//处理
            if(s > maxS)
                maxS = s;

            stH.pop();
            stL.pop();
        }

        return maxS;
    }
};

四.最大矩形

85.题目

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

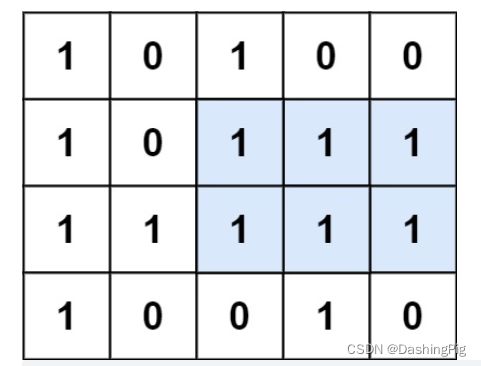
输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：6
解释：最大矩形如上图所示。

示例 2：
输入：matrix = []
输出：0

示例 3：
输入：matrix = [[“0”]]
输出：0

示例 4：
输入：matrix = [[“1”]]
输出：1

示例 5：
输入：matrix = [[“0”,“0”]]
输出：0

提示：

rows == matrix.length
cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] 为 ‘0’ 或 ‘1’

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximal-rectangle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

思路：二维->一维（柱状图）， 栈
我：越想越复杂，没想出来，看了一眼答案，发现这个问题就是柱状图的升维版本，我没看出来啊啊啊
明明柱状图做出来了，却没发现它们两者的联系，我是大傻瓜

反思：
对于复杂问题：局部->整体
对于多维问题：一维->多维

数据结构：
一个存放高的栈stH，一个存放坐标的栈stL，一个存放历史高的vector容器（）
maxS存放当前最大柱形面积

细节如下：
比较当前高和maxS，更新
1.当栈空且高为0，不做
2.当栈空且高不为0,入栈
3.当栈不空且高为0,清算
4.当栈不空且当前高>=栈顶高，入栈
5.当栈不空且当前高<栈顶高，边处理边清算，边出栈直到 栈空或当前高>=栈顶高, 入栈
结束时，如果栈不空，清算
处理公式：s = (j-stL.top()+1)*min(stH.top(), curH), if(s > maxS) maxS = s;

时间复杂度：o(mn)
	因为是84题柱状图矩形情况外加一个m次循环
空间复杂度：o(n)
	因为是84题柱状图矩形情况外加一个记录历史高度的vector容器vHis,实际为2*n

代码

//思路：二维->一维（柱状图）， 栈
//我：越想越复杂，没想出来，看了一眼答案，发现这个问题就是柱状图的升维版本，我没看出来啊啊啊
//明明柱状图做出来了，却没发现它们两者的联系，我是大傻瓜

//反思：
//对于复杂问题：局部->整体
//对于多维问题：一维->多维度

//数据结构：
//一个存放高的栈stH，一个存放坐标的栈stL，一个存放历史高的vector容器（）
//maxS存放当前最大柱形面积

//细节如下：
//比较当前高和maxS，更新
//1.当栈空且高为0，不做
//2.当栈空且高不为0,入栈
//3.当栈不空且高为0,清算
//4.当栈不空且当前高>=栈顶高，入栈
//5.当栈不空且当前高<栈顶高，边处理边清算，边出栈直到 栈空或当前高>=栈顶高, 入栈
//结束时，如果栈不空，清算
//处理公式：s = (j-stL.top()+1)*min(stH.top(), curH), if(s > maxS) maxS = s;

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        //special state
        if(matrix.size() == 0)
            return 0;
        //数据结构准备，两个栈，一个容器，一个结果数
        stack<int> stH, stL;
        vector<int> vHis(matrix[0].size(), 0);
        int maxS = 0;
        //开始计算
        for(int i = 0; i <= matrix.size()-1; ++i)
        {
            for(int j = 0; j <= matrix[0].size()-1; ++j)
            {
                if(matrix[i][j] == '1' && 1+vHis[j] > maxS)
                    maxS = 1+vHis[j];
                if(stH.empty() && matrix[i][j] == '0')
                    vHis[j] = 0;//更新
                else if(stH.empty() && matrix[i][j] == '1')
                {
                    int curH = ++vHis[j]; //获取真实高，并更新

                    stH.push(curH);//入栈
                    stL.push(j);
                }
                else if(matrix[i][j] == '0')
                {
                    vHis[j] = 0;//更新

                    //清算
                    int s = 0;
                    int hTmp = stH.top();
                    int lTmp = stL.top();
                    stH.pop();
                    stL.pop();
                    while(!stH.empty())
                    {
                        s = (lTmp-stL.top()+1)*min(stH.top(), hTmp);
                        if(s > maxS) 
                            maxS = s;
                        
                        stH.pop();
                        stL.pop();
                    } 
                }
                else//m[][] == 1且栈不空
                {
                    int curH = ++vHis[j]; 
                    if(curH >= stH.top())//当前高>=栈顶高
                    {
                        stH.push(curH);//入栈
                        stL.push(j);
                    }
                    else if(curH < stH.top())//当前高<栈顶高
                    {
                        //边处理，边清算，边出栈直到栈空或者当前高>=栈顶高
                        int tmp = 0;//存放位置
                        int s = 0;

                        s = (j-stL.top()+1)*min(stH.top(), curH);//边处理(2)
                        if(s > maxS) 
                            maxS = s;

                        int hTmp = stH.top();
                        int lTmp = stL.top();
                        tmp = stL.top();//记录位置
                        stH.pop();
                        stL.pop();
                        while(!stH.empty())
                        {
                            if(curH >= stH.top())
                                break;

                            s = (lTmp-stL.top()+1)*min(stH.top(), hTmp);//边清算(1)
                            if(s > maxS) 
                                maxS = s;

                            s = (j-stL.top()+1)*min(stH.top(), curH);//边处理(2)
                            if(s > maxS) 
                                maxS = s;
                        
                            tmp = stL.top();//记录位置
                            stH.pop();
                            stL.pop();
                        } 
                        //栈不空，清算结尾
                        if(!stH.empty())
                        {
                            s = (lTmp-stL.top()+1)*min(stH.top(), hTmp);//边清算(1)
                            if(s > maxS) 
                                maxS = s;
                        }

                        //入栈
                        stH.push(curH);
                        stL.push(tmp);
                        stH.push(curH);
                        stL.push(j);
                    }
                }
                
            }

            //栈不空，则清算
            if(!stH.empty())
            {
                int s = 0;
                int hTmp = stH.top();
                int lTmp = stL.top();
                stH.pop();
                stL.pop();
                while(!stH.empty())
                {
                    s = (lTmp-stL.top()+1)*min(stH.top(), hTmp);
                    if(s > maxS) 
                        maxS = s;
                        
                    stH.pop();
                    stL.pop();
                } 
            }
        }

        return maxS;
    }
};

五.二叉树展开为链表

114.题目

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

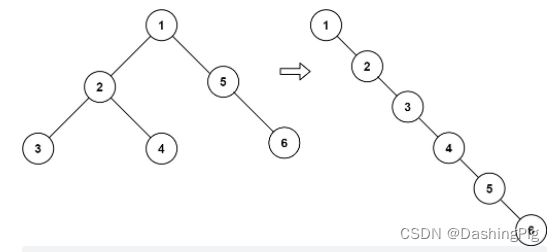
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？（不会）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

思想：先序遍历 + 栈 = 压栈顺序 右->左->中
每次有元素进入stRes,进行封尾操作
stHis空时，所有元素都没有孩子

数据结构：一个栈stRes，存底到顶存逆序结果(右左中)；一个栈stHis，存历史结点（中右左）
一个函数judge()，决定$封尾操作是左空(0)还是右空(1)， 并执行封尾

细节如下：
1.遍历右，如果 有孩子， 压中到stHis， 直到没孩子，压中到stRes ($令stHis右空或左空)2.出栈，如果左空，压中到stRes($)， 直到有左孩子，当前元素入stHis 回到1
循环1.2直到stHis空
注意：压入stRes的元素a的父母不再指向a

代码

//思想：先序遍历 + 栈 = 压栈顺序 右->左->中
//每次有元素进入stRes,进行封尾操作
//stHis空时，所有元素都没有孩子

//数据结构：一个栈stRes，存底到顶存逆序结果(右左中)；一个栈stHis，存历史结点（中右左）
//一个函数judge()，决定$封尾操作是左空(0)还是右空(1)， 并执行封尾

//细节如下：
//1.遍历右，如果 有孩子， 压中到stHis， 直到没孩子，压中到stRes ($令 stHis 右空或左空)
//2.出栈，  如果 左空， 压中到stRes($)， 直到有左孩子，当前元素入stHis 回到1
//循环1.2直到stHis空
//注意：压入stRes的元素a的父母不再指向a

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        stack<TreeNode*> stHis, stRes;

        //specail state, it is empty
        if(!root)
            return;
        
        //formal state, it is not empty
        TreeNode* p = root;
        
        do{
            //1.右大操作
            while(p->right || p->left)
            {
                stHis.push(p);
                if(p->right)
                    p = p->right;
                else
                    p = p->left;
            }
            stRes.push(p);
            if(!stHis.empty())
                judge(stHis.top(), p);
            else
                break;

            //2.左大操作
            do{
                p = stHis.top();//出栈
                stHis.pop();

                if(!p->left)//当左空
                {
                    stRes.push(p);
                    if(!stHis.empty())
                        judge(stHis.top(), p);
                    else
                        break;
                }  
                else//当左不空
                {
                    stHis.push(p);
                    p = p->left;
                    break;
                }   
            }while(1);
            
        }while(!stHis.empty());

        while(!stRes.empty())
        {
            p = stRes.top();
            stRes.pop();

            if(!stRes.empty())
                p->right = stRes.top();
        }
    }
    void judge(TreeNode* parent, TreeNode* child)
    {
        if(parent->right == child)
            parent->right = nullptr;
        else
            parent->left = nullptr;
    }
};