克鲁斯卡尔(Kruskal)算法(严蔚敏C语言)

克鲁斯卡尔算法(Kruskal)

​ 克鲁斯卡尔算法是求连通网的最小生成树的另一种方法。与普里姆算法不同，它的时间复杂度为O（eloge）（e为网中的边数），所以，适合于求边稀疏的网的最小生成树 。 ——百度百科

一、基本思想：

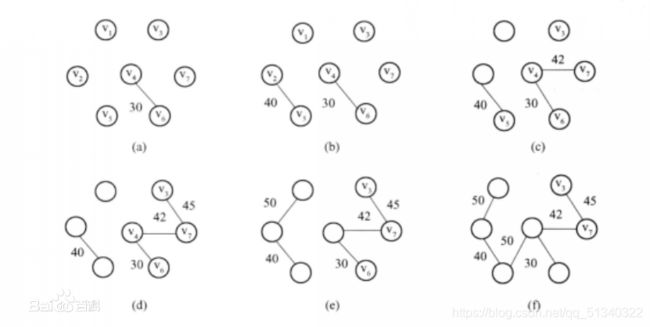
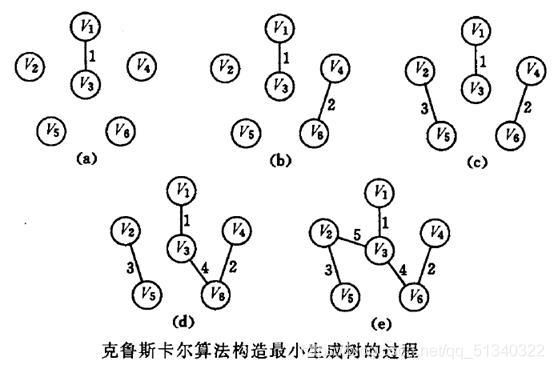
​ 克鲁斯卡尔（Kruskal）算法从另一途径求网的最小生成树。其基本思想是：假设连通网G=（V，E），令最小生成树的初始状态为只有n个顶点而无边的非连通图T=（V，{}），概述图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点分别在T中不同的连通分量上，则将此边加入到T中；否则，舍去此边而选择下一条代价最小的边。依此类推，直至T中所有顶点构成一个连通分量为止 。

看不懂长篇大论没事，就记住这：哪里权(值)小连哪里，n个点连n-1个边，不能连成一个环

不成环说明：根据集合的思想，一般来说，克鲁斯卡尔从边出发，但本质上来说，与图中的顶点有关，每次从一个已连通集合某点出发，连接一个未并入的点，使被连点并入已连通集合。如果说就因为选中的两点间权值最小，考虑连接，发现连接了就构成成环回路了，这说明这两个点已经都在已连通的集合里了，这时候并入就没有意义，所以不选能成环的两点

二、中间过程：

​ 实际上，就是先选择权值最小的边，对于有n个顶点的图来说，选择n-1条边即可。另外，不能存在环。

什么，这还不懂？小心这：QAQ

其实，数据结构是门理论课，关于最小生成树的克鲁斯卡尔算法知道怎么连线就行了。。。

三、代码实现：

1. 重要准备：

要用到两个重要的辅助数组，分别为Edge数组和Vexset数组

struct EdgeM
{
    vextype Head;//一般vextype为char型
    vextype Tail;
    int lowcost;
}Edge[N];

其中，Head是边的一段，Tail是边的另一端，两点中间的路径所带的权为lowcost，按权排序后即可使用。

int Vexset[N];

辅助数组，用于排除Kruskal出现有环的情况(有环是不对滴)

思路：在Vexset数组中分别查找v1和v2所在的连通分量vs1和vs2，进行判断

1. 如果vs1 != vs2 表明两个点处于不同的连通分量，输出此边，合并vs1和vs2两个连通分量

2. 如果vs1和vs2相等，表明所选两个顶点属于同一个连通分量，那么则舍去此边选择下一个权值最小的边

2. 核心代码：

在严蔚敏《数据结构》一书中，Sort()函数未给出，即最重要的排序没给出，这时，我们需要手写Sort函数给Edge数组进行排序。常见两种方法：

1. 使用c++STL中的sort(头文件为algorithm)，sort()函数有三个参数，前两个参数是必写的，分别是数组起始地址，结束地址。有时候第三个参数不写，就默认从小到大，实际上第三个参数为比较参数。例如：int a[5] = {1, 5, 9, 2, 4};

   sort(a, a + 5) => 1， 2， 4， 5， 9。当然因为a数组是int型的，sort函数的编写人员对c语言的数据类型比较熟悉，所以，只要是一个常见数据类型，比如int, float, double…数组都可以排序，但是对于自己定义的struct数组，sort不知道如何比较，比如：

   struct 
   {
      int a, b; 
   }Arr[10];
   

   这时候sort不知道按照a的大小来还是按照b的大小来排序，所以要手写比较函数，即sort()函数的第三个参数。

   bool cmp(const EdgeM &a, const EdgeM &b)
   {
       return a.lowcost < b.lowcost;//从小到大排序
   }
   void Sort(AMGraph G)
   {
       sort(Edge, Edge + G.arcnum, cmp);
   }
   

2. 重载 < 号，让sort知道什么是Edge数组的 < 号

   struct EdgeM
   {
       vextype Head;
       vextype Tail;
       int lowcost;
       bool operator < (const EdgeM &p)
       {
           return lowcost < p.lowcost;
       }
   }Edge[N];
   
   void Sort(AMGraph G)
   {
       sort(Edge, Edge + G.arcnum);//即可
   }
   

   当然，也可以把重载函数写在结构体外边

   struct EdgeM
   {
       vextype Head;
       vextype Tail;
       int lowcost;
   }Edge[N];
   
   bool operator < (const EdgeM &p1, const EdgeM &p2)
   {
       return p1.lowcost < p2.lowcost;
   }
   
   void Sort(AMGraph G)
   {
       sort(Edge, Edge + G.arcnum);//也可
   }
   

3. 完整代码：

下面展示完整代码：

建议直接收藏并关注本蒟蒻，嘻嘻

#include 

using namespace std;

const int N = 200, M = 0x7fffffff;
typedef char vextype;

typedef struct 
{
    vextype vex[N];
    int arcs[N][N];
    int vexnum, arcnum;
}AMGraph;

struct EdgeM
{
    vextype Head;
    vextype Tail;
    int lowcost;
}Edge[N];
//书上伪代码为：
/*
struct
{
    vextype Head;
    vextype Tail;
    arctype lowcost;
}Edge[arcnum];//这里arcnum是一个变量，应该动态开辟数组内存，为了方便，数量为N;
*/

int Vexset[N];//辅助数组，用于排除Kruskal出现环的情况
/*思路：在Vexset数组中分别查找v1和v2所在的连通分量vs1和vs2，进行判断
1. 如果vs1 != vs2 表明两个点处于不同的连通分量，输出此边，合并vs1和vs2两个连通分量
2. 如果vs1和vs2相等，表明所选两个顶点属于同一个连通分量，那么则舍去此边选择下一个权值最小的边
*/
int minspatree_matrix[N][N];//最小生成树的邻接矩阵
pair <int, int> ans[N];

void CreatGraph(AMGraph &G)
{
    cout << "请输入顶点数目和边的数目：" << endl;
    cin >> G.vexnum >> G.arcnum;
    
    for (int i = 0; i < G.vexnum; ++ i) {
        for (int j = 0; j < G.vexnum; ++ j)
            G.arcs[i][j] = M;
    }
    cout << "请输入所有顶点名称：" << endl;
    for (int i = 0; i < G.vexnum; ++ i) cin >> G.vex[i];

    cout << "请输入所有边的权值：" << endl;
    int x, y, w;
    for (int i = 0; i < G.arcnum; ++ i) {
        cin >> x >> y >> w;
        G.arcs[x][y] = G.arcs[y][x] = w;
        Edge[i] = {G.vex[x], G.vex[y], w};
    }
}
/*下面是对书中Sort函数的实现*/
bool cmp(const EdgeM &a, const EdgeM &b)
{
    return a.lowcost < b.lowcost;
}

void Sort(AMGraph G)
{
    sort(Edge, Edge + G.arcnum, cmp);
}

int Locate(AMGraph G, vextype v)
{
    for (int i = 0; i < G.arcnum; ++ i) {
        if (G.vex[i] == v) return i;
    }
    return -1;
}

void MiniSpanTree(AMGraph &G)
{
    Sort(G);
    int cnt = 0;
    for (int i = 0; i < G.vexnum; ++ i) Vexset[i] = i;//初始时，每个点为一个单独的连通分量                                                 
    for (int i = 0; i < G.arcnum; ++ i) {//*这层循环是有问题的，选边的总数为G.vexnum - 1
        int v1 = Locate(G, Edge[i].Head);//而不是遍历所有的边，但是书上面就是这么写的
        int v2 = Locate(G, Edge[i].Tail);//仅供基础学习基本思路。

        int vs1 = Vexset[v1];
        int vs2 = Vexset[v2];

        if (vs1 != vs2)
        {
            cout << Edge[i].Head << ' ' << Edge[i].Tail << endl;
            ans[cnt ++] = {Locate(G, Edge[i].Head), Locate(G, Edge[i].Tail)};//c++11标准，c99会警告，分开赋值即可
            for (int j = 0; j < G.vexnum; ++ j) {
                if (Vexset[j] == vs2) Vexset[j] = vs1;
            }
        }
    }
    // for (int i = 0; i < G.vexnum - 1; ++ i) {
    //     int x = ans[i].first, y = ans[i].second;//将已经选择完成的边，放入最小生成树矩阵中
    //     minspatree_matrix[x][y] = minspatree_matrix[y][x] = G.arcs[x][y];
    // }
}

int main()
{
    AMGraph G;
    CreatGraph(G);
    MiniSpanTree(G);
    /*输出原始的矩阵*/
    // for (int i = 0; i < G.vexnum; ++ i) {
    //     for (int j = 0; j < G.vexnum; ++ j)
    //         cout << G.arcs[i][j] << ' ';
    //     cout <
    // }
    /*输出最小生成树的邻接矩阵*/
    // for (int i = 0; i < G.vexnum; ++ i) //cout << Vexset[i] << ' ';
    // {
    //     for (int j = 0; j < G.vexnum; ++ j)
    //         cout << minspatree_matrix[i][j] << ' ';
    //     cout << endl;
    // }

    system("pause");

    return 0;
}
/*
测试用例：
4 5
A B C D
0 1 3
0 3 4
1 2 6
2 3 7
1 3 5
*/

总结

上面的代码仅供学习，书上面的代码肯定是有漏洞的，下面给出一份正确无误的，可过oj的代码：
不用vexset数组作为集合了，这样太慢了会超时，用并查集路径压缩维护关系速度更快
题目：

问题： 给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。
求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G
的最小生成树。

输入格式 第一行包含两个整数 n 和 m。
接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式 共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围
1≤n≤10^5,
1≤m≤2∗10^5,
图中涉及边的边权的绝对值均不超过 1000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例： 6

概述样例： 按边权从小到大排序
1 2 1
1 3 2
2 3 2
1 4 3
3 4 4
四个顶点则选3条边，分别为是1 2、 1 3、1 4
权值和为：1 + 2 + 3 = 6
不选2 3是因为前两次选择使2 3被包含进来了，否则会成环。

克鲁斯卡尔算法：

#include 
#include 

using namespace std;

const int N = 100010, INF = 0x3f3f3f3f;

int n, m;

typedef struct
{
    int Head;
    int Tail;
    int lowcost;
}EdgeM;

EdgeM Edge[2* N];

int p[N];

int find(int x)
{
    if (p[x] == x) return x;
    return p[x] = find(p[x]);
}

bool operator < (const EdgeM &p1, const EdgeM &p2)
{
    return p1.lowcost < p2.lowcost;
}

int MiniSpanTree()
{
    sort(Edge + 1, Edge + m + 1);
    int res = 0, cnt = 0;
    for (int i = 1; i <= n; ++ i)  p[i] = i;//初始时，每个点为一个单独的连通分量                                                 
    for (int i = 1; i <= m && cnt != n - 1; ++ i) {
        int v1 = Edge[i].Head, v2 = Edge[i].Tail;
        int vs1 = find(v1), vs2 = find(v2);
        if (vs1 != vs2)
        {
            res += Edge[i].lowcost; ++ cnt;
            p[vs1] = find(vs2);
        }
    }
    if (cnt == n - 1) return res;
    return INF;
}

int main()
{
    cin >> n >> m;
    int x, y, w;
    for (int i = 1; i <= m; ++ i) {
        cin >> x >> y >> w;
        Edge[i] = {x, y, w};
    }
    int t = MiniSpanTree();
    if (t < INF)  cout << t << '\n';
    else cout << "impossible" << '\n';
    
    return 0;
}

---

THEEND…