【数据结构】归并排序和计数排序(排序的总结)
目录
一,归并排序的递归
二,归并排序的非递归
三,计数排序
四,排序算法的综合分析
一,归并排序的递归
基本思想:
归并采用的是分治思想,是分治法的一个经典的运用。该算法先将原数据进行拆分,此步骤与二叉树的拆分思想一样(因此,运用递归比较简单),然后将最终拆分后的每一小部分排序,最后将已有序的子序列进行合并,得到完全有序的序列,其中关键为要使每个分割后的子序列有序,再使子序列段间有序,即合并有序序列。以上中将两个有序表合并成一个有序表称为二路归并。思想图如下(以升序为例):
上图中,先以中间数据为界,将一堆数据进行不断分解,当分解完全后,再进行合并,而在合并时其实就是边排序边合并。由于在排序中要改动原数据,因此,我们可再创建一个数组进行改动,然后将改动后的数据赋值给原数据块即可,代码和导图如下:
代码运行导图
导图中,先取中间值,以此下标为界限分开左右区间,然后再不断递归分割,最后一次分割为leftbegin == leftend,rightbegin == rightend,此时就要进行排序组合,组合完子序列后即可往原序列就行赋值,此为一趟遍历,然后递归就不断进行返回,即不断就行合并排序,最终全部元素有序。
归并代码:
void MergeFunction(int* a, int* nums, int n, int begin, int end) {
//当分割区间为1个数据时就要停止分割,即此时begin == end
if (begin == end) {
return;
}
int middle = (begin + end) / 2;//中间数据,控制界限
//在左区间[begin, middle]和右区间[middle + 1, end]进行不断分割
MergeFunction(a, nums, n, begin, middle);
MergeFunction(a, nums, n, middle + 1, end);
//分割后,下面是进行左右区间的排序
int leftbegin = begin, leftend = middle;
int rightbegin = middle + 1, rightend = end;
int insert = begin;
//以下是进行分割后的排序
while (leftbegin <= leftend && rightbegin <= rightend) {
if (a[leftbegin] < a[rightbegin]) {
nums[insert++] = a[leftbegin++];
}
else {
nums[insert++] = a[rightbegin++];
}
}
while (leftbegin <= leftend) {
nums[insert++] = a[leftbegin++];
}
while (rightbegin <= rightend) {
nums[insert++] = a[rightbegin++];
}
//拷贝数组
memcpy(a + begin, nums + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n) {
int* nums = (int*)malloc(sizeof(int) * n);//此数组用于临时放入数据
if (!nums) {
perror("nums malloc");
exit(-1);
}
MergeFunction(a, nums, n, 0, n - 1);
free(nums);
}
样例代码,将以下中数组a进行排序(升序):
#include
#include
#include
void MergeFunction(int* a, int* nums, int n, int begin, int end) {
//当分割为1个时就要停止分割,即此时begin == end
if (begin == end) {
return;
}
int middle = (begin + end) / 2;//中间数据,控制界限
//在左区间[begin, middle]和右区间[middle + 1, end]进行不断分割
MergeFunction(a, nums, n, begin, middle);
MergeFunction(a, nums, n, middle + 1, end);
//分割后,下面是进行左右区间的排序
int leftbegin = begin, leftend = middle;
int rightbegin = middle + 1, rightend = end;
int insert = begin;
//以下是进行分割后的排序
while (leftbegin <= leftend && rightbegin <= rightend) {
if (a[leftbegin] < a[rightbegin]) {
nums[insert++] = a[leftbegin++];
}
else {
nums[insert++] = a[rightbegin++];
}
}
while (leftbegin <= leftend) {
nums[insert++] = a[leftbegin++];
}
while (rightbegin <= rightend) {
nums[insert++] = a[rightbegin++];
}
//拷贝数组
memcpy(a + begin, nums + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n) {
int* nums = (int*)malloc(sizeof(int) * n);//此数组用于临时放入数据
if (!nums) {
perror("nums malloc");
exit(-1);
}
MergeFunction(a, nums, n, 0, n - 1);
free(nums);
}
int main() {
int a[] = { 10,6,7,1,3,9,4,2 };
MergeSort(a, sizeof(a) / sizeof(int));
for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
fprintf(stdout, "%d ", a[i]);
}
puts("");
return 0;
} 运行图:
二,归并排序的非递归
我们平常将递归改成非递归首先可能想起要运用栈结构,但是,我们先理一下归并的思路,当我们不断分割时确实可以用栈结构来控制区间,但是当回并时可能就比较麻烦,因此,本人不建议用栈结构,不是不可以,是有更好的方法。
归并递归时是将数据不断进行二分,即分治思想,当用非递归时,我们可设置一个间隔gap,以次模仿递归时的二分思想,每次循环结束后将此间隔乘二即可。非递归思路导图如下:
由以上图不难发现,此种非递归合并的思路与递归合并的思路有些不太一样,此种非递归的思想是一旦有了一个间隔值后,就一次性的将全部数据按照此间隔值进行间隔归并。
非递归归并的时候要注意一个点,当数据个数为奇数时,不难发现,左区间[leftbegin,leftend]无影响,但右区间[rightbegin,rightend]将会溢出,此时情况,如果rightbegin溢出的话那么可之间退出,因为据上图中所示,每一趟归并时就相当于将下一趟的左区间就排列有序了;如果rightend溢出的话,直接令rightend为最后一个元素的下标进行归并排序即可。当数据个数为偶数时不会出现溢出情况。
代码如下:
void MergeSortNonR(int* a, int n) {
int* nums = (int*)malloc(sizeof(int) * n);
//gap是每次隔离的间隔,也可理解为将要排序的元素个数
int gap = 1;//控制gap间据的大小
while (gap < n) {
for (int i = 0; i < n; i += 2 * gap) {
//以gap为间距分割,左区间[leftbegin,leftend]共有gap个元素
int leftbegin = i, leftend = i + gap - 1;
//以gap为间距分割,当原始数有偶数的元素时,右区间[rightbegin,rightend]有gap个元素
int rightbegin = i + gap, rightend = i + gap + gap - 1;
int insert = i;
//以下是当元素个数为奇数时的情况
if (rightbegin >= n) {
break;
}
if (rightend >= n) {
rightend = n - 1;
}
//开始进行排序,排列的数据区间为[leftbegin, rightend]
while (leftbegin <= leftend && rightbegin <= rightend) {
if (a[leftbegin] < a[rightbegin]) {
nums[insert++] = a[leftbegin++];
}
else {
nums[insert++] = a[rightbegin++];
}
}
while (leftbegin <= leftend) {
nums[insert++] = a[leftbegin++];
}
while (rightbegin <= rightend) {
nums[insert++] = a[rightbegin++];
}
//将排列的区间[leftbegin, rightend]进行拷贝,因为leftbegin和rightbegin都已改变,所以不能用这两个数据
memcpy(a + i, nums + i, sizeof(int) * (rightend - i + 1));
}
gap *= 2;
}
free(nums);
}
样例代码,将以下中数组a进行排序(升序):
#include
#include
#include
void MergeSortNonR(int* a, int n) {
int* nums = (int*)malloc(sizeof(int) * n);
//gap是每次隔离的间隔,也可理解为将要排序的元素个数
int gap = 1;
while (gap < n) {
for (int i = 0; i < n; i += 2 * gap) {
//leftbegin和leftend理解为在gap区间内的元素
int leftbegin = i, leftend = i + gap - 1;
//rightbegin和rightend可理解为在预排序gap区间的后面的元素
int rightbegin = i + gap, rightend = i + gap + gap - 1;
int insert = i;
//以下是当元素为奇数时的情况
if (rightbegin >= n) {
break;
}
if (rightend >= n) {
rightend = n - 1;
}
//开始进行排序,排列的数据区间为[leftbegin, rightend]
while (leftbegin <= leftend && rightbegin <= rightend) {
if (a[leftbegin] < a[rightbegin]) {
nums[insert++] = a[leftbegin++];
}
else {
nums[insert++] = a[rightbegin++];
}
}
while (leftbegin <= leftend) {
nums[insert++] = a[leftbegin++];
}
while (rightbegin <= rightend) {
nums[insert++] = a[rightbegin++];
}
//将排列的区间[leftbegin, rightend]进行拷贝,因为leftbegin和rightbegin都以改变,所以不能用这两个数据
memcpy(a + i, nums + i, sizeof(int) * (rightend - i + 1));
}
gap *= 2;
}
free(nums);
}
int main() {
int a[] = { 10,6,7,1,3,9,4,2 };
MergeSortNonR(a, sizeof(a) / sizeof(int));
for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
fprintf(stdout, "%d ", a[i]);
}
puts("");
return 0;
} 运行图:
运算发的效率:
最后我们来谈论一下此算法的效率,不难发现,由于此算法中运用的是二分思想,所以时间复杂度为O(nlogn),空间复杂度O(n)。由此可见,此算法的效率也算高,跟快排不同的是,此算法与原始数据的初始位置并无太大影响,效率比较稳定。
三,计数排序
计数排序可从字面意思理解,通过数组的下标来计数来间接实现数据的排序。首先,我们需设置一个数组,此数组是通过下标来进行计数的,原数据中最大数据个数为max - min + 1(max是原数据的最大元素,min是原数据最小的元素),即幅度range在区间[0,max - min]中,因此,我们可设置数组大小为max - min + 1(不包括重复数组,重复的数据我们可用相同下标对应的数值记录出现的次数),即最大下标为max - min(记录最大元素的位置),下标的设置思想为:原数据 - min。然后将设置数组初始化为0(也可选举其它值,但选举0是最为简单的),0表示原数据中没有此元素,然后幅度range遍历,一旦存在此元素加1,表示出现元素的次数,最后将其设置数组中出现过元素的下标加上min赋给原数据即可得到有序序列,思维导图如下:
代码如下(以升序为例):
void CountSort(int* a, int n) {
//以下是寻找最大值max和最小值min,为了后面确定幅度range
int min = a[0], max = a[n - 1], j = 0;
for (int i = 0; i < n; i++) {
if (a[i] > max) {
max = a[i];
}
if (a[i] < min) {
min = a[i];
}
}
//最大元素个数为range,下标为“原数据 - min”
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
memset(count, 0, sizeof(int) * range);//初始化0,表元素个数为0
for (int i = 0; i < n; i++) {
//用计数数组count的有序下标来进行有序计数,记录出现过元素的次数
count[a[i] - min]++;//注意: 不能count[a[i] - min] = 1,因为可能有重复数据
}
//最后遍历,一旦存在此值将,下标 + min即为数据
for (int i = 0; i < range; i++) {
while (count[i]--) {
a[j++] = i + min;
}
}
free(count);
}
代码演示(以升序为例):
#include
#include
#include
void CountSort(int* a, int n) {
//以下是寻找最大值max和最小值min,为了后面确定幅度range
int min = a[0], max = a[n - 1], j = 0;
for (int i = 0; i < n; i++) {
if (a[i] > max) {
max = a[i];
}
if (a[i] < min) {
min = a[i];
}
}
//最大元素个数为range,下标为“原数据 - min”
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
memset(count, 0, sizeof(int) * range);//初始化0,表元素个数为0
for (int i = 0; i < n; i++) {
//用计数数组count的有序下标来进行有序计数,记录出现过元素的次数
count[a[i] - min]++;//注意: 不能count[a[i] - min] = 1,因为可能有重复数据
}
//最后遍历,一旦存在此值将,下标 + min即为数据
for (int i = 0; i < range; i++) {
while (count[i]--) {
a[j++] = i + min;
}
}
free(count);
}
int main() {
int a[] = { 10,6,7,1,3,9,4,2 };
CountSort(a, sizeof(a) / sizeof(int));
for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
fprintf(stdout, "%d ", a[i]);
}
puts("");
return 0;
} 运行图:
计数效率与注意要点:
计数排序的时间复杂度为O(range + n) ,空间复杂度为O(range),效率是非常高的,因为无论什么排序算法,最好的时间效率无非是O(n),而计数排序的时间复杂度达到O(range + n),已经非常接近O(n)。无论是希尔排序,堆排序,快速排序还是归并排序都达不到此效率,但此算法也不是最优选择,因为此算法完全可以说是那空间换时间,当range非常大时会消耗很大的空间,而且由于此算法是运用数组下标进行间接排序的,因此,此算法只能对整型排序,不能对其它数据类型进行排序,使得此算法有了很大的局限性。
四,排序算法的综合分析
1,算法的效率分析
排序算法的效率不能只根据时间复杂度和空间复杂度,因为两者的计算都是取最好情况和最坏情况进行概率的综合分析,最终取平均,比如排序的原始序列不同,快排算法,直接插入算法和冒泡算法的效率比较大,直接插入和冒泡最好的情况都是有序的情况,此时时间复杂度都为O(n),而快排最好的情况是基准值每次在中间,此时时间复杂度为O(nlogn)。但大多数情况下,我们根本预测不了原始序列和原始数据,所以在大多数情况下可直接根据时间复杂度和空间复杂度直接判断,若对数据比较敏感的话就要根据具体情况进行具体分析,从而选取最优算法。
2,算法的稳定性
稳定性:相同的数据排序后,相对位置是否发生变化,若两者之间的相对位置没有发生变化,则算法稳定,发生变化,算法不稳定。
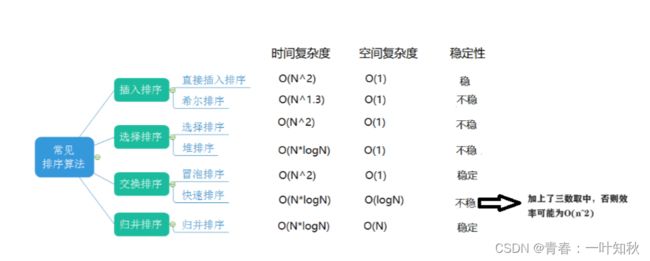
在初学情况下,稳定性确实不算太重要,但是在后面深入学习系统操作和程序等先后顺序就显得尤为重要,例如,一个程序要对学生进行考试排名,其中高成绩出现了两个99分的和两个98分,这时两个99分的学生谁先排入第一名和两个98分的学生谁排入第三名就显得尤为重要,这就要求排序算法的稳定性。最后总结一下各个算法的效率和稳定性:
其中计数排序没必要加上,因为计数局限性太强了,在后面的学习中基本用不到,并且提醒一下,以上中的算法效率和稳定性千万不要死记,因为之前说过,这些算法的效率基本都不稳定,不同的情况可能出现不同的效率,而某些算法的设计不同可能稳定,也可能不稳定,因此,理解算法的思想和如何实现尤为重要。