数据结构之LinkedList与链表
目录
1.LinkedList的特点和存在意义
2.LinkedList的简单使用
2.1.LinkedList的构造
2.2.常见方法
2.3.遍历
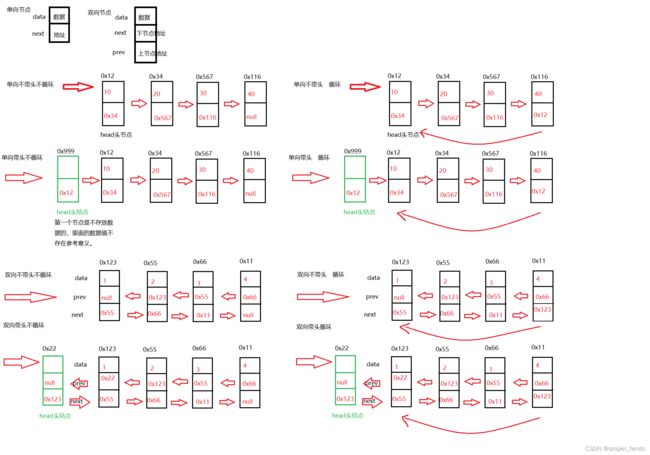
3.链表结构
4.简单实现
4.1单向无头不循环链表
4.2.双向无头不循环链表
5.ArrayList与LinkedList的不同
1.LinkedList的特点和存在意义
LinkedList的底层是双向链表结构，由于链表没有将元素存储在连续的空间中，元素存储在单独的节 点中，然后通过引用将节点连接起来了，因此在在任意位置插入或者删除元素时，不需要搬移元素，效率比较高。这就是LinkedList的意义所在。
注意以下四点：
1. LinkedList实现了 List 接口。
2. LinkedList的底层使用了双向链表。
3. LinkedList没有实现 RandomAccess 接口，因此 LinkedList 不支持随机访问。
4. LinkedList的任意位置插入和删除元素时效率比较高，时间复杂度为 O(1)。
2.LinkedList的简单使用
2.1.LinkedList的构造
| 方法 | 说明 |
|
LinkedList ()
|
无参构造
|
|
public LinkedList(Collection c)
|
使用其他集合容器中元素构造 List
|
public static void main(String[] args) {
// 构造一个空的LinkedList
List list1 = new LinkedList<>();
List list2 = new java.util.ArrayList<>();
list2.add("JavaSE");
list2.add("JavaWeb");
list2.add("JavaEE");
// 使用ArrayList构造LinkedList
List list3 = new LinkedList<>(list2);
} 2.2.常见方法
|
方法
|
说明 |
|
boolean add (E e)
|
尾插 e
|
|
void add (int index, E element)
|
将 e 插入到 index 位置
|
|
boolean addAll (Collection c)
|
尾插 c 中的元素
|
|
E remove (int index)
|
删除 index 位置元素
|
|
boolean remove (Object o)
|
删除遇到的第一个 o
|
|
E get (int index)
|
获取下标 index 位置元素
|
|
E set (int index, E element)
|
将下标 index 位置元素设置为 element
|
|
void clear ()
|
清空
|
|
boolean contains (Object o)
|
判断 o 是否在线性表中
|
|
int indexOf (Object o)
|
返回第一个 o 所在下标
|
|
int lastIndexOf (Object o)
|
返回最后一个 o 的下标
|
|
List |
截取部分 list
|
2.3.遍历
public static void main(String[] args) {
LinkedList list = new LinkedList<>();
list.add(1); // add(elem): 表示尾插
list.add(2);
list.add(3);
list.add(4);
list.add(5);
list.add(6);
list.add(7);
System.out.println(list.size());
// foreach遍历
for (int e:list) {
System.out.print(e + " ");
}
System.out.println();
// 使用迭代器遍历---正向遍历
ListIterator it = list.listIterator();
while(it.hasNext()){
System.out.print(it.next()+ " ");
}
System.out.println();
// 使用反向迭代器---反向遍历
ListIterator rit = list.listIterator(list.size());
while (rit.hasPrevious()){
System.out.print(rit.previous() +" ");
}
System.out.println();
} 3.链表结构
链表是一种物理存储结构上非连续 存储结构，数据元素的 逻辑顺序 是通过链表中的 引用链接 次序实现的 。
需注意：
1.链表在物理地址上不一定连续，在逻辑上连续。
2.节点一般在堆上申请出来的。
3.从堆上申请的空间是按照一定的策略分配的，两次申请的空间不一定连续。
4.简单实现
接下来我来实现单向无头不循环链表和双向无头不循环链表两种结构，由于是简单实现，我们的数据类型是基本数据类型的整形类型，但实际LinkedList的底层实现包括了基本数据类型和引用数据类型，同时底层是双向链表结构。
4.1单向无头不循环链表
在单向链表常用方法的模拟中需要注意下面几个常用的方式，定义新的节点，参与循环，修改节点next的指向，及时保存节点信息再进行修改。如头插法需要判断链表是否为空，如果为空，只需将head节点引用插入节点并置空next;如果不为空，则需将插入节点的next指向head,再将head指向插入节点。尾插法需要定义cur节点引用，通过循环将cur指向链表最后一个节点，在进行节点指向的修改，只需将cur节点的next指向插入节点，切记一定要将插入的最后一个节点的next置空。其他的方法思路大同小异，大家仔细研究一下就明白了。
class Node {
public int val;
public Node next;//类型是Node null
public Node(int val) {
this.val = val;
}
}
public class SingleLinkedList {
public Node head;//定义到这是因为它是链表的头
public int usedSize;//记录当前链表节点个数
//穷举法创建链表
public void createList() {
Node node1 = new Node(12);
Node node2 = new Node(23);
Node node3 = new Node(34);
Node node4 = new Node(45);
Node node5 = new Node(56);
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
this.head = node1;
this.usedSize = 5;
}
//打印链表
public void myToString() {
Node cur = this.head;//不用head的原因是防止head最后指向空
//循环条件不能为cur.next!=null,否则最后一个节点值不打印
while(cur!=null){
System.out.print(cur.val+" ");
cur = cur.next;
}
System.out.println();
}
//重载打印方法(从指定节点开始打印)
public void myToString(Node newHead) {
Node cur = newHead;
//循环条件不能为cur.next!=null,否则最后一个节点值不打印
while(cur!=null){
System.out.print(cur.val+" ");
cur = cur.next;
}
System.out.println();
}
//查找是否包含关键字key在链表中
public boolean contains(int key) {
Node cur = this.head;
while(cur!=null){
//如果key不是整形，用equals比较
if(cur.val==key) {
return true;
}
cur = cur.next;
}
return false;
}
//得到单链表的长度(尝试不使用usedSize),如果使用usedSize直接返回即可(优点时间复杂度小)
public int size() {
Node cur = this.head;
int num = 0;
while(cur!=null){
num++;
cur = cur.next;
}
return num;
}
//头插法
public void addFirst(int data) {
Node node = new Node(data);
if(this.head==null) {
this.head = node;
}else {
node.next = this.head;
this.head = node;
}
this.usedSize++;
}
//尾插法
public void addLast(int data){
Node node = new Node(data);
if(this.head == null) {
this.head = node;
}else {
Node cur = this.head;
while (cur.next!=null) {
cur = cur.next;
}
//cur指向最后一个节点
cur.next = node;
}
this.usedSize++;
}
//查找index的前一个节点并返回
public Node searchIndex(int index) {
Node cur = head;
for (int i = 0; i < index-1; i++) {
cur = cur.next;
}
return cur;
}
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data) {
Node node = new Node(data);
if(index<0||index>this.usedSize){
throw new RuntimeException("index不合法!");
}
if(index == 0){
addFirst(data);
return;
}
if(index == this.usedSize){
addLast(data);
return;
}
Node cur = searchIndex(index);
node.next = cur.next;
cur.next = node;
this.usedSize++;
}
//找到key关键字的前一个节点
public Node searchKey(int key) {
Node cur = this.head;
while(cur.next!=null){
if(cur.next.val == key){
return cur;
}
cur = cur.next;
}
return null;
}
//删除第一次出现关键字为key的节点
public void remove(int key){
//链表为空
if(this.head == null) {
return;
}
//头结点就是要求删除的节点
if(this.head.val == key){
this.head = this.head.next;
this.usedSize--;
return;
}
Node cur = searchKey(key);
if(cur == null){
throw new RuntimeException("不存在要删除的节点!");
}
Node del = cur.next;
cur.next = del.next;
this.usedSize--;
}
//删除所有值为key的节点
public void removeAllKey(int key){
if(this.head == null){
return;
}
Node cur = this.head.next;
Node prev = this.head;
while(cur!=null){
if(cur.val == key){
prev.next = cur.next;
cur = cur.next;
this.usedSize--;
}else{
prev = cur;
cur = cur.next;
}
}
if(this.head.val == key){
this.head = this.head.next;
this.usedSize--;
}
}
//清空链表
public void clear(){
Node cur = this.head;
while (cur!=null){
Node curNext = cur.next;
cur.next = null;
cur = curNext;
}
this.head = null;
this.usedSize = 0;
}
public void clear1() {
//暴力写法
this.head = null;
this.usedSize = 0;
}
}4.2.双向无头不循环链表
由于多定义了尾节点和前驱信息你，双向链表的实现思路就比单向链表更简单一点，在插入元素和删除元素中，不需要定义更多的节点引用，灵活利用next和prev就能实现插入和删除。因此LinkedList比ArrayList更适合频繁插入和删除数据的场景。
class ListNode{
public int val;//值
public ListNode next;//后继信息
public ListNode prev;//前驱信息
public ListNode(int val) {
this.val = val;
}
}
public class DoubleLinkedList {
public ListNode head;//头节点
public ListNode last;//尾节点
//头插法
public void addFirst(int data){
ListNode cur = new ListNode(data);
if(this.head == null){
this.head = cur;
this.last = cur;
return;
}
cur.next = this.head;
head.prev = cur;
head = cur;
}
//尾插法
public void addLast(int data){
ListNode cur = new ListNode(data);
if(this.last == null){
this.head = cur;
this.last = cur;
return;
}
this.last.next = cur;
cur.prev = this.last;
this.last = cur;
}
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data){
if(index<0||index>size()) {
throw new RuntimeException("index不合法！");
}
if(index == 0){
addFirst(data);
return;
}
if(index == size()){
addLast(data);
return;
}
ListNode node = new ListNode(data);
ListNode ret = findIndex(index);
node.next = ret;
node.prev = ret.prev;
ret.prev.next = node;
ret.prev = node;
}
//查找下标为index的节点
public ListNode findIndex(int index) {
ListNode cur = this.head;
while(index!=0){
cur = cur.next;
index--;
}
return cur;
}
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key){
ListNode cur = this.head;
while(cur!=null){
if(cur.val==key){
return true;
}
}
return false;
}
//删除第一次出现关键字为key的节点
public void remove(int key){
ListNode cur = this.head;
while(cur!=null){
if(cur.val == key){
//删头节点
if(cur == this.head){
this.head = head.next;
//判断是不是只有一个节点
if(this.head!=null){
this.head.prev = null;
}
//删其他节点(中间节点、尾节点)
}else{
cur.prev.next = cur.next;
//判断是不是尾节点
if(cur.next!=null){
cur.next.prev = cur.prev;
}else{
this.last = last.prev;
}
}
return;
}else{
cur = cur.next;
}
}
}
//删除所有值为key的节点
public void removeAllKey(int key){
ListNode cur = this.head;
while(cur!=null){
if(cur.val == key){
//删头节点
if(cur == this.head){
this.head = head.next;
//判断是不是只有一个节点
if(this.head!=null){
this.head.prev = null;
}
//删其他节点(中间节点、尾节点)
}else{
cur.prev.next = cur.next;
//判断是不是尾节点
if(cur.next!=null){
cur.next.prev = cur.prev;
}else{
this.last = last.prev;
}
}
}
cur = cur.next;
}
}
//得到单链表的长度
public int size(){
int count = 0;
ListNode cur = this.head;
while(cur!=null){
count++;
}
return count;
}
public void myToString(){
ListNode cur = this.head;
while(cur!=null){
System.out.print(cur.val+" ");
}
System.out.println();
}
public void clear(){
ListNode cur = this.head;
while(cur!=null){
ListNode curNext = cur.next;
//如果是引用类型的数据则cur.val = null
cur.prev = null;
cur.next = null;
cur = curNext;
}
this.head = null;
this.last = null;
}
}
5.ArrayList与LinkedList的不同
| 不同 | ArrayList | LinkedList |
|
存储空间上
|
物理上一定连续
|
逻辑上连续，但物理上不一定连续
|
|
随机访问
|
支持O(1)
|
不支持： O(N)
|
|
头插
|
需要搬移元素，效率低 O(N)
|
只需修改引用的指向，时间复杂度为 O(1)
|
|
插入
|
空间不够时需要扩容
|
没有容量的概念
|
|
应用场景
|
元素高效存储 + 频繁访问
|
任意位置插入和删除频繁
|