数据结构：二叉树（3）：相关oj题目
二叉树oj题的续
目录
102. 二叉树的层序遍历 - 力扣（LeetCode）
236. 二叉树的最近公共祖先 - 力扣（LeetCode）
方法1
方法2
105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）
106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）
606. 根据二叉树创建字符串 - 力扣（LeetCode）
144. 二叉树的前序遍历 - 力扣（LeetCode）
非递归的后序遍历
102. 二叉树的层序遍历 - 力扣（LeetCode）
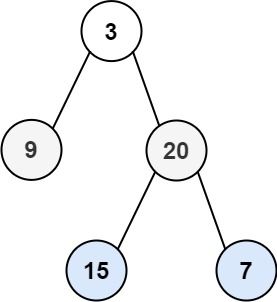
给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。
示例 1：
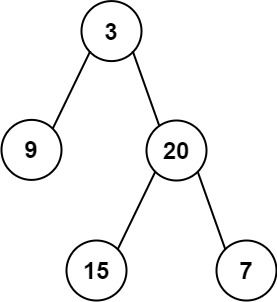
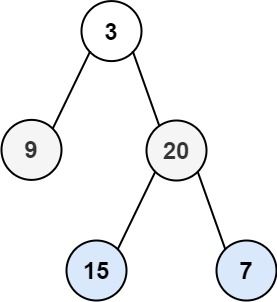
输入：root = [3,9,20,null,null,15,7] 输出：[[3],[9,20],[15,7]]
示例 2：
输入：root = [1] 输出：[[1]]
示例 3：
输入：root = [] 输出：[]
提示：
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
--------------------------------------------------------------------------------------------------------------------------------
先不看题目，我们自己在本地模拟一个层序遍历出来
层序遍历：从上到下，从左到右遍历
从上到下遍历：前序/中序/后序
从左到右遍历：使用队列，把根结点放进队列，出队列；然后把左右子树也放进去，依次出队列
设置一个cur来遍历队列，这个cur = 出队列的元素，出完队列后把这个cur（也就是刚出队列的元素）的左右子树加入队列
void levelOrder(TreeNode root){
if(root == null){
return ;
}
Queue queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode cur = queue.poll();
System.out.println(cur.val + " ");
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right!= null){
queue.offer(cur.right);
}
}
} ---------------------------------------------------------------------------------------------------------------------------------
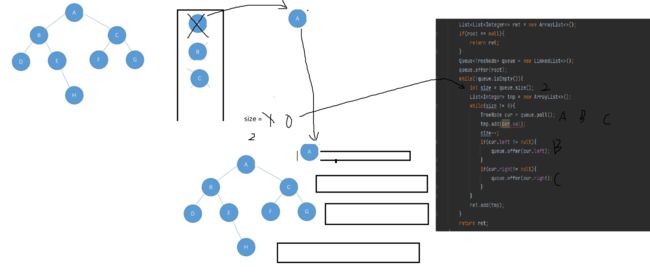
我们回到题目上来，题目给的函数要求我们返回一个二维数组
问题来了，如何存储每一层的结点到list当中？如何确定一层中有多少个结点？
我们可以定义一个size来记录整个队列的大小，创建一个tmp数组。（这俩是全局变量）
设置一个循环（循环条件是size!=0），每次弹出cur位置的元素后把这个元素放到tmp数组里面，size再--
然后把cur左子树和右子树加进队列
上面定义的size是全局变量，所以在循环里面，就算你把左右子树入队，在size没有--到0的时候是不会退出循环的，所以不用担心加入新元素会导致死循环的情况
每一层列表创建完后，把所有的列表扔到ret列表里面
class Solution {
public List> levelOrder(TreeNode root) {
List> ret = new ArrayList<>();
if(root == null){
return ret;
}
Queue queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
List tmp = new ArrayList<>();
while(size != 0){
TreeNode cur = queue.poll();
tmp.add(cur.val);
size--;
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right!= null){
queue.offer(cur.right);
}
}
ret.add(tmp);
}
return ret;
}
} 
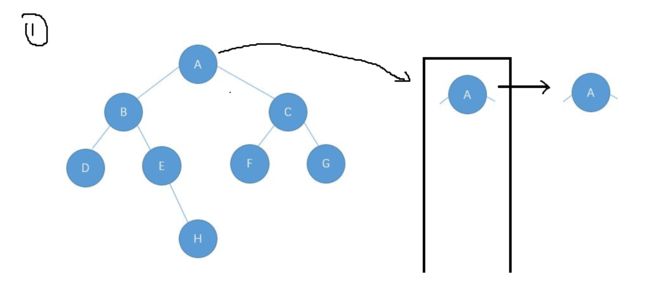
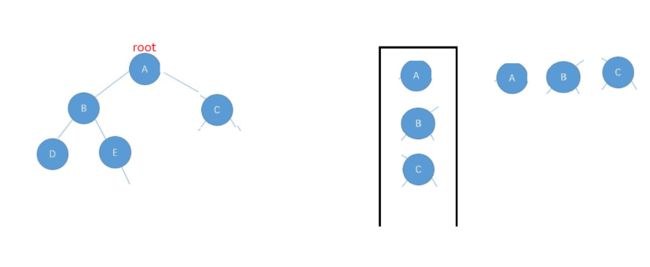
利用层序遍历思想来判断一棵树是不是完全二叉树
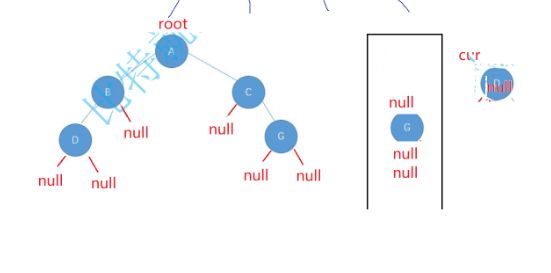
当把队列里面弹出null后整个队列里面都是null，说明这棵树是一颗完全二叉树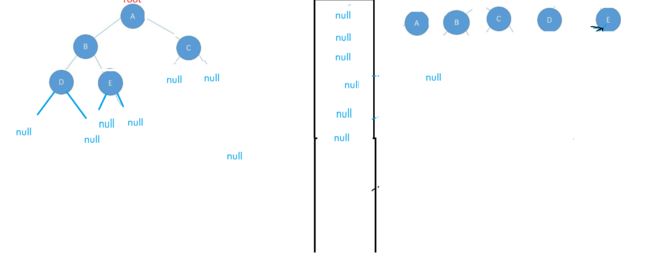
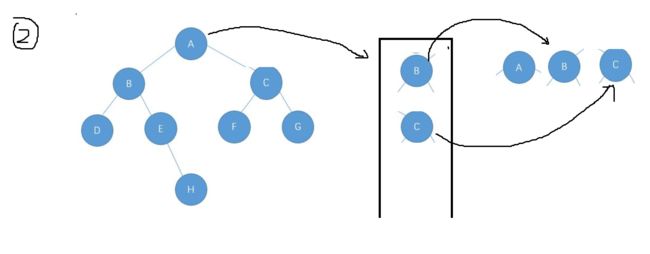
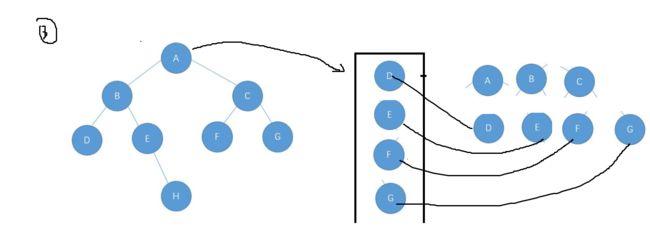
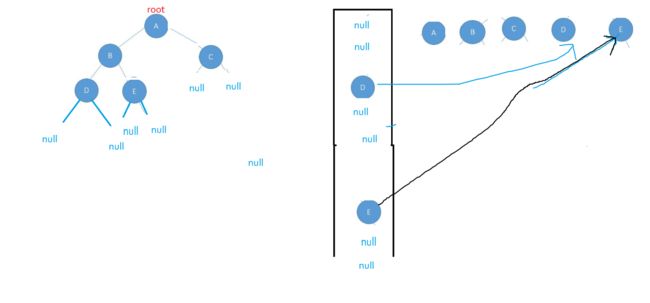
如果不是一棵完全二叉树的话会出现这样的情况
弹出null之后队列里面还有元素G
boolean isCompleteTree(TreeNode root){
if(root == null){
return true;
}
Queue queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode cur = queue.poll();
if(cur!=null){
queue.offer(cur.left);
queue.offer(cur.right);
}else{
break;//结束循环
}
}
//代码走到这是把元素都入队了，包括null
//需要判断队列中是否有空的元素
while(!queue.isEmpty()){
//一个元素一个元素出队来判断是不是空
//把null弹出，如果遇到不是null的元素就返回错误
TreeNode tmp = queue.peek();
if(tmp == null){
queue.poll();
}else{
return false;
}
}
return true;
} 236. 二叉树的最近公共祖先 - 力扣（LeetCode）
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
示例 1：
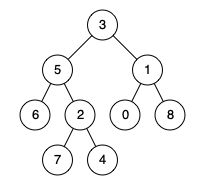
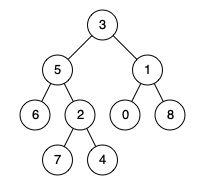
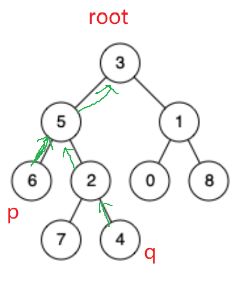
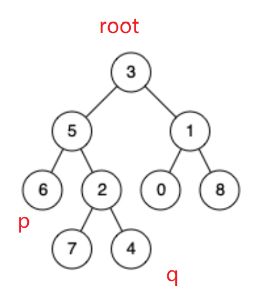
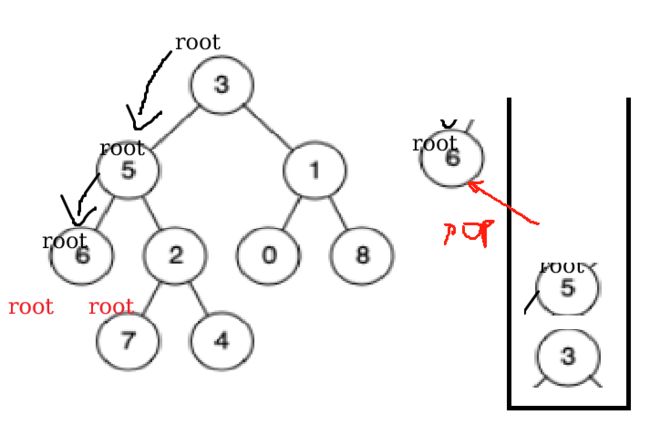
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出：3 解释：节点5和节点1的最近公共祖先是节点 3
示例 2：
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出：5 解释：节点5和节点4的最近公共祖先是节点5。 因为根据定义最近公共祖先节点可以为节点本身。
示例 3：
输入：root = [1,2], p = 1, q = 2 输出：1
提示：
- 树中节点数目在范围
[2, 105]内。 -109 <= Node.val <= 109- 所有
Node.val互不相同。 p != qp和q均存在于给定的二叉树中。
方法1
分为三种情况
情况1
情况2
情况3
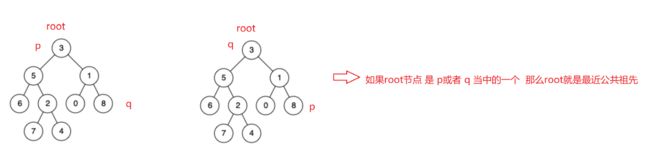
root遍历这棵树，遇到p或者q就返回
如果两边的返回都不为空，root就是最近公共祖先
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null){
return root;
}
//情况1
if(root == p || root == q){
return root;
}
TreeNode leftTree = lowestCommonAncestor(root.left,p,q);
TreeNode rightTree = lowestCommonAncestor(root.right,p,q);
//情况2
if(leftTree != null && rightTree != null){
return root;
//情况3
}else if(leftTree != null){
return leftTree;
}else{
return rightTree;
}
}
---------------------------------------------------------------------------------------------------------------------------------
方法2
假设p = 6，q等于4，从自身出发往根结点方向遍历，遍历到相同的结点就是最近公共祖先
其实相当于求链表的交点
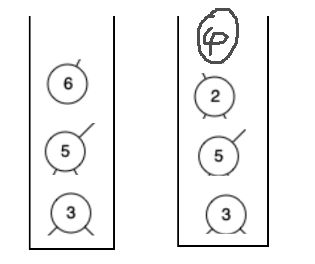
我们把p和q的父结点（包括自己）全部拿出来，分别放到两个栈里面
长度不一样就先把长的栈里面先拿出元素直到两个栈等长，然后每次各自拿出一个元素进行比较，不同继续拿，相同了就终止并返回最后拿出来的元素
现在问题来了：如何存储从根结点到p或者q的路径上的所有结点，还有如何找到p和q？
我们使用一个函数getPath(root,node,stack)，每次遍历到一个结点就把这个结点扔到栈里面
如果遍历到root = node，就返回true
判断如果左树没有结点，右树没有结点，则当前的root就不是路径上的结点，我们返回false并把这个root元素从栈中弹出
private boolean getPath(TreeNode root, TreeNode node, Stack stack){
if(root == null || node == null){
return false;
}
stack.push(root);
if(root == node){
return true;
}
//判断左子树有没有结点
boolean flg = getPath(root.left, node, stack);
if(flg == true){
return true;
}
//判断右子树有没有结点
boolean flg2 = getPath(root.right, node, stack);
if(flg2 == true){
return true;
}
//都没有结点就把root元素弹出来并返回false退到这个root的父结点
stack.pop();
return false;
} public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
Stack stackP = new Stack<>();
Stack stackQ = new Stack<>();
getPath(root,p,stackP);
getPath(root,q,stackQ);
int sizep = stackP.size();
int sizeq = stackQ.size();
if(sizep > sizeq){
int size = sizep - sizeq;
while(size != 0){
stackP.pop();
size--;
}
}else{
int size = sizeq - sizep;
while(size != 0){
stackQ.pop();
size--;
}
}
//走到这，两个栈当中元素一样多
//接下来判断两个栈的栈顶元素一不一样，一样就返回，不一样就分别弹出
while(!stackP.isEmpty() && !stackQ.isEmpty()){
if(stackP.peek() == stackQ.peek()){
return stackP.peek();
}else{
stackP.pop();
stackQ.pop();
}
}
return null;
} 105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
前序遍历：根，左，右
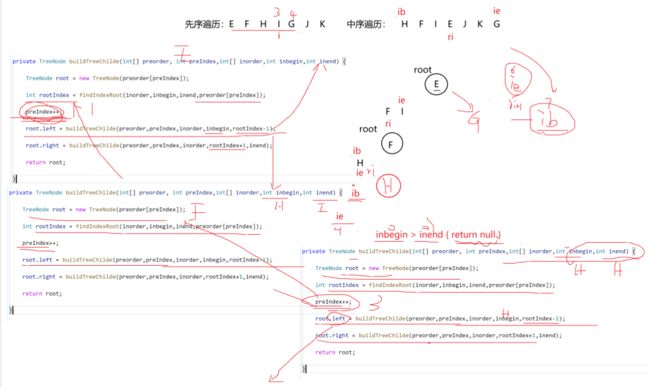
private TreeNode buildTreeChild(int[] preorder, int preIndex,
int[] inorder, int inbegin, int inend){
TreeNode root = new TreeNode(preorder[preIndex]);
//找到根结点在中序遍历中的位置
int rootIndex = findIndexRoot(inorder,inbegin,inend,preorder[preIndex]);
preIndex++;
root.left = buildTreeChild(preorder,preIndex,inorder,inbegin,rootIndex-1);
root.left = buildTreeChild(preorder,preIndex,inorder,rootIndex+1,inend);
return root;
} private int findIndexRoot(int[] inorder, int inbegin, int inend, int key){
//这里的<=是因为inend = rootIndex - 1
for(int i = inbegin; i<=inend;i++){
if(inorder[i] == key){
return i;
}
}
return -1;
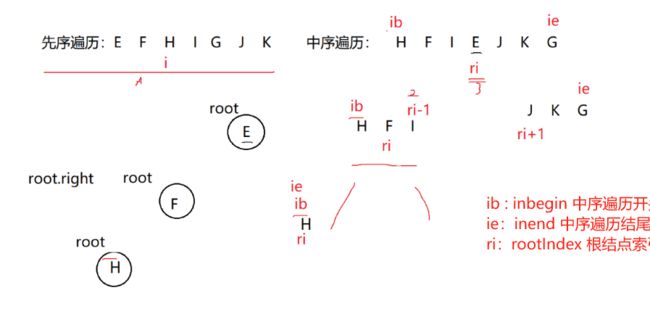
}第一个问题：什么时候退出循环呢？
我们分析一下
拿左子树举例，当preindex遍历到H结点的时候，ie的值为-1，这不被我们允许，所以我们规定inbegin>inend时就返回空
第二个问题：preIndex是一个局部变量，当我们找到结点左右的树为空时，我们要回去上一个结点，当返回到E结点时，preIndex其实等于1，它到不了4
那就在上面把preIndex定义成全局变量
class Solution {
public int preIndex ;
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildTreeChilde(preorder,inorder,0,inorder.length-1);
}
private TreeNode buildTreeChilde(int[] preorder,int[] inorder,int inbegin,int inend) {
if(inbegin > inend) {
return null;//没有 左树 或者 没有 右树
}
TreeNode root = new TreeNode(preorder[preIndex]);
int rootIndex = findIndexRoot(inorder,inbegin,inend,preorder[preIndex]);
if(rootIndex == -1) {
return null;
}
preIndex++;
root.left = buildTreeChilde(preorder,inorder,inbegin,rootIndex-1);
root.right = buildTreeChilde(preorder,inorder,rootIndex+1,inend);
return root;
}
private int findIndexRoot(int[] inorder,int inbegin, int inend,int key) {
for(int i = inbegin; i <= inend;i++) {
if(inorder[i] == key) {
return i;
}
}
return -1;
}
}
106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）
给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）
示例 1：
输入：root = [3,9,20,null,null,15,7] 输出：[[15,7],[9,20],[3]]
示例 2：
输入：root = [1] 输出：[[1]]
示例 3：
输入：root = [] 输出：[]
跟前序遍历相反，后序遍历我们把postIndex放到最后一个元素，往前遍历，因为后序遍历最后一个元素就是根结点
问题：先创建左树还是先创建右树？
答案是先创建右树，因为pi往前遍历的结点就在整个树的右树里面
跟上面的题目差不多，就是遍历方式不一样而已
class Solution {
public int postIndex ;
public TreeNode buildTree(int[] inorder, int[] postorder) {
postIndex = postorder.length-1;//注意这一行代码的定义
return buildTreeChilde(postorder,inorder,0,inorder.length-1);
}
private TreeNode buildTreeChilde(int[] postorder,int[] inorder,int inbegin,int inend) {
if(inbegin > inend) {
return null;//没有 左树 或者 没有 右树
}
TreeNode root = new TreeNode(postorder[postIndex]);
int rootIndex = findIndexRoot(inorder,inbegin,inend,postorder[postIndex]);
if(rootIndex == -1) {
return null;
}
postIndex--;
root.right = buildTreeChilde(postorder,inorder,rootIndex+1,inend);
root.left = buildTreeChilde(postorder,inorder,inbegin,rootIndex-1);
return root;
}
private int findIndexRoot(int[] inorder,int inbegin, int inend,int key) {
for(int i = inbegin; i <= inend;i++) {
if(inorder[i] == key) {
return i;
}
}
return -1;
}
}606. 根据二叉树创建字符串 - 力扣（LeetCode）
给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。
空节点使用一对空括号对 "()" 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1：
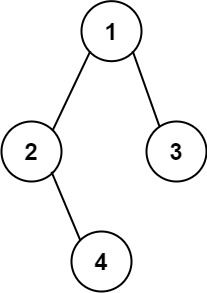
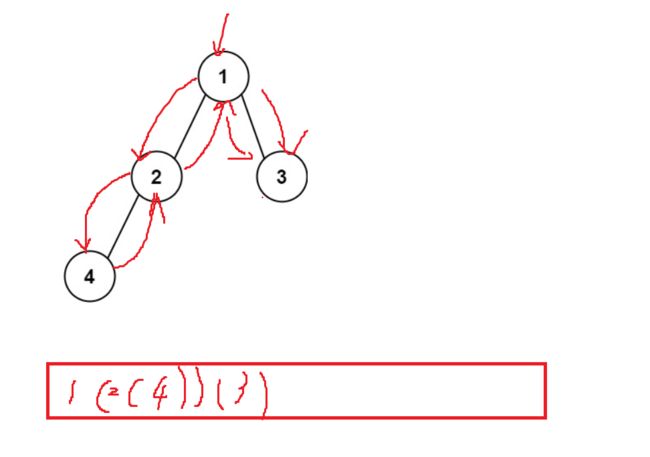
输入：root = [1,2,3,4] 输出："1(2(4))(3)" 解释：初步转化后得到 "1(2(4)())(3()())" ，但省略所有不必要的空括号对后，字符串应该是"1(2(4))(3)" 。
示例 2：
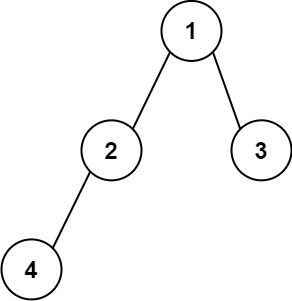
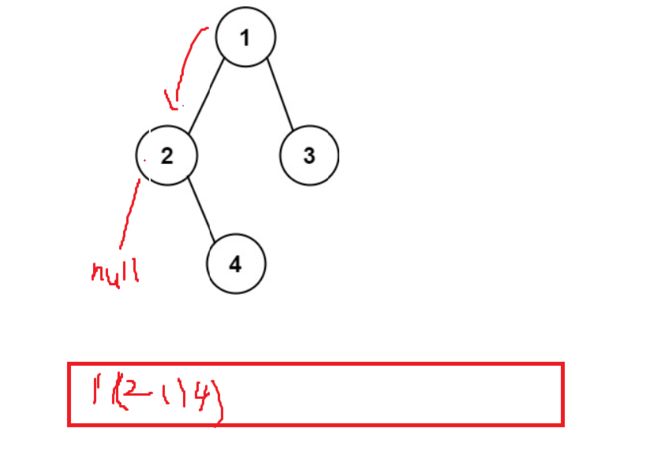
输入：root = [1,2,3,null,4] 输出："1(2()(4))(3)" 解释：和第一个示例类似，但是无法省略第一个空括号对，否则会破坏输入与输出一一映射的关系。
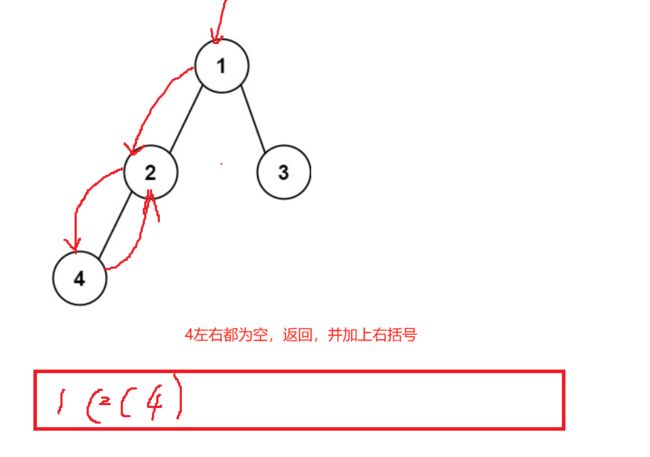
1.根结点直接拼接
2.左边为空并且右边为空的时候什么都不做
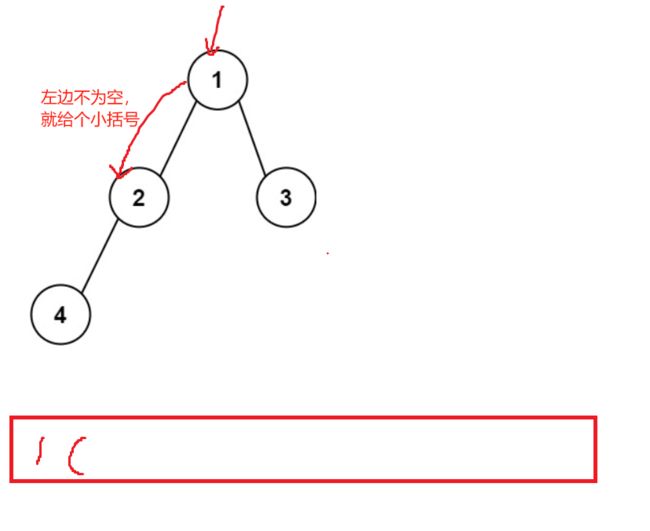
3.左边不为空，右边为空
4.左边为空，右边不为空，直接加上一对小括号
class Solution {
public String tree2str(TreeNode root) {
StringBuilder stringBuilder = new StringBuilder();
tree2strchild(root,stringBuilder);
return stringBuilder.toString();
}
private void tree2strchild(TreeNode t, StringBuilder stringBuilder){
if(t == null){
return ;
}
stringBuilder.append(t.val);
if(t.left != null){
stringBuilder.append("(");
tree2strchild(t.left,stringBuilder);
//遍历到左树为空的时候返回并加上右括号,证明左树已经遍历完了
stringBuilder.append(")");
}else{
//左边为空右边也为空，什么都不做
if(t.right == null){
return ;
//左边为空右边不为空，直接加()
}else{
stringBuilder.append("()");
}
}
//判断右树
if(t.right != null){
stringBuilder.append("(");
tree2strchild(t.right,stringBuilder);
//遍历到右树为空的时候返回并加上右括号,证明右树已经遍历完了
stringBuilder.append(")");
}else{
return;
}
}
}
144. 二叉树的前序遍历 - 力扣（LeetCode）
是不是看着很眼熟，我们之前写的前序遍历是采用递归方法，现在这道题我们采用非递归的方法来做
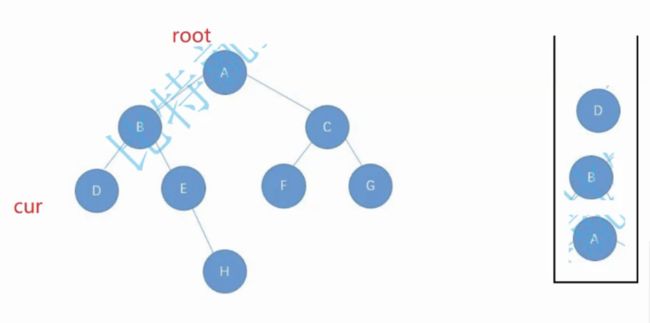
设置一个栈和一个用来遍历的cur，当cur遍历一个元素就加入到栈中，先遍历左子树
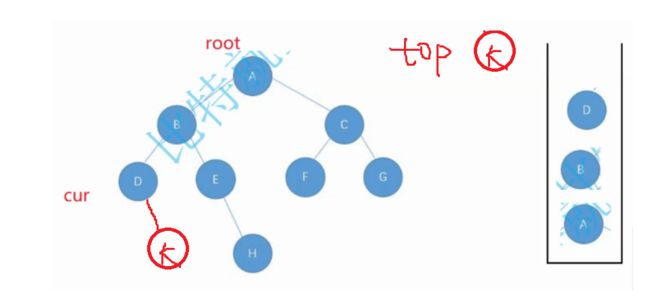
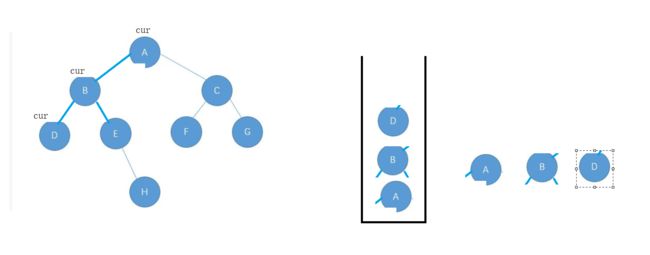继续往下遍历，D左右子树空了，就把D弹出来，交给一个top的变量，cur移到D的右边
D的右边为空，返回B。弹出B，cur遍历到B的右边
注意要先弹出元素cur才能遍历到该元素的右边
void preOrderNor(TreeNode root){
if(root == null) {
return;
}
Stack stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
//前序遍历先打印根
System.out.print(cur.val + " ");
cur = cur.left;
}
TreeNode top = stack.pop();
cur = top.right;
}
} 顺带扯一下中序遍历
1.cur一直往左走，遇到空停止，如果左树走完了就弹出栈顶元素并且打印
2.遍历弹出结点的右子树
void inOrderNor(TreeNode root){
if(root == null) {
return;
}
Stack stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
//这里得先弹出元素再打印
TreeNode top = stack.pop();
System.out.print(top.val + " ");
cur = top.right;
}
} 非递归的后序遍历
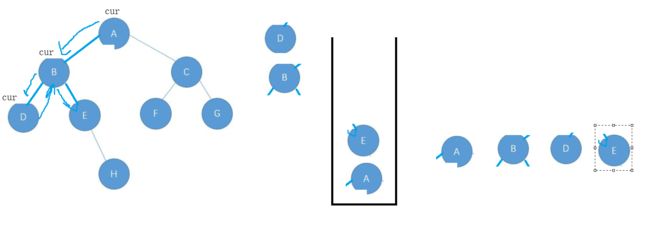
第一步：设置cur遍历左子树，把遍历到的元素放入栈中，但不要打印（因为要遍历完右子树才能打印根）
void postOrderNor(TreeNode root){
if(root == null) {
return;
}
Stack stack = new Stack<>();
TreeNode cur = root;
while (cur != null) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
}
} 第二步：打印D的右子树，我们可以定义一个top先暂时存储此时的栈顶元素D，让cur移到top这里
分成两种情况 ==null 弹出D并打印D
!= null cur就往D的右边走
while(cur != null){
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.peek();
if(top.right == null){
System.out.println(top.val);
stack.pop();
}else{
cur = top.right;
}
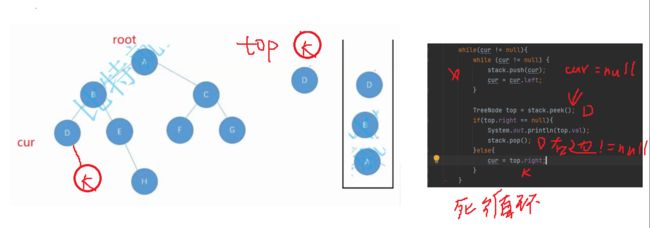
}现在问题来了，假设D左边有一个元素K，把K弹出并打印之后
cur为空，进不了第一个循环，进入top定义语句，找到top = D，再往下走
此时D的右边是K，依旧不为空，又把K弹出来又打印了一遍，这样就陷入了死循环了
那我们可以加入一个prev来记录最新被打印的结点，与此同时，判断top.right == prev
整个代码：
void postOrderNor(TreeNode root){
if(root == null) {
return;
}
Stack stack = new Stack<>();
TreeNode cur = root;
TreeNode prev = null;
while(cur != null || !stack.isEmpty()){
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.peek();
if(top.right == null || top.right == prev){
System.out.println(top.val + " ");
stack.pop();
prev = top;
}else{
cur = top.right;
}
}
}