前缀和与差分算法
前缀和与差分
- 一维前缀和
- 一维差分
- 二维前缀和
- 二维差分
一维前缀和
先看一个例子,假如我们现在有一个数组
arr[]={3,2,5,6,7,8,9,4,2}
现在假如我们要想的得到区间 [ 3 , 6 ],上的数据和,那我们就需要遍历 [ 3 , 6 ] 这个区间进行求和。
代码如下:
#include 假如我们需要多次询问区间和时
#include 它的时间复杂度将会是O(m*n),当数组很长,询问次数很多时,这样的求和方法效率就非常低下。
为了改进这种算法,就引入了前缀和
前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。
合理的使用前缀和与差分,可以将某些复杂的问题简单化。
前缀和公式
sum[i]=arr[i] (i==0)
sum[i]=sum[i-1]+arr[i] (i>0)
这个和高中的数列前n项和是差不多的
对于数组
arr[]={3,2,5,6,7,8,9,4,2}
我们可以根据公式求出他的前缀和数组
sum[]={3,5,10,16,23,31,40,44,46}
当我们要询问区间 [ l , r ] 上的数字和时
sum1=sum[r]-sum[l-1];
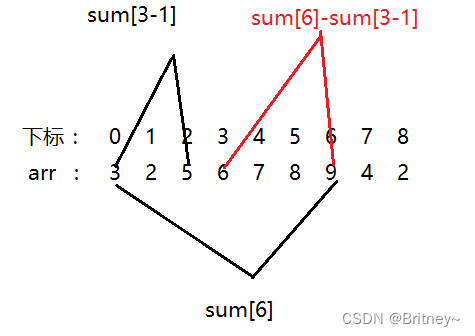
其实原理很好理解,比如我们我要求 [3 , 6 ] 上的区间和
sum[6]=arr[0]+arr[1]+arr[2]+arr[3]+arr[4]+arr[5]+arr[6]
sum[2]=arr[0]+arr[1]+arr[2];
sum[6]-sum[2]=arr[3]+arr[4]+arr[5]+arr[6]
如下图所示·
代码如下:
#include 通过求前缀和,我们可以把原本O(m*n)的时间复杂度化为O(n)
一维差分
还是刚刚的数组
arr[]={3,2,5,6,7,8,9,4,2}
假如我们要对区间 [ 3 , 6 ] 上的数据都加上 m ,我们就需要遍历这个区间。当我们需要多次进行如上操作时,
时间复杂度也将会成为O(m*n)
代码如下:
#include 当数组元素多,操作次数多时,这样的代码也是十低效的。
这样我们就需要引出差分了
差分数组
sub[i]=arr[i]-arr[i-1] (i!=0)
sub[i]=arr[i] (i==0)
对上面的数组求差分可以得到
sub[]={3,-1,3,1,1,1,1,-5,-2};
差分数组的性质
1.对差分数组进行前缀和,就可以的到原数组
分析:
原数组: a1 a2 a3 a4 a5
差分数组:a1 a2-a1 a3-a2 a4-a3 a5-a4
前缀和: a1 a2 a3 a4 a5
2.要对数组区间 [ l, r ] 的数据都加上m时,我们只需要对差分数组的
sub[l]+=m;
sub[r+1]-=m;
即可,所有操作做完后,做前缀和求出原数组即可
注意事项:如果r+1可以超过原数组大小,所以我们可以在开辟sub数组时多开辟一块空间,也可以对超过原数组的情况不做任何处理(不求差分),也是不会影响结果的。
代码如下:
#include 二维前缀和
上面我们讨论了一维数组,但二维数组我们需要怎样处理呢?
如下数组:
int arr[][4] = { {1 ,2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11,12},
{13,14,15, 16} };
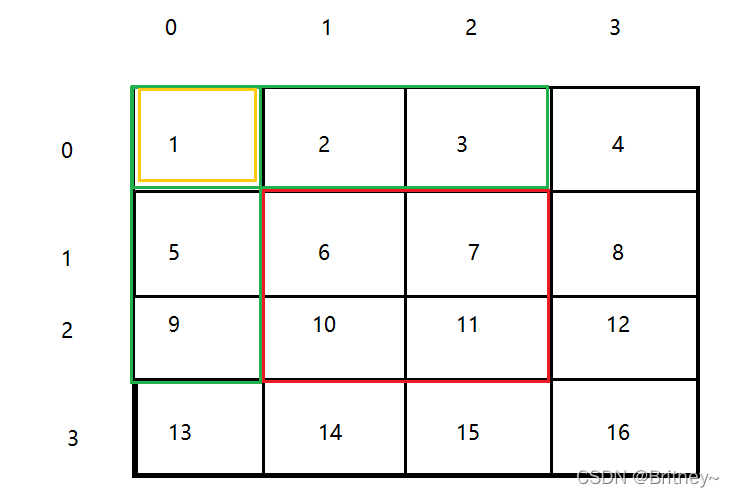
如下图:

如过我们要求(1,1)到 (2,2)的数组和
也就是

也就是上图中红色框中和
当我们要多次询问的话,按普通算法来算的化时间复杂度是O(m*n)
代码如下
#include 这种算法是很低效的,为了提高效率,我们可以先求出二位前缀和数组
sum[i][j]是从(0,0)到(i,j)的和
sum[2][2]
就可以
sum[2][2]=sum[1][2]+sum[2][1]+arr[2][2]-sum[1][1];
结合图还是很好理解的
总结如下:
当 i!=0,j!=0;时
sum[i][j]=sum[i-1][j]+sum[i][j-1]+arr[i][j]-sum[i-1][j-1];
当i==0,j!=0;时
sum[0][j]=sum[0][j-1]+arr[0][j];
当j==0,i!=0时
sum[i][0]=sum[i-1][0]+arr[i][0];
当i== 0, j==0时
sum[0][0]=arr[0][0];
代码如下:
int arr[][4] = { {1 ,2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11,12},
{13,14,15, 16} };
int a = 4, b = 4;
int** sum = (int**)malloc(sizeof(int*) * a);
for (int i = 0; i < a; i++)
{
sum[i] = (int*)malloc(sizeof(int) * b);
for (int j = 0; j < b; j++)
{
if (i == 0 && j == 0)
sum[0][0] = arr[0][0];
else if (i != 0 && j == 0)
sum[i][0] = sum[i - 1][0] + arr[i][0];
else if (i == 0 && j != 0)
sum[0][j] = sum[0][j - 1] + arr[0][j];
else
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + arr[i][j] - sum[i - 1][j - 1];
}
}
当我们有了前缀和数组后,解决最开始的问题就简单多了
如果要求(1,1)到(2,2)的和
sum2=sum[2][2]-sum[2][0]-sum[0][2]+sum[0][0]
总结如下:
(x1,y1),(x2,y2), 前提是 (x1<=x2,y1<=y2)
x1== 0&&y1==0
sum2=sum[x2][y2]
x1!=0&&y1==0
sum2=sum[x2][y2]-sum[x1-1][y2];
x1==0&y1!=0
sum2=sum[x2][y2]-sum[x2][y1-1]
x1!=0&&y1!=0
sum2=sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y2-1];
完整代码:
#include 二维差分
同理还是上面数组
int arr[][4] = { {1 ,2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11,12},
{13,14,15, 16} };
假如我们想要把(1,1)到(2,2)这个区间都加上数字m,用原始的算法也是很慢的,为了加快效率,也是可以用的,也是可以用到差分的,也就是二维差分。
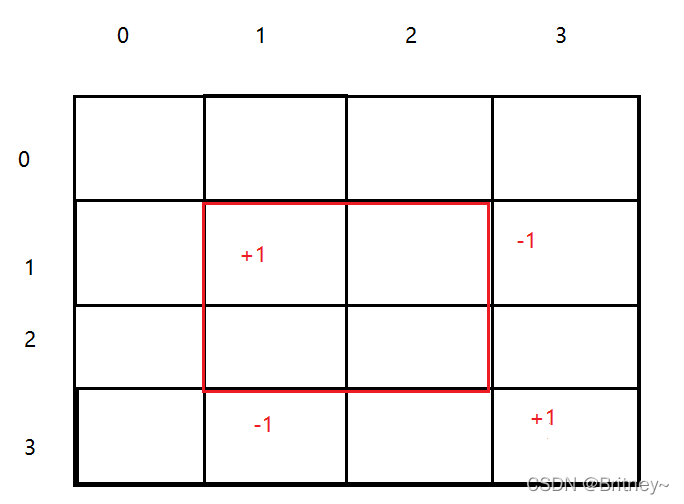
我们只需要对差分数组
sub[1][1]+=m
sub[3][1]-=m
sub[1][3]-=m
sub[3][3]+=m
总结:要在区间(x1,y1)到(x2,y2)都加上m
sub[x1][y1]+=m;
sub[x1][y2+1]-=m;
sub[x2+1][y1]-=m;
sub[x2+1][y2+1]+=m;
代码:
#include 