算法分析与设计——算法问题求解基础
一、实验目的
1.熟悉C/C++语言的集成开发环境;
2.掌握算法的概念;
3.了解问题的求解方法;
4.理解递归思想,学会编写递归。
二、实验原理
- 算法(algorithm)
一个算法是对特定问题求解步骤的一种描述,它是指令的有限序列。算法具有下列 5个特征: 输入(input);输出(output);确定性(definiteness);能行性(effectiveness);有穷性(finiteness)。 - 问题求解过程
理解问题(understand the problem);
设计方案(devise a plan);
实现方案(carry out theplan);
回顾复查(look back)。 - 递归(recursive)
递归定义是一种直接或间接引用自身的定义方法。一个合法的递归定义包括两部分:基础情况(base case)和递归部分。基础情况以直接形式明确列举新事物的若干简单对象,递归部分给出由简单(或较简单)对象定义新对象的条件和方法。
三、实验内容
假币问题
描述:
赛利有12枚银币。其中有11枚真币和1枚假币。假币看起来和真币没有区别,但是重量不同。但赛利不知道假币比真币轻还是重。于是他向朋友借了一架天平。朋友希望赛利称三次就能找出假币并且确定假币是轻是重。例如:如果赛利用天平称两枚硬币,发现天平平衡,说明两枚都是真的。如果赛利用一枚真币与另一枚银币比较,发现它比真币轻或重,说明它是假币。经过精心安排每次的称量,赛利保证在称三次后确定假币。
输入:
第一行有一个数字n,表示有n组测试用例。
对于每组测试用例:
输入有三行,每行表示一次称量的结果。赛利事先将银币标号为A-L。每次称量的结果用三个以空格隔开的字符串表示:天平左边放置的硬币 天平右边放置的硬币 平衡状态。其中平衡状态用``up'', ``down'', 或 ``even''表示, 分别为右端高、右端低和平衡。天平左右的硬币数总是相等的。
输出:
输出哪一个标号的银币是假币,并说明它比真币轻还是重(heavy or light)。
样例输入:
1
ABCD EFGH even
ABCI EFJK up
ABIJ EFGH even
样例输出:
K is the counterfeit coin and it is light.
解题思路 :
-
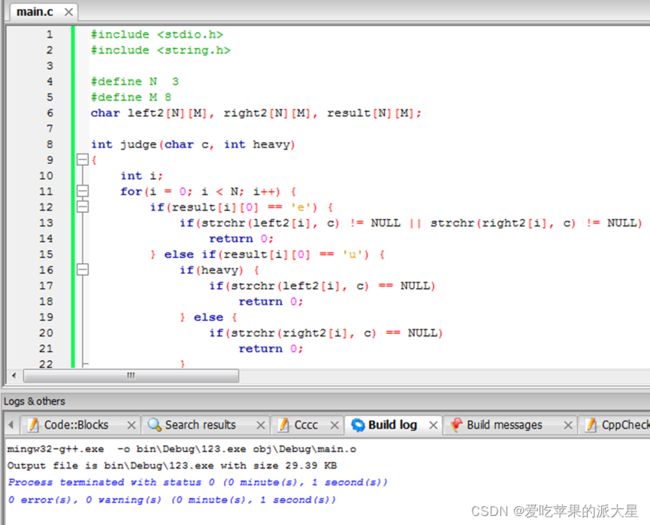
样例输入有3行数据,每行数据有三个字符串,每个字符串长度不超过6个(左右两边最多各放6个银币)。因此,首先设置三个数组来存放输入数据,分别是left[3][7],right[3][7], result[3][7]。因此,
left[0]=ABCD, right[0]=EFGH, result[0]= even
left[1]= ABCI, right[1]= EFJK, result[1]= up
left[2]= ABIJ, right[2]= EFGH, result[2]= even -
银币重量怎么表示?12个银币分别用ABCDEF….L来表示,A是第一个银币, B是第二个银币,… L是第12个银币,假设用数组status来存放银币重量:
A ------> status[0]
B ------> status[1]
C ------> status[2]
D ------> status[3]
…
L ------> status[12]先给12个银币的重量赋值
for(i=0;i<12;i++) status[i]=0
每个金币有两种情况,所以采用枚举法,变量分别是每个金币的编号x和轻重2种情况。在所有可能的24种猜测中,枚举每个金币及其轻重,当满足所有条件时为假设成立。
for(i=0;i<12;i++)
假设轻银币重量为-1 status[i]=-1;if (isBalance()) break;
假设重银币重量为1; status[i]=1; if (isBalance()) break;
假设正常银币重量为0 status[i]=0;
- ABCD EFGH even:天平左边放ABCD四个银币,右边放EFGH四个银币,状态是even;即left=A银币的重量+ B银币的重量+ C银币的重量+ D银币的重量,right=E银币的重量+ F银币的重量+ G银币的重量+ H银币的重量。将银币重量带入,判断是否满足条件。如果满足输出true,否则输出false。
bool isBalance()
{
for(i=0;i<3;i++)
{
leftw=rightw=0;
for(j=0;j<6 && left[i][j]!=0;j++)
{
leftw+=status[left[i][j]-‘A’];
rightw+=status[right[i][j]-‘A’];
}
If (leftw== rightw && result[i][0]!=’e’)
return false;
If (leftw> rightw && result[i][0]!=’u’)
return false;
If (leftw< rightw && result[i][0]!=’d’)
return false;
}
return true;
}
问题分析:
根据给定的条件,标记银币重量是否正确的做法是难以得到需要的答案的。
暴力法是必要的。12枚银币分别是A-L,那么A-L都有可能重了或轻了,共有24种情况,分别试一下就知道了。
代码:
#include 4148:生理周期
描述:
人生来就有三个生理周期,分别为体力周期、感情周期和智力周期,它们的周期长度分别为23天、28天和33天。每一个周期中有一天是高峰。在高峰这天,人会在相应的方面表现出色。例如,在智力周期的高峰,人会思维敏捷,注意力容易高度集中。因为三个周期的长度不同,所以通常三个周期的高峰不会落在同一天。对于每个人,想知道何时三个高峰落在同一天。对于每个周期,会给出从当前年份的第一天开始,到出现高峰的天数(不一定是第一次高峰出现的时间)。给定一个从当年第一天开始的天数,你的任务是输出从给定时间开始(不包括给定时间),下一次三个高峰落在同一天的时间(距给定时间的天数)。例如:给定时间为10,下次出现三个高峰同一天的时间是12,则输出2(注意这里不是3)。
输入:
输入包含多组数据,每一组数据由四个整数组成,数据以-1 -1 -1 -1 结束。对于四个整数p, e, i和d,p, e, i分别表示体力、情感和智力高峰出现的时间(时间从当年的第一天开始计算)。d是给定的时间,可能小于p, e或i。所有给定时间是非负的并且小于或等于365,所求的时间小于或等于21252。
输出:
从给定时间起,下一次三个高峰同一天的时间(距离给定时间的天数)。
样例输入:
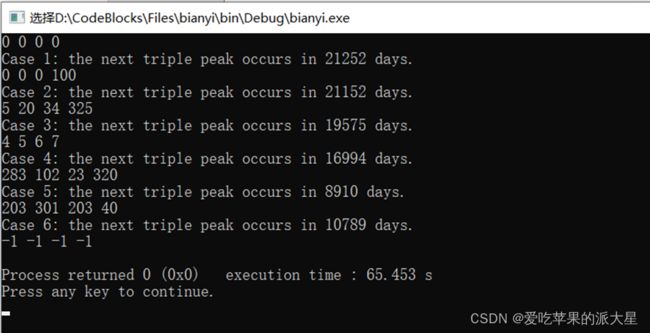
0 0 0 0
0 0 0 100
5 20 34 325
4 5 6 7
283 102 23 320
203 301 203 40
-1 -1 -1 -1
样例输出:
Case 1: the next triple peak occurs in 21252 days.
Case 2: the next triple peak occurs in 21152 days.
Case 3: the next triple peak occurs in 19575 days.
Case 4: the next triple peak occurs in 16994 days.
Case 5: the next triple peak occurs in 8910 days.
Case 6: the next triple peak occurs in 10789 days.
解题思路:
这里可以这样理解,如果第n天满足条件,那么肯定三个周期经历了n1,n2,n3个轮回,加上初始化的天数,都等于n,也就是说,假设第1024天符合条件,那么对于例子中的第3行,必定有:1024=23n1+5,1024=28n2+20,1024=33*n3+34,所以,只要判断,这一天是不是符合条件:(d-5)%23 == 0 && (d-20)%28 == 0 && (d-34)%33 == 0,枚举即可。
代码:
#include