Go-Python-Java-C-LeetCode高分解法-第十一周合集

前言

本题解Go语言部分基于 LeetCode-Go
其他部分基于本人实践学习
个人题解GitHub连接：LeetCode-Go-Python-Java-C
欢迎订阅CSDN专栏，每日一题，和博主一起进步
LeetCode专栏
我搜集到了50道精选题，适合速成概览大部分常用算法
突破算法迷宫：精选50道-算法刷题指南

71. Simplify Path

题目

Given an absolute path for a file (Unix-style), simplify it. Or in other words, convert it to the canonical path.

In a UNIX-style file system, a period . refers to the current directory. Furthermore, a double period … moves the directory up a level. For more information, see: Absolute path vs relative path in Linux/Unix

Note that the returned canonical path must always begin with a slash /, and there must be only a single slash / between two directory names. The last directory name (if it exists) must not end with a trailing /. Also, the canonical path must be the shortest string representing the absolute path.

Example 1:

Input: "/home/"
Output: "/home"
Explanation: Note that there is no trailing slash after the last directory name.

Example 2:

Input: "/../"
Output: "/"
Explanation: Going one level up from the root directory is a no-op, as the root level is the highest level you can go.

Example 3:

Input: "/home//foo/"
Output: "/home/foo"
Explanation: In the canonical path, multiple consecutive slashes are replaced by a single one.

Example 4:

Input: "/a/./b/../../c/"
Output: "/c"

Example 5:

Input: "/a/../../b/../c//.//"
Output: "/c"

Example 6:

Input: "/a//bc/d//././/.."
Output: "/a/b/c"

题目大意

给出一个 Unix 的文件路径，要求简化这个路径。这道题也是考察栈的题目。

解题思路

这道题笔者提交了好多次才通过，并不是题目难，而是边界条件很多，没考虑全一种情况就会出错。有哪些边界情况就看笔者的 test 文件吧。
当处理这个问题时，我们需要使用一个栈数据结构来辅助，以下是各个版本的解题思路：

C++ 版本

在C++版本中，我们使用了STL库中的stack容器来实现栈。算法思路如下：

1. 首先，我们将输入的路径按照斜杠/分割成目录列表。
2. 创建一个空的栈，遍历目录列表中的每个目录名。
3. 如果遇到普通目录名（不为空且不为.），将其入栈。
4. 如果遇到..，表示返回上一级目录，出栈一个目录。
5. 遍历完所有目录后，栈中的元素即为简化后的路径。
6. 最后，将栈中的元素连接起来，形成简化后的路径。

Java 版本

在Java版本中，我们使用Stack类来实现栈。算法思路如下：

1. 首先，将输入的路径按照斜杠/分割成目录列表。
2. 创建一个空的栈，遍历目录列表中的每个目录名。
3. 如果遇到普通目录名（不为空且不为.），将其入栈。
4. 如果遇到..，表示返回上一级目录，出栈一个目录。
5. 遍历完所有目录后，栈中的元素即为简化后的路径。
6. 最后，将栈中的元素连接起来，形成简化后的路径。

Python 版本

在Python版本中，我们使用列表（list）模拟栈的操作。算法思路如下：

1. 首先，将输入的路径按照斜杠/分割成目录列表。
2. 创建一个空的列表，遍历目录列表中的每个目录名。
3. 如果遇到普通目录名（不为空且不为.），将其加入列表。
4. 如果遇到..，表示返回上一级目录，出栈一个目录。
5. 遍历完所有目录后，列表中的元素即为简化后的路径。
6. 最后，将列表中的元素连接起来，形成简化后的路径。

Go 版本

在Go版本中，我们使用了内置的stack库实现栈。算法思路如下：

1. 首先，将输入的路径按照斜杠/分割成目录列表。
2. 创建一个空的栈，遍历目录列表中的每个目录名。
3. 如果遇到普通目录名（不为空且不为.），将其入栈。
4. 如果遇到..，表示返回上一级目录，出栈一个目录。
5. 遍历完所有目录后，栈中的元素即为简化后的路径。
6. 最后，将栈中的元素连接起来，形成简化后的路径。

以上就是各个版本的解题思路，它们的核心思想都是使用栈来模拟文件系统的路径，并根据.和..的出现进行相应的入栈和出栈操作，最终得到简化后的路径。希望这些解题思路能够帮助你更好地理解问题的解决方法！

代码

Go

class Solution {
public:
    string simplifyPath(string path) {
        // 创建一个空栈
        stack st;
        
        // 使用 "/" 字符来分割输入的路径字符串
        stringstream ss(path);
        string token;
        
        while (getline(ss, token, '/')) {
            if (token == "..") {
                // 如果遇到 ".." 表示要返回上一级目录
                if (!st.empty()) {
                    st.pop();
                }
            } else if (!token.empty() && token != ".") {
                // 如果不是空字符串或者当前目录 ".", 则入栈（表示进入下一级目录）
                st.push(token);
            }
        }
        
        // 使用 "/" 连接栈内的元素，形成简化后的路径
        string result = "";
        while (!st.empty()) {
            result = "/" + st.top() + result;
            st.pop();
        }
        
        return result.empty() ? "/" : result;
    }
};

Python

class Solution:
    def simplifyPath(self, path: str) -> str:
        # 将输入路径按照斜杠分割成目录列表
        path_list = path.split("/")
        
        # 初始化一个空栈，用于存储简化后的路径
        stack = []

        # 遍历路径中的每个目录
        for item in path_list:
            # 如果当前目录是 ".."，则从栈中返回上一级目录（出栈）
            if item == "..":
                if stack:
                    stack.pop()
            # 如果当前目录不为空且不是 "."，则将其压入栈中
            elif item and item != '.':
                stack.append(item)

        # 通过连接栈中的目录，构建简化后的路径
        return "/" + "/".join(stack)

Java

public class Solution {
    public String simplifyPath(String path) {
        // 如果输入的路径为空，则直接返回根目录 "/"
        if (path.length() == 0) return "/";

        // 初始化一个字符数组，用于存储简化后的路径
        char[] arr = new char[path.length()];
        arr[0] = '/'; // 将第一个字符设为根目录
        int len = 1; // 初始化简化路径的长度

        // 将输入路径字符串转换为字符数组
        char[] chars = path.toCharArray();
        int s = 0; // 用于遍历输入路径字符的索引

        // 遍历输入路径的字符
        while (s < chars.length) {
            // 跳过单个点（"."）
            if (chars[s] == '.' && (s == chars.length - 1 || chars[s + 1] == '/')) {
                s++;
                continue;
            }
            // 处理双点（".."）
            if (chars[s] == '.' && s + 1 < chars.length && chars[s + 1] == '.'
                    && (s + 1 == chars.length - 1 || chars[s + 2] == '/')) {
                // 返回到上一级目录（向上移动）
                while (len > 0 && arr[len - 1] != '/') len--;
                if (len > 1 && arr[len - 1] == '/') len--;
            } else if (chars[s] != '/') {
                // 如果当前字符不是斜杠（"/"）
                // 如果最后一个字符不是斜杠，则在简化路径中添加一个斜杠
                if (arr[len - 1] != '/') {
                    arr[len++] = '/';
                }
                // 将字符复制到简化路径，直到下一个斜杠
                while (s < chars.length && chars[s] != '/') {
                    arr[len++] = chars[s++];
                }
            }
            s++; // 移动到输入路径的下一个字符
        }

        // 从简化路径字符数组中创建新字符串
        return new String(arr, 0, len);
    }
}

Cpp

#include 
#include 
#include 

class Solution {
public:
    std::string simplifyPath(std::string path) {
        // 如果输入的路径为空，则直接返回根目录 "/"
        if (path.empty()) {
            return "/";
        }

        // 将输入路径按斜杠分割成目录列表
        std::vector dirs;
        std::istringstream iss(path);
        std::string dir;

        // 用于存储简化后的路径的栈
        std::vector stack;

        // 将目录分割后存入目录列表
        while (getline(iss, dir, '/')) {
            dirs.push_back(dir);
        }

        // 遍历目录列表
        for (const auto& dir : dirs) {
            // 跳过空目录和单个点（"."）
            if (dir.empty() || dir == ".") {
                continue;
            }
            // 处理双点（".."）
            else if (dir == "..") {
                // 如果栈不为空，则返回上一级目录（出栈）
                if (!stack.empty()) {
                    stack.pop_back();
                }
            } else {
                // 其他目录名入栈
                stack.push_back(dir);
            }
        }

        // 构建简化后的路径
        std::string simplified_path = "/";
        for (const auto& dir : stack) {
            simplified_path += dir + "/";
        }

        // 如果简化后的路径为空，返回根目录 "/"
        return simplified_path == "/" ? simplified_path : simplified_path.substr(0, simplified_path.size() - 1);
    }
};

 

当解决LeetCode上的算法问题时，无论使用哪种编程语言，都需要掌握以下基础知识：

1. 字符串操作

• C++/Java/Python: 熟练使用字符串的拼接、切片、分割等操作。

  std::string result = "/";
  result += dir;
  

  String result = "/";
  result += dir;
  

  result = result + "/" + dir
  

2. 数组或列表操作

• C++: 使用STL库中的vector容器。

  std::vector<std::string> stack;
  stack.push_back(dir);
  

• Java: 使用ArrayList或数组。

  ArrayList<String> stack = new ArrayList<>();
  stack.add(dir);
  

• Python: 使用列表（list）。

  stack.append(dir)
  

3. 栈（Stack）数据结构

• C++: 使用STL库中的stack容器。

  std::stack<std::string> st;
  st.push(dir);
  

• Java: 使用Stack类或者LinkedList实现栈。

  Stack<String> stack = new Stack<>();
  stack.push(dir);
  

• Python: 利用列表模拟栈的操作。

  stack.append(dir)
  

4. 流处理（仅针对C++和Java）

• C++: 使用istringstream来分割字符串。

  std::istringstream iss(path);
  std::string dir;
  while (getline(iss, dir, '/')) {
      // 处理目录
  }
  

• Java: 使用StringTokenizer或者split方法来分割字符串。

  StringTokenizer tokenizer = new StringTokenizer(path, "/");
  while (tokenizer.hasMoreTokens()) {
      String dir = tokenizer.nextToken();
      // 处理目录
  }
  

5. 条件判断和循环

• C++/Java/Python: 掌握if、else if、else条件判断语句和while、for循环语句的使用。

6. 面向对象编程（仅针对Java）

• Java: 如果使用Java，需要了解类、对象、方法等面向对象编程的基本概念，以及如何定义和使用类。

以上是解决LeetCode算法问题时需要掌握的基础知识。对于不同编程语言，语法细节和一些特有的数据结构可能有所不同，但以上提到的基础知识是通用的。希望这些信息对你有所帮助，如果有任何疑问，请随时向我提问！

72. Edit-Distance

题目

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

Insert a character
Delete a character
Replace a character

Example 1:

Input: word1 = “horse”, word2 = “ros”
Output: 3
Explanation:
horse -> rorse (replace ‘h’ with ‘r’)
rorse -> rose (remove ‘r’)
rose -> ros (remove ‘e’)
Example 2:

Input: word1 = “intention”, word2 = “execution”
Output: 5
Explanation:
intention -> inention (remove ‘t’)
inention -> enention (replace ‘i’ with ‘e’)
enention -> exention (replace ‘n’ with ‘x’)
exention -> exection (replace ‘n’ with ‘c’)
exection -> execution (insert ‘u’)

Constraints:

0 <= word1.length, word2.length <= 500
word1 and word2 consist of lowercase English letters.

题目大意

给你两个单词word1 和word2， 请返回将word1转换成word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

解题思路

以下是每个版本的解题思路的详细介绍：

Go 版本解题思路：

1. 初始化：创建一个二维切片 f，其中 f[i][j] 表示将字符串 s 的前 i 个字符转换为字符串 t 的前 j 个字符所需的最小操作数。初始化第一行和第一列，表示从空字符串到各个字符串的编辑距离。

2. 动态规划：遍历字符串 s 和 t 的每个字符，逐个比较它们。如果字符相同，f[i][j] 等于 f[i-1][j-1]；否则，f[i][j] 等于 f[i-1][j]（删除操作）、f[i][j-1]（插入操作）和 f[i-1][j-1]（替换操作）中的最小值加一。

3. 返回结果：最后返回 f[n][m]，其中 n 和 m 是字符串 s 和 t 的长度。

Python 版本解题思路：

1. 初始化：创建一个二维数组 f，其中 f[i][j] 表示将字符串 word1 的前 i 个字符转换为字符串 word2 的前 j 个字符所需的最小操作数。初始化第一行和第一列，表示从空字符串到各个字符串的编辑距离。

2. 动态规划：遍历字符串 word1 和 word2 的每个字符，逐个比较它们。如果字符相同，f[i][j] 等于 f[i-1][j-1]；否则，f[i][j] 等于 f[i-1][j]（删除操作）、f[i][j-1]（插入操作）和 f[i-1][j-1]（替换操作）中的最小值加一。

3. 返回结果：最后返回 f[n][m]，其中 n 和 m 是字符串 word1 和 word2 的长度。

Java 版本解题思路：

1. 初始化：将输入的字符串 word1 和 word2 转换为字符数组 ch1 和 ch2。创建两个整数数组 lastRow 和 thisRow，它们用于存储编辑距离计算中的临时结果。

2. 动态规划：遍历字符数组 ch1 和 ch2，逐个比较字符。如果字符相同，thisRow[j] 等于 lastRow[j-1]；否则，thisRow[j] 等于 lastRow[j]（删除操作）、thisRow[j-1]（插入操作）和 lastRow[j-1]（替换操作）中的最小值加一。

3. 交替行：在每次计算后，交换 lastRow 和 thisRow，以便下一次迭代使用。

4. 返回结果：最后返回 lastRow[ch2.length]，即从 word1 到 word2 的最小编辑距离。

C++ 版本解题思路：

1. 初始化：获取输入字符串 word1 和 word2 的长度，创建一个二维数组 dp 用于存储编辑距离计算中的临时结果。

2. 动态规划：遍历字符串 word1 和 word2 的每个字符，逐个比较它们。如果字符相同，dp[i][j] 等于 dp[i-1][j-1]；否则，dp[i][j] 等于 dp[i-1][j]（删除操作）、dp[i][j-1]（插入操作）和 dp[i-1][j-1]（替换操作）中的最小值加一。

3. 返回结果：最后返回 dp[n][m]，其中 n 和 m 是字符串 word1 和 word2 的长度。

在每个版本中，动态规划是主要的解题思路，其中二维数组用于存储中间结果，逐步构建最小编辑距离。最终的目标是得到 f[n][m] 或 dp[n][m]，即从一个字符串到另一个字符串的最小编辑距离。

代码

Go

func minDistance(s, t string) int {
    n, m := len(s), len(t)   // 获取字符串s和t的长度
    f := make([][]int, n+1)  // 创建一个(n+1) x (m+1)的二维切片f，用于存储编辑距离计算中的临时结果
    for i := range f {       // 初始化f二维切片
        f[i] = make([]int, m+1)
    }
    for j := 1; j <= m; j++ { // 初始化f的第一行，表示从空字符串s到t的编辑距离
        f[0][j] = j
    }
    for i, x := range s {     // 遍历字符串s的字符
        f[i+1][0] = i + 1     // 初始化f的第一列，表示从空字符串t到s的编辑距离
        for j, y := range t { // 遍历字符串t的字符
            if x == y {       // 如果当前字符相同
                f[i+1][j+1] = f[i][j] // 编辑距离不变
            } else {
                f[i+1][j+1] = min(min(f[i][j+1], f[i+1][j]), f[i][j]) + 1
                // 否则，计算替换、插入和删除操作中的最小编辑距离
            }
        }
    }
    return f[n][m] // 返回s到t的最小编辑距离
}

func min(a, b int) int {
    if b < a {
        return b
    }
    return a
}

Python

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        n, m = len(word1), len(word2)
        # 创建一个(n+1) x (m+1)的二维数组，用于存储编辑距离计算中的临时结果
        f = [[0] * (m + 1) for _ in range(n + 1)]

        # 初始化第一行和第一列
        for i in range(n + 1):
            f[i][0] = i
        for j in range(m + 1):
            f[0][j] = j

        # 动态规划计算编辑距离
        for i in range(1, n + 1):
            for j in range(1, m + 1):
                if word1[i - 1] == word2[j - 1]:
                    f[i][j] = f[i - 1][j - 1]
                else:
                    f[i][j] = min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1

        return f[n][m]

    def min(self, a, b, c):
        return min(a, min(b, c))

Java

class Solution {
    public int minDistance(String word1, String word2) {
        char[] ch1 = word1.toCharArray(); // 将字符串 word1 转换为字符数组 ch1
        char[] ch2 = word2.toCharArray(); // 将字符串 word2 转换为字符数组 ch2
        int[] lastRow = new int[ch2.length + 1]; // 上一行的编辑距离数组
        int[] thisRow = new int[ch2.length + 1]; // 当前行的编辑距离数组
        int[] temp; // 用于交换 lastRow 和 thisRow 的临时数组
        int tempMin; // 用于暂存最小编辑距离的临时变量

        // 初始化上一行，表示从空字符串 word1 到 word2 的编辑距离
        for (int j = 1; j <= ch2.length; j++) {
            lastRow[j] = lastRow[j - 1] + 1;
        }

        // 遍历字符串 word1 的字符
        for (int i = 1; i <= ch1.length; i++) {
            thisRow[0] = lastRow[0] + 1; // 初始化当前行的第一个元素

            // 遍历字符串 word2 的字符
            for (int j = 1; j <= ch2.length; j++) {
                if (ch1[i - 1] == ch2[j - 1]) {
                    thisRow[j] = lastRow[j - 1]; // 如果字符相同，编辑距离不变
                } else {
                    // 如果字符不同，计算替换、插入和删除操作中的最小编辑距离
                    tempMin = Math.min(lastRow[j], Math.min(thisRow[j - 1], lastRow[j - 1]));
                    thisRow[j] = tempMin + 1;
                }
            }

            // 交换 lastRow 和 thisRow
            temp = lastRow;
            lastRow = thisRow;
            thisRow = temp;
        }

        return lastRow[ch2.length]; // 返回最终的编辑距离
    }
}

Cpp

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.length();
        int m = word2.length();

        // 如果其中一个字符串为空，返回另一个字符串的长度，这是初始状态
        if (n == 0 || m == 0) return max(n, m);

        int dp[n + 1][m + 1];
        memset(dp, 0, sizeof(dp));

        // 初始化第一行和第一列
        for (int i = 0; i < n + 1; i++) {
            dp[i][0] = i;
        }
        for (int i = 0; i < m + 1; i++) {
            dp[0][i] = i;
        }

        // 动态规划计算编辑距离
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < m + 1; j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    // 如果当前字符相同，不需要执行替换操作
                    dp[i][j] = min(dp[i - 1][j] + 1, min(dp[i][j - 1] + 1, dp[i - 1][j - 1]));
                } else {
                    // 如果当前字符不同，执行替换操作并加1
                    dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
                }
            }
        }
        return dp[n][m]; // 返回编辑距离
    }
};

 

以下是每个版本的所需基础知识的详细介绍：

Go 版本：

1. 变量和数据类型：了解 Go 中的基本数据类型（整数、字符串、字符等），以及如何声明和使用变量。

2. 切片和数组：理解 Go 中的切片和数组，它们在字符串处理中经常用到。

3. 循环和条件语句：掌握 Go 中的循环和条件语句，用于控制程序流程。

4. 函数：了解如何定义和调用函数，以及如何传递参数和返回值。

5. 切片操作：学习如何对切片进行操作，例如添加和删除元素。

6. 动态规划：理解动态规划的基本思想，包括如何使用二维数组来存储中间结果以解决问题。

Python 版本：

1. 变量和数据类型：了解 Python 中的数据类型（整数、字符串、列表等），以及如何声明和使用变量。

2. 列表：学会使用列表，因为它们在字符串处理和动态规划中经常用到。

3. 循环和条件语句：掌握 Python 中的循环和条件语句，用于控制程序流程。

4. 函数：了解如何定义和调用函数，以及如何传递参数和返回值。

5. 动态规划：理解动态规划的基本思想，包括如何使用二维数组来存储中间结果以解决问题。

Java 版本：

1. 类和对象：Java 是面向对象的编程语言，所以需要了解类和对象的概念，以及如何创建对象。

2. 字符数组：了解字符数组的使用，因为字符串操作通常涉及字符数组。

3. 循环和条件语句：掌握 Java 中的循环和条件语句，用于控制程序流程。

4. 方法：了解如何定义和调用方法，以及如何传递参数和返回值。

5. 动态规划：理解动态规划的基本思想，包括如何使用二维数组来存储中间结果以解决问题。

C++ 版本：

1. 变量和数据类型：了解 C++ 中的数据类型（整数、字符串、数组等），以及如何声明和使用变量。

2. 数组：学会使用数组，因为它们在字符串处理和动态规划中经常用到。

3. 循环和条件语句：掌握 C++ 中的循环和条件语句，用于控制程序流程。

4. 函数：了解如何定义和调用函数，以及如何传递参数和返回值。

5. 动态规划：理解动态规划的基本思想，包括如何使用二维数组来存储中间结果以解决问题。

在每种版本中，你还需要了解动态规划的核心思想，即如何将一个大问题拆分为子问题，以及如何使用中间结果来优化解决方案。这种问题解决方法在编程中非常常见，因此对动态规划的理解至关重要。

73. Set Matrix Zeroes

题目

Given an *m* x *n* matrix. If an element is 0, set its entire row and column to 0. Do it in-place.

Follow up:

• A straight forward solution using O(mn) space is probably a bad idea.
• A simple improvement uses O(m + n) space, but still not the best solution.
• Could you devise a constant space solution?

Example 1:

Input: matrix = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[1,0,1],[0,0,0],[1,0,1]]

Example 2:

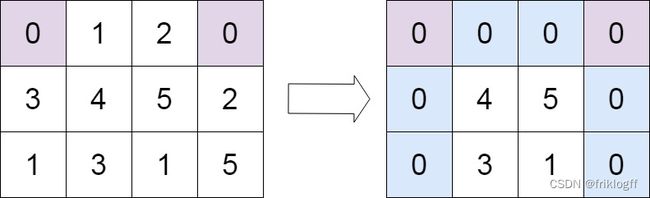
Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]]

Constraints:

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• 2^31 <= matrix[i][j] <= 2^31 - 1

题目大意

给定一个 m x n 的矩阵，如果一个元素为 0，则将其所在行和列的所有元素都设为 0。请使用原地算法。

解题思路

• 此题考查对程序的控制能力，无算法思想。题目要求采用原地的算法，所有修改即在原二维数组上进行。在二维数组中有 2 个特殊位置，一个是第一行，一个是第一列。它们的特殊性在于，它们之间只要有一个 0，它们都会变为全 0 。先用 2 个变量记录这一行和这一列中是否有 0，防止之后的修改覆盖了这 2 个地方。然后除去这一行和这一列以外的部分判断是否有 0，如果有 0，将它们所在的行第一个元素标记为 0，所在列的第一个元素标记为 0 。最后通过标记，将对应的行列置 0 即可。
  以下是每个版本的解题思路的详细说明：

Go版本：

1. 首先检查矩阵是否为空，如果为空则直接返回。
2. 初始化两个布尔变量 isFirstRowExistZero 和 isFirstColExistZero，用于标记第一行和第一列是否包含0。
3. 遍历矩阵，检查第一列是否包含0，如果包含0，将 isFirstColExistZero 设为 true。
4. 同样地，检查第一行是否包含0，如果包含0，将 isFirstRowExistZero 设为 true。
5. 接下来，遍历矩阵的其余部分（除了第一行和第一列），如果某个元素为0，将对应的第一行和第一列的元素设置为0。
6. 再次遍历矩阵的其余部分，根据第一行和第一列的标记，将对应的行和列设置为0。
7. 最后，如果 isFirstRowExistZero 为 true，将整个第一行设置为0；如果 isFirstColExistZero 为 true，将整个第一列设置为0。

Python版本：

1. 检查矩阵是否为空，如果为空则直接返回。
2. 初始化两个布尔变量 first_row_has_zero 和 first_col_has_zero，用于标记第一行和第一列是否包含0。
3. 遍历矩阵，检查第一列是否包含0，如果包含0，将 first_col_has_zero 设为 true。
4. 同样地，检查第一行是否包含0，如果包含0，将 first_row_has_zero 设为 true。
5. 遍历矩阵的其余部分（除了第一行和第一列），如果某个元素为0，将对应的第一行和第一列的元素设置为0。
6. 再次遍历矩阵的其余部分，根据第一行和第一列的标记，将对应的行和列设置为0。
7. 最后，如果 first_row_has_zero 为 true，将整个第一行设置为0；如果 first_col_has_zero 为 true，将整个第一列设置为0。

Java版本：

1. 获取矩阵的行数和列数。
2. 创建两个布尔数组 rowboolean 和 colboolean，分别用于标记行和列中是否存在0元素，并初始化为全false。
3. 遍历矩阵的每个元素，如果某个元素为0，将对应的行和列在 rowboolean 和 colboolean 中标记为true。
4. 再次遍历矩阵，根据 rowboolean 和 colboolean 的标记，将对应的行和列置零。

C++版本：

1. 获取矩阵的行数和列数。
2. 创建两个布尔变量 firstRowZero 和 firstColZero，用于标记第一行和第一列是否包含0。
3. 遍历矩阵，检查第一列是否包含0，如果包含0，将 firstColZero 设为 true。
4. 同样地，检查第一行是否包含0，如果包含0，将 firstRowZero 设为 true。
5. 使用第一行和第一列来标记需要置零的行和列。
6. 遍历矩阵的其余部分，如果某个元素为0，将对应的第一行和第一列的元素设置为0。
7. 再次遍历矩阵的其余部分，根据第一行和第一列的标记，将对应的行和列设置为0。
8. 最后，如果 firstRowZero 为 true，将整个第一行设置为0；如果 firstColZero 为 true，将整个第一列设置为0。

这些解题思路的共同点是使用额外的标记来记录哪些行和列需要设置为0，并然后按照这些标记来进行相应的操作，以满足题目要求。

代码

Go

func setZeroes(matrix [][]int) {
	// 检查矩阵是否为空
	if len(matrix) == 0 || len(matrix[0]) == 0 {
		return
	}

	// 初始化两个标志变量，用于判断第一行和第一列是否需要被置零
	isFirstRowExistZero, isFirstColExistZero := false, false

	// 检查第一列是否存在零元素
	for i := 0; i < len(matrix); i++ {
		if matrix[i][0] == 0 {
			isFirstColExistZero = true
			break
		}
	}

	// 检查第一行是否存在零元素
	for j := 0; j < len(matrix[0]); j++ {
		if matrix[0][j] == 0 {
			isFirstRowExistZero = true
			break
		}
	}

	// 遍历矩阵，如果元素为零，则将对应的第一行和第一列的元素置零
	for i := 1; i < len(matrix); i++ {
		for j := 1; j < len(matrix[0]); j++ {
			if matrix[i][j] == 0 {
				matrix[i][0] = 0
				matrix[0][j] = 0
			}
		}
	}

	// 处理除第一行以及第一列以外的行，将包含零元素的行全部置零
	for i := 1; i < len(matrix); i++ {
		if matrix[i][0] == 0 {
			for j := 1; j < len(matrix[0]); j++ {
				matrix[i][j] = 0
			}
		}
	}

	// 处理除第一行以及第一列以外的列，将包含零元素的列全部置零
	for j := 1; j < len(matrix[0]); j++ {
		if matrix[0][j] == 0 {
			for i := 1; i < len(matrix); i++ {
				matrix[i][j] = 0
			}
		}
	}

	// 如果第一行存在零元素，则将整个第一行置零
	if isFirstRowExistZero {
		for j := 0; j < len(matrix[0]); j++ {
			matrix[0][j] = 0
		}
	}

	// 如果第一列存在零元素，则将整个第一列置零
	if isFirstColExistZero {
		for i := 0; i < len(matrix); i++ {
			matrix[i][0] = 0
		}
	}
}

Python

class Solution:
    def setZeroes(self, matrix):
        """
        Do not return anything, modify matrix in-place instead.
        """
        if not matrix or not matrix[0]:
            return

        # 初始化标志变量
        first_row_has_zero = any(matrix[0][j] == 0 for j in range(len(matrix[0])))
…        # 处理第一行和第一列
        if first_row_has_zero:
            for j in range(len(matrix[0])):
                matrix[0][j] = 0
        if first_col_has_zero:
            for i in range(len(matrix)):
                matrix[i][0] = 0

Java

class Solution {
    public void setZeroes(int[][] matrix) {
        int row = matrix.length;//行数
		int col = matrix[0].length;//列数
		boolean[] rowboolean = new boolean[row];//行数组，初始false
		boolean[] colboolean = new boolean[col];//列数组，初始false
		for (int i = 0; i < row; i++) {
			for (int j = 0; j < col; j++) {
				if(matrix[i][j] == 0){
					rowboolean[i] = true;
…		}
    }
}

Cpp

class Solution {
public:
    void setZeroes(vector>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        bool firstRowZero = false;
        bool firstColZero = false;

        // 检查第一行和第一列是否包含零
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                firstColZero = true;
                break;
            }
        }
        for (int j = 0; j < n; j++) {
            if (matrix[0][j] == 0) {
                firstRowZero = true;
                break;
            }
        }

        // 使用第一行和第一列来标记需要置零的行和列
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }

        // 根据标记，将对应的行和列置零
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }

        // 处理第一行和第一列
        if (firstColZero) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
        if (firstRowZero) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }
    }
};

当使用不同编程语言编写代码时，为理解和修改代码，需要了解以下基础知识：

Go版本：

• Go是一种静态编程语言，它具有强类型系统。
• 在Go中，你需要了解如何声明和使用变量、数组和切片（slices）。
• 了解循环和条件语句，例如for和if。
• 理解二维切片（2D slices）和如何通过索引访问元素。
• 函数的定义和调用方式，以及如何处理函数参数和返回值。
• 在Go中，数组和切片的长度可以使用len()函数获得。
• 使用布尔（boolean）类型来标记特定条件的存在与否。

Python版本：

• Python是一种动态脚本语言，具有弱类型系统。
• 了解Python的基本数据结构，如列表（lists）和嵌套列表。
• 掌握条件语句（如if）和循环结构（如for）的用法。
• 理解如何定义和调用函数，以及如何处理函数参数和返回值。
• 在Python中，你可以使用列表和嵌套列表来表示矩阵。
• 使用布尔类型来标记特定条件的存在与否，如if element == 0。

Java版本：

• Java是一种强类型编程语言，具有静态类型检查。
• 了解Java的类和对象，以及如何创建和操作二维数组。
• 掌握条件语句（如if）和循环结构（如for）的语法。
• 熟悉如何定义和调用方法（函数）。
• Java中的数组是定长的，需要提前指定大小。
• 使用布尔数组来标记特定条件的存在与否。

C++版本：

• C++是一种强类型编程语言，具有静态类型检查。
• 了解C++的类和对象，以及如何创建和操作二维数组。
• 掌握条件语句（如if）和循环结构（如for）的语法。
• 理解如何定义和调用函数，以及如何处理函数参数和返回值。
• C++中的数组是定长的，需要提前指定大小。
• 使用布尔数组来标记特定条件的存在与否。

无论使用哪种编程语言，理解基本的控制结构、数组/列表、条件语句和循环结构都是解决问题的关键。此外，了解如何在特定编程语言中声明变量、定义函数以及操作数据结构也是重要的基础知识。

74. Search a 2D Matrix

题目

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3
Output: true

Example 2:

Input:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 13
Output: false

题目大意

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

• 每行中的整数从左到右按升序排列。
• 每行的第一个整数大于前一行的最后一个整数。

解题思路

• 给出一个二维矩阵，矩阵的特点是随着矩阵的下标增大而增大。要求设计一个算法能在这个矩阵中高效的找到一个数，如果找到就输出 true，找不到就输出 false。
• 虽然是一个二维矩阵，但是由于它特殊的有序性，所以完全可以按照下标把它看成一个一维矩阵，只不过需要行列坐标转换。最后利用二分搜索直接搜索即可。
  以下是每个版本的解题思路的详细介绍：

Go 版本解题思路

1. 首先，检查输入的矩阵是否为空（长度为0）。如果矩阵为空，直接返回 false，因为无法在空矩阵中查找目标值。

2. 获取矩阵的列数（m），并初始化两个指针 low 和 high。low 初始化为0，high 初始化为矩阵中元素总数减1，表示搜索范围的开始和结束。

3. 进入一个循环，条件是 low 小于等于 high。这个循环是二分查找的核心部分。

4. 在循环中，首先计算中间索引 mid，以将搜索范围分成两半。这是通过 low + (high - low) >> 1 来实现的，使用位运算右移来取代除以2，以提高效率。

5. 然后，使用整数除法和取模运算，将 mid 转换为矩阵中的行和列索引，即 mid/m 和 mid%m。

6. 比较矩阵中索引为 mid/m 行，mid%m 列的元素与目标值 target。如果它们相等，说明找到了目标值，返回 true。

7. 如果矩阵中的元素小于 target，则更新 low 为 mid + 1，以排除左半边搜索范围。

8. 如果矩阵中的元素大于 target，则更新 high 为 mid - 1，以排除右半边搜索范围。

9. 循环结束后，如果没有找到目标值，返回 false，指示目标值不在矩阵中。

这个算法利用二分查找的思想，以 O(log(m*n)) 的时间复杂度来高效地在二维矩阵中查找目标值。

Python 版本解题思路

1. 首先，检查输入的矩阵是否为空。如果矩阵为空，直接返回 False，因为无法在空矩阵中查找目标值。

2. 获取矩阵的行数（rows）和列数（cols），用于后续计算。

3. 初始化两个指针，low 和 high，分别表示搜索范围的起始和结束。low 初始化为0，high 初始化为矩阵中元素总数减1。

4. 进入一个循环，条件是 low 小于等于 high。这个循环是二分查找的核心。

5. 在循循环中，首先计算中间索引 mid，以将搜索范围分成两半。这是通过 low + (high - low) // 2 来实现的。

6. 然后，使用整除和取模运算，将 mid 转换为矩阵中的行和列索引，即 divmod(mid, cols)。

7. 比较矩阵中索引为 row 和 col 的元素与目标值 target。如果它们相等，说明找到了目标值，返回 True。

8. 如果矩阵中的元素小于 target，则更新 low 为 mid + 1，以排除左半边搜索范围。

9. 如果矩阵中的元素大于 target，则更新 high 为 mid - 1，以排除右半边搜索范围。

10. 循环结束后，如果没有找到目标值，返回 False，指示目标值不在矩阵中。

这个算法使用二分查找的思想，以 O(log(m*n)) 的时间复杂度来高效地在二维矩阵中查找目标值。

Java 版本解题思路

1. 首先，检查输入的矩阵是否为空。如果矩阵为空，直接返回 false，因为无法在空矩阵中查找目标值。

2. 获取矩阵的行数（rows）和列数（cols），用于后续计算。

3. 初始化两个指针，low 和 high，分别表示搜索范围的起始和结束。low 初始化为0，high 初始化为矩阵中元素总数减1。

4. 进入一个循环，条件是 low 小于等于 high。这个循环是二分查找的核心。

5. 在循环中，首先计算中间索引 mid，以将搜索范围分成两半。这是通过 low + (high - low) / 2 来实现的。

6. 然后，使用整数除法和取模运算，将 mid 转换为矩阵中的行和列索引，即 mid / cols 和 mid % cols。

7. 比较矩阵中索引为 row 和 col 的元素与目标值 target。如果它们相等，说明找到了目标值，返回 true。

8. 如果矩阵中的元素小于 target，则更新 low 为 mid + 1，以排除左半边搜索范围。

9. 如果矩阵中的元素大于 target，则更新 high 为 mid - 1，以排除右半边搜索范围。

10. 循环结束后，如果没有找到目标值，返回 false，指示目标

代码

Go

func searchMatrix(matrix [][]int, target int) bool {
    // 函数名：searchMatrix，接收两个参数，一个是二维整数数组 matrix，另一个是目标值 target。
    
    if len(matrix) == 0 {
        // 如果二维数组 matrix 为空，也就是没有元素，返回 false。
        return false
    }
    
    m, low, high := len(matrix[0]), 0, len(matrix[0])*len(matrix)-1
    // 定义变量 m，表示矩阵的列数；low 和 high 用于二分查找，初始化 low 为 0，high 为 (矩阵行数 * 列数 - 1)。
    
    for low <= high {
        // 进入一个循环，直到 low 大于 high 为止。
        
        mid := low + (high-low)>>1
        // 计算中间位置的索引 mid，这里采用二分查找的方式。
        
        if matrix[mid/m][mid%m] == target {
            // 如果矩阵中索引为 mid/m 行，mid%m 列的元素等于目标值 target，返回 true。
            return true
        } else if matrix[mid/m][mid%m] > target {
            // 如果矩阵中索引为 mid/m 行，mid%m 列的元素大于目标值 target，将 high 更新为 mid - 1，缩小搜索范围。
            high = mid - 1
        } else {
            // 如果矩阵中索引为 mid/m 行，mid%m 列的元素小于目标值 target，将 low 更新为 mid + 1，缩小搜索范围。
            low = mid + 1
        }
    }
    
    // 若循环结束仍未找到目标值，返回 false。
    return false
}

Python

from typing import List

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix:
            return False

        rows, cols = len(matrix), len(matrix[0])
        low, high = 0, rows * cols - 1
        
        while low <= high:
            mid = low + (high - low) // 2
            row, col = divmod(mid, cols)
            
            if matrix[row][col] == target:
                return True
            elif matrix[row][col] < target:
                low = mid + 1
            else:
                high = mid - 1
        
        return False

Java

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0) {
            return false;
        }

        int rows = matrix.length;
        int cols = matrix[0].length;
        int low = 0;
        int high = rows * cols - 1;

        while (low <= high) {
            int mid = low + (high - low) / 2;
            int row = mid / cols;
            int col = mid % cols;

            if (matrix[row][col] == target) {
                return true;
            } else if (matrix[row][col] < target) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }

        return false;
    }
}

Cpp

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        if (matrix.empty() || matrix[0].empty()) {
            return false;
        }

        int rows = matrix.size();
        int cols = matrix[0].size();
        int low = 0;
        int high = rows * cols - 1;

        while (low <= high) {
            int mid = low + (high - low) / 2;
            int row = mid / cols;
            int col = mid % cols;

            if (matrix[row][col] == target) {
                return true;
            } else if (matrix[row][col] < target) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }

        return false;
    }
};

当阅读不同版本的解决方案时，理解每个版本所需的基础知识是很重要的。以下是每个版本的详细基础知识要求：

Go 版本

• 基础语法: 熟悉 Go 编程语言的基本语法，包括变量声明、条件语句、循环、函数定义、数组和切片等。

• 数组和切片: 了解 Go 中的数组和切片，以便理解如何处理二维矩阵。

• 二分查找: 理解二分查找算法的原理和实现方式，包括如何计算中间索引并根据比较结果更新搜索范围。

Python 版本

• 基础语法: 熟悉 Python 编程语言的基本语法，包括变量声明、条件语句、循环、函数定义、列表等。

• 列表和元组: 了解 Python 中的列表和元组，因为它们可以用于表示二维矩阵。

• 整除和取模运算: 理解如何使用整除和取模运算 (// 和 %) 来将一维索引转换为二维坐标。

Java 版本

• 基础语法: 熟悉 Java 编程语言的基本语法，包括类、方法、条件语句、循环、数组等。

• 二维数组: 了解 Java 中的二维数组，包括如何声明、初始化和访问元素。

• 整数运算: 理解如何使用整数运算来计算中间索引以及整数除法和取模运算 (/ 和 %) 以将一维索引转换为二维坐标。

C++ 版本

• 基础语法: 熟悉 C++ 编程语言的基本语法，包括类、方法、条件语句、循环、数组等。

• 二维向量: 了解 C++ 中的二维向量（vector of vectors），包括如何声明、初始化和访问元素。

• 整数运算: 理解如何使用整数运算来计算中间索引以及整数除法和取模运算 (/ 和 %) 以将一维索引转换为二维坐标。

无论选择哪个版本，理解基本的编程概念、数组和列表、循环和条件语句、二分查找等算法，以及索引计算的原理都是解决问题的关键要素。熟练运用这些知识将有助于理解和编写类似的算法。

75. Sort Colors

题目

Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue.

Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.

Note: You are not suppose to use the library’s sort function for this problem.

Example 1:

Input: [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]

Follow up:

• A rather straight forward solution is a two-pass algorithm using counting sort.
  First, iterate the array counting number of 0’s, 1’s, and 2’s, then overwrite array with total number of 0’s, then 1’s and followed by 2’s.
• Could you come up with a one-pass algorithm using only constant space?

题目大意

抽象题意其实就是排序。这题可以用快排一次通过。

解题思路

题目末尾的 Follow up 提出了一个更高的要求，能否用一次循环解决问题？这题由于数字只会出现 0，1，2 这三个数字，所以用游标移动来控制顺序也是可以的。具体做法：0 是排在最前面的，所以只要添加一个 0，就需要放置 1 和 2。1 排在 2 前面，所以添加 1 的时候也需要放置 2 。至于最后的 2，只用移动游标即可。

这道题可以用计数排序，适合待排序数字很少的题目。用一个 3 个容量的数组分别计数，记录 0，1，2 出现的个数。然后再根据个数排列 0，1，2 即可。时间复杂度 O(n)，空间复杂度 O(K)。这一题 K = 3。

这道题也可以用一次三路快排。数组分为 3 部分，第一个部分都是 0，中间部分都是 1，最后部分都是 2 。
以下是每个版本的解题思路的详细介绍：

Python 版本：

• 解题思路： 这个解决方案采用了一种双指针的方法，其中zero指针用于跟踪0的位置，one指针用于跟踪1的位置。初始时，两个指针都在数组的开头。

• 遍历数组： 通过遍历数组中的每个元素，首先将当前元素的值设置为2，以表示最终排序的数组中的元素都是2。

• 处理0和1： 如果当前元素的值小于等于1（即0或1），将其设置为1，并将one指针向后移动。

• 处理0： 如果当前元素的值为0，将其设置为0，并将zero指针向后移动。这样，0将排在1的前面。

• 结束： 完成遍历后，数组将按照所需的顺序排序：首先是0，然后是1，最后是2。

Java 版本：

• 解题思路： Java版本的解决方案也采用了双指针的方法，其中zero指针用于跟踪0的位置，one指针用于跟踪1的位置，以及two指针用于跟踪2的位置。

• 遍历数组： 通过遍历数组中的每个元素，首先将当前元素的值设置为2，以表示最终排序的数组中的元素都是2。

• 处理0： 如果当前元素的值为0，使用swap交换zero指针和one指针处的元素，并将zero指针和one指针都向后移动。这将把0排在1的前面。

• 处理2： 如果当前元素的值为2，使用swap交换one指针和two指针处的元素，并将two指针向前移动。这将把2排在1的后面。

• 结束： 完成遍历后，数组将按照所需的顺序排序：首先是0，然后是1，最后是2。

C++ 版本：

• 解题思路： C++版本的解决方案也采用了双指针的方法，其中zero指针用于跟踪0的位置，one指针用于跟踪1的位置，以及two指针用于跟踪2的位置。

• 遍历数组： 通过遍历数组中的每个元素，首先将当前元素的值设置为2，以表示最终排序的数组中的元素都是2。

• 处理0： 如果当前元素的值为0，使用std::swap()交换zero指针和one指针处的元素，并将zero指针和one指针都向后移动。这将把0排在1的前面。

• 处理2： 如果当前元素的值为2，使用std::swap()交换one指针和two指针处的元素，并将two指针向前移动。这将把2排在1的后面。

• 结束： 完成遪历后，数组将按照所需的顺序排序：首先是0，然后是1，最后是2。

Go 版本：

• 解题思路： Go版本的解决方案同样使用了双指针的方法。其中，zero指针用于跟踪0的位置，one指针用于跟踪1的位置。

• 遍历数组： 通过遍历数组中的每个元素，首先将当前元素的值设置为2，以表示最终排序的数组中的元素都是2。

• 处理0： 如果当前元素的值小于等于1，将其设置为1，并将one指针向后移动。

• 处理0： 如果当前元素的值为0，将其设置为0，并将zero指针向后移动。这将把0排在1的前面。

• 结束： 完成遍历后，数组将按照所需的顺序排序：首先是0，然后是1，最后是2。

总的来说，所有版本的代码采用了双指针的方法，通过一次遍历数组并根据元素的值来重新排列数组中的元素，以实现题目所要求的排序。这种方法具有时间复杂度O(n)和常数空间复杂度，因此是高效的解决方案。

代码

Go

func sortColors(nums []int) {
	zero, one := 0, 0 // 初始化两个指针，分别表示数字0和数字1的位置
	for i, n := range nums {
		nums[i] = 2 // 将数组中的数字都设置为2，这是初始状态
		if n <= 1 {
			nums[one] = 1 // 如果当前数字是0或1，将其置为1，并将one指针向后移动
			one++
		}
		if n == 0 {
			nums[zero] = 0 // 如果当前数字是0，将其置为0，并将zero指针向后移动
			zero++
		}
	}
}

Python

from typing import List

class Solution:
    def sortColors(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        zero, one = 0, 0
        for i, n in enumerate(nums):
            nums[i] = 2
            if n <= 1:
                nums[one] = 1
                one += 1
            if n == 0:
                nums[zero] = 0
                zero += 1

Java

class Solution {
    public void sortColors(int[] nums) {
        int zero = 0, one = 0, two = nums.length - 1;
        while (one <= two) {
            if (nums[one] == 0) {
                int temp = nums[zero];
                nums[zero] = nums[one];
                nums[one] = temp;
                zero++;
                one++;
            } else if (nums[one] == 2) {
                int temp = nums[one];
                nums[one] = nums[two];
                nums[two] = temp;
                two--;
            } else {
                one++;
            }
        }
    }
}

Cpp

class Solution {
public:
    void sortColors(vector& nums) {
        int zero = 0, one = 0, two = nums.size() - 1;
        while (one <= two) {
            if (nums[one] == 0) {
                swap(nums[zero], nums[one]);
                zero++;
                one++;
            } else if (nums[one] == 2) {
                swap(nums[one], nums[two]);
                two--;
            } else {
                one++;
            }
        }
    }
};

当介绍不同版本的代码时，我们将分别讨论每个版本的代码中所需的基础知识。

Python 版本：

1. Python基础知识： 需要熟悉Python的基本语法、数据类型、列表（List）的使用，循环（for循环）和条件语句（if语句）的使用。此外，需要了解Python的面向对象编程（OOP）概念，因为代码中使用了类和方法。

2. LeetCode题目理解： 需要理解LeetCode的题目，包括输入参数和要求的输出，以便能够编写相应的解决方案。

3. 数组操作： 理解如何遍历和操作数组元素，以及如何使用enumerate()函数来同时获取元素和索引。

Java 版本：

1. Java基础知识： 需要对Java编程语言有基本的了解，包括类、方法、变量的声明和使用。理解循环和条件语句的使用也是必要的。

2. LeetCode题目理解： 同样需要理解LeetCode的题目要求，包括输入和输出的格式。

3. 数组操作： 了解如何遍历和操作数组元素，以及如何使用数组的下标。

C++ 版本：

1. C++基础知识： 需要了解C++编程语言的基本语法，包括类、方法、变量的声明和使用。了解循环和条件语句的使用也是必要的。

2. LeetCode题目理解： 需要理解LeetCode的题目要求，包括输入和输出的格式。

3. 数组操作： 了解如何遍历和操作数组元素，以及如何使用数组的下标。在C++中，可以使用std::swap()函数来交换数组元素。

4. 类和方法的使用： 了解如何定义和使用类以及类的方法。在这个示例中，使用了一个类来包装排序方法。

Go 版本：

1. Go基础知识： 需要对Go编程语言有一些基本了解，包括函数、切片（slice）、for循环和if语句的使用。

2. LeetCode题目理解： 同样需要理解LeetCode的题目要求，包括输入和输出的格式。

3. 切片（slice）的使用： 了解如何操作和修改切片，以及如何通过索引访问切片中的元素。

总的来说，不管是哪个编程语言版本，理解LeetCode题目、数组操作和基本编程语法都是解决问题的基础。不同语言的语法和特性可能略有不同，但解决问题的思路和算法通常是相似的。

76. Minimum Window Substring

题目

Given a string S and a string T, find the minimum window in S which will contain all the characters in T in complexity O(n).

Example:

Input: S = "ADOBECODEBANC", T = "ABC"
Output: "BANC"

Note:

• If there is no such window in S that covers all characters in T, return the empty string “”.
• If there is such window, you are guaranteed that there will always be only one unique minimum window in S.

题目大意

给定一个源字符串 s，再给一个字符串 T，要求在源字符串中找到一个窗口，这个窗口包含由字符串各种排列组合组成的，窗口中可以包含 T 中没有的字符，如果存在多个，在结果中输出最小的窗口，如果找不到这样的窗口，输出空字符串。

解题思路

这一题是滑动窗口的题目，在窗口滑动的过程中不断的包含字符串 T，直到完全包含字符串 T 的字符以后，记下左右窗口的位置和窗口大小。每次都不断更新这个符合条件的窗口和窗口大小的最小值。最后输出结果即可。

以下是每个版本的解题思路的详细介绍：

Go 版本：

1. 创建两个数组 tFreq 和 sFreq 用于记录字符频率，初始化一些变量如 result、left、right、finalLeft、finalRight、minW 和 count 。

2. 遍历字符串 T，统计每个字符的频率并存储在 tFreq 中。

3. 使用滑动窗口来在字符串 S 中查找包含所有 T 字符的最小窗口。

4. 移动右指针，不断更新 sFreq 中字符频率，同时增加 count 计数，直到包含所有 T 字符。

5. 一旦找到包含 T 的子串，计算窗口宽度，并更新 finalLeft、finalRight 和 minW。

6. 移动左指针，不断更新 sFreq 中字符频率，同时减少 count 计数，缩小窗口。

7. 最终，返回最小窗口的内容。

Python 版本：

1. 创建一个字典 need 用于存储字符串 T 中字符的频率。

2. 初始化变量 i、count 和 res。i 用于指示左窗口边界，count 用于计算还需要多少个字符，res 用于存储最小窗口的起始和结束位置。

3. 遍历字符串 S，右指针从左到右移动，统计字符频率，同时减少 need 中相应字符的频率。

4. 当 count 变为零时，表示找到一个包含 T 所有字符的窗口。

5. 移动左指针 i 缩小窗口，直到无法再缩小为止。在此过程中，继续更新 res 记录最小窗口的范围。

6. 最终，返回最小窗口的内容。

Java 版本：

1. 获取字符串 S 和 T 的长度，并初始化字符频率数组 count，以及字符总数 time。

2. 遍历字符串 T，统计每个字符的频率并增加 time。

3. 初始化左指针 left 和窗口长度 len，以及结果字符串 ans。

4. 遍历字符串 S，右指针从左到右移动，处理字符频率和计数。

5. 当窗口包含 T 中所有字符时，缩小窗口左边界，直到无法再缩小。在此过程中，不断更新 ans 记录最小窗口的范围。

6. 最终，返回最小窗口的内容。

C++ 版本：

1. 创建两数组 tFreq 和 sFreq 用于记录字符频率，并初始化一些变量如 result、left、right、finalLeft、finalRight、minW 和 count。

2. 遍历字符串 T，统计每个字符的频率并存储在 tFreq 中。

3. 使用滑动窗口来在字符串 S 中查找包含所有 T 字符的最小窗口。

4. 移动右指针，不断更新 sFreq 中字符频率，同时增加 count 计数，直到包含所有 T 字符。

5. 一旦找到包含 T 的子串，计算窗口宽度，并更新 finalLeft、finalRight 和 minW。

6. 移动左指针，不断更新 sFreq 中字符频率，同时减少 count 计数，缩小窗口。

7. 最终，返回最小窗口的内容。

这四个版本的解题思路都是使用滑动窗口技巧，通过不断移动左右指针来找到包含所有目标字符的最小窗口。不同编程语言的实现细节和语法略有不同，但基本思路相同。理解这些思路和对应编程语言的基础知识将帮助您更好地理解和修改这些代码。

代码

Go

func minWindow(s string, t string) string {
	// 如果输入的s或t为空字符串，则直接返回空字符串
	if s == "" || t == "" {
		return ""
	}
	
	// 定义两个数组tFreq和sFreq，用于记录字符频率
	var tFreq, sFreq [256]int
	result, left, right, finalLeft, finalRight, minW, count := "", 0, -1, -1, -1, len(s)+1, 0

	// 遍历字符串t，统计每个字符的频率并存储在tFreq中
	for i := 0; i < len(t); i++ {
		tFreq[t[i]-'a']++
	}

	// 开始滑动窗口操作
	for left < len(s) {
		// 如果右指针在字符串s范围内且字符计数count小于字符串t的长度
		if right+1 < len(s) && count < len(t) {
			// 移动右指针，并更新sFreq中字符频率
			sFreq[s[right+1]-'a']++
			// 如果字符s[right+1]的频率不超过t中的频率，则增加计数count
			if sFreq[s[right+1]-'a'] <= tFreq[s[right+1]-'a'] {
				count++
			}
			right++
		} else {
			// 当找到包含t的子串时，计算窗口宽度
			if right-left+1 < minW && count == len(t) {
				minW = right - left + 1
				finalLeft = left
				finalRight = right
			}
			// 移动左指针，更新sFreq中字符频率
			if sFreq[s[left]-'a'] == tFreq[s[left]-'a'] {
				count--
			}
			sFreq[s[left]-'a']--
			left++
		}
	}
	
	// 如果找到了包含t的子串，根据finalLeft和finalRight提取结果
	if finalLeft != -1 {
		result = string(s[finalLeft : finalRight+1])
	}
	return result
}

Python

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        need = collections.defaultdict(int)  # 创建一个用于存储字符串 t 中字符频率的字典
        for c in t:
            need[c] += 1  # 统计字符串 t 中字符的频率
        
        i = 0
        count = len(t)  # 初始化字符计数
        res = (0, len(s))  # 初始化结果的起始位置和结束位置，初始设为整个字符串的范围
        
        for j, c in enumerate(s):
            if need[c] > 0:
                count -= 1  # 当字符 c 在 need 中的频率大于零时，减少计数
            need[c] -= 1  # 减少 need 中字符 c 的频率
            
            if count == 0:  # 当字符计数等于零时，表示找到包含 t 的窗口
                while True:
                    if need[s[i]] == 0:
                        break
                    need[s[i]] += 1
                    i += 1
                
                if (j - i) < (res[1] - res[0]):  # 计算窗口宽度，如果小于当前最小窗口宽度，则更新结果
                    res = (i, j)
                
                need[s[i]] += 1
                count += 1
                i += 1
        
        return "" if res[1] == len(s) else s[res[0]:res[1] + 1]  # 返回最短窗口的内容，如果找不到则返回空字符串

Java

class Solution {
    public String minWindow(String s, String t) {
        int sLen = s.length();  // 获取字符串 s 的长度
        int tLen = t.length();  // 获取字符串 t 的长度
        if (sLen < tLen) {
            return "";
        }
        int[] count = new int[64];  // 用于记录字符频率的数组
        int time = 0;  // 字符串 t 中字符的总数
        for (char c : t.toCharArray()) {
            count[c - 'A']++;  // 统计字符串 t 中字符的频率
            time++;
        }
        int left = 0, len = 0;  // 初始化左指针和长度
        char[] sArr = s.toCharArray();
        String ans = "";  // 用于存储最短窗口结果的字符串
        for (int i = 0; i < sLen; i++) {
            int index = sArr[i] - 'A';  // 获取当前字符在 count 数组中的索引
            if (count[index] > 0) {
                len++;
            }
            count[index]--;
            while (len == time && count[sArr[left] - 'A'] < 0) {
                count[sArr[left] - 'A']++;
                left++;  // 移动左指针
            }
            if (len == time && (ans == "" || i - left + 1 < ans.length())) {
                ans = s.substring(left, i + 1);  // 更新最短窗口的结果
            }
        }
        return ans;  // 返回最短窗口的内容
    }
}

Cpp

class Solution {
public:
    string minWindow(string s, string t) {
        if (s.empty() || t.empty()) {
            return "";
        }

        vector tFreq(256, 0);
        vector sFreq(256, 0);
        string result = "";
        int left = 0, right = -1, finalLeft = -1, finalRight = -1, minW = s.size() + 1, count = 0;

        for (char c : t) {
            tFreq[c]++;
        }

        while (left < s.size()) {
            if (right + 1 < s.size() && count < t.size()) {
                right++;
                sFreq[s[right]]++;
                if (sFreq[s[right]] <= tFreq[s[right]]) {
                    count++;
                }
            } else {
                if (right - left + 1 < minW && count == t.size()) {
                    minW = right - left + 1;
                    finalLeft = left;
                    finalRight = right;
                }
                if (sFreq[s[left]] == tFreq[s[left]]) {
                    count--;
                }
                sFreq[s[left]]--;
                left++;
            }
        }

        if (finalLeft != -1) {
            result = s.substr(finalLeft, finalRight - finalLeft + 1);
        }
        return result;
    }
};

当使用不同编程语言（Go、Python、Java、C++）来解决特定问题时，需要了解每种编程语言的基础知识以理解代码。以下是针对每个版本的详细基础知识介绍：

Go 版本：

1. 基本语法和数据类型： 需要了解 Go 的基本语法，包括变量声明、数据类型（如字符串、整数、数组、切片、映射等）、运算符等。

2. 函数和方法： 理解函数和方法的声明、调用以及参数传递方式。

3. 数组和切片： 理解 Go 中的数组和切片，以及它们的使用方式和区别。

4. 循环和条件语句： 理解 Go 中的循环（如 for 循环）和条件语句（如 if 语句）的使用。

5. 结构体和方法： 了解如何定义结构体和关联的方法。

6. 并发和协程： 了解 Go 中的并发编程概念，如协程（goroutines）和通道（channels）。

Python 版本：

1. 基本语法和数据类型： 理解 Python 的基本语法，包括变量声明、数据类型（如字符串、整数、列表、字典等）、运算符等。

2. 函数： 了解如何定义函数、函数参数传递、函数的返回值以及函数的作用域。

3. 列表和字典： 理解 Python 中的列表和字典，以及它们的用途和方法。

4. 循环和条件语句： 了解 Python 中的循环（如 for 循环）和条件语句（如 if 语句）的使用。

5. 类和对象： 了解如何定义类和创建对象，以及类的方法和属性。

6. 文件操作： 了解如何打开、读取和写入文件。

7. 模块和包： 了解 Python 中模块和包的概念，以及如何导入和使用它们。

Java 版本：

1. 基本语法和数据类型： 需要了解 Java 的基本语法，包括变量声明、数据类型（如整数、字符串、数组等）、运算符等。

2. 类和对象： 了解如何定义类和创建对象，以及类的方法和属性。

3. 循环和条件语句： 理解 Java 中的循环（如 for 循环）和条件语句（如 if 语句）的使用。

4. 集合和数据结构： 了解 Java 中的集合框架，如列表、映射、集合等，以及它们的使用。

5. 文件操作： 了解如何处理文件的读取和写入。

6. 异常处理： 了解如何捕获和处理异常情况。

7. 多线程和并发： 了解 Java 中多线程编程和并发编程的基本概念。

C++ 版本：

1. 基本语法和数据类型： 需要了解 C++ 的基本语法，包括变量声明、数据类型（如整数、字符串、数组等）、运算符等。

2. 函数： 了解如何定义函数、函数参数传递、函数的返回值以及函数的重载。

3. STL（标准模板库）： 了解 C++ 中的STL容器（如向量、映射、队列等）和STL算法。

4. 循环和条件语句： 理解 C++ 中的循环（如 for 循环）和条件语句（如 if 语句）的使用。

5. 类和对象： 了解如何定义类和创建对象，以及类的方法和属性。

6. 文件操作： 了解如何处理文件的读取和写入。

7. 异常处理： 了解如何捕获和处理异常情况。

8. 指针和内存管理： 了解 C++ 中指针的使用和内存管理，包括动态内存分配和释放。

以上是每个版本中所需的基本知识要点，您可以根据选择的编程语言深入学习相关主题以更好地理解和修改给出的代码。这将有助于您在解决类似问题时编写自己的代码或进行定制化的开发。

77. Combinations

题目

Given two integers n and k, return all possible combinations of k numbers out of 1 … n.

Example:

Input: n = 4, k = 2
Output:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

题目大意

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

解题思路

• 计算排列组合中的组合，用 DFS 深搜即可，注意剪枝
• 下面分别介绍每个版本的解题思路：

Go 版本解题思路：

1. 组合问题：给定一个范围从 1 到 n，要求生成所有长度为 k 的组合。

2. DFS 深度搜索：使用深度优先搜索 (DFS) 来生成所有可能的组合。

3. 剪枝 (Pruning)：在搜索过程中，采用剪枝策略来减少不必要的搜索。如果当前已选的元素个数超过 k，则停止向下搜索，这是剪枝的一种情况。

4. 遍历范围：从 1 开始遍历到 n - (k - len(path)) + 1，其中 len(path) 是当前已选元素的个数。这个范围的选择是为了确保生成的组合不会超出 k 个元素。

5. 组合存储：用一个切片 (path) 来存储当前正在生成的组合，当达到长度为 k 时，将其复制并添加到结果中。

Python 版本解题思路：

1. 组合问题：给定一个范围从 1 到 n，要求生成所有长度为 k 的组合。

2. DFS 深度搜索：使用深度优先搜索 (DFS) 来生成所有可能的组合。

3. Memoization：采用 memoization 技巧，避免重复计算相同子问题，提高递归性能。

4. 递归函数：定义递归函数 dfsHelper(start, k)，其中 start 表示当前数字的起始点，k 表示剩余需要选的数字个数。

5. 基本情况：在递归函数中，处理基本情况。当 k 为 0 时，返回一个包含空列表的列表，表示找到一个组合。

6. 生成组合：递归地生成组合，包括当前数字 (start) 和不包括当前数字两种情况。

7. 返回结果：返回生成的组合结果。

Java 版本解题思路：

1. 组合问题：给定一个范围从 1 到 n，要求生成所有长度为 k 的组合。

2. 深度优先搜索 (DFS)：使用深度优先搜索 (DFS) 来生成所有可能的组合。

3. 抽象类和匿名子类：在 Java 中，定义了一个抽象类来封装组合生成的逻辑，并创建一个匿名子类来提供更方便的接口。

4. 递归函数：定义递归函数 dfsHelper(parentDepth, n, k)，其中 parentDepth 表示上一级递归的深度，n 表示总的数字范围，k 表示还需要选择的数字个数。

5. 基本情况：在递归函数中，处理基本情况。当 k 为 0 时，将当前组合添加到结果中。

6. 生成组合：递归地生成组合，包括当前数字和不包括当前数字两种情况。

7. 返回结果：返回生成的组合结果。

C++ 版本解题思路：

1. 组合问题：给定一个范围从 1 到 n，要求生成所有长度为 k 的组合。

2. DFS 深度搜索：使用深度优先搜索 (DFS) 来生成所有可能的组合。

3. Lambda 表达式：在 C++ 中，使用 lambda 表达式来定义递归函数。

4. 递归函数：定义递归函数 dfsHelper(parentDepth)，其中 parentDepth 表示上一级递归的深度。

5. 基本情况：在递归函数中，处理基本情况。当当前组合的长度等于 k 时，将其添加到结果中。

6. 生成组合：递归地生成组合，包括当前数字和不包括当前数字两种情况。

7. 返回结果：返回生成的组合结果。

这些是不同版本的解题思路的关键要点，它们共同使用深度优先搜索 (DFS) 和递归来生成所有可能的组合，同时在某些版本中还使用了剪枝或 memoization 来优化性能。

代码

Go

func combine(n int, k int) [][]int {
    result := make([][]int, 0)
    path := make([]int, 0)

    var backtracking func(n,k,startIndex int)
    backtracking = func(n,k,startIndex int) {
        if len(path) == k {
            tmp := make([]int, k)
            copy(tmp, path)
            result = append(result, tmp)
        }
        
        for i:=startIndex; i <= n - (k - len(path)) + 1; i++ {
            if len(path) > k{  // 剪枝
                break
            }
            path = append(path, i)
            backtracking(n,k,i+1)
            path = path[:len(path)-1]
        }
    }

    backtracking(n,k,1)
    return result
}

Python

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        memo = {}
        def dfs(start, k):
            if (start, k) in memo:
                return memo[(start, k)]

            if k == 0:
                return [[]]
            if start > n:
                return []
            if start == n:
                return [[n]] if k == 1 else []
            
            res = []

            # Generate combinations that include the "start" element
            for rest in dfs(start + 1, k - 1):
                res.append([start] + rest)

            # Add combinations that don't include the "start" element
            res.extend(dfs(start + 1, k))
            
            memo[(start, k)] = res
            return res
        
        return dfs(1, k)

Java

// 导入Java的AbstractList类
import java.util.AbstractList;

// 创建一个Solution类
class Solution {
    private List> res;

    // 定义公共方法combine，用于生成组合
    public List> combine(int n, int k) {
        // 返回一个AbstractList的匿名子类实例
        return new AbstractList>() {
            @Override
            public int size() {
                // 初始化并返回结果的大小
                init();
                return res.size();
            }

            @Override
            public List get(int index) {
                // 初始化并返回指定索引的组合
                init();
                return res.get(index);
            }

            // 初始化组合的计算
            protected void init() {
                if (res != null)
                    return;
                res = new ArrayList>();
                dfsHelper(-1, n, k, res, new ArrayList());
            }
        };
    }

    // 定义深度优先搜索的辅助方法
    private void dfsHelper(int parentDepth, int n, int k, List> res, List subset) {
        parentDepth += 1;
        if (parentDepth == n) {
            if (subset.size() == k) {
                // 如果subset的大小为k，将其添加到结果res中
                res.add(new ArrayList(subset));
            }
        } else {
            /* <-.前序决策左、右子结点: */

            // 递归调用dfsHelper，不包含当前数字
            dfsHelper(parentDepth, n, k, res, subset);

            // 将当前数字加入subset
            subset.add(parentDepth + 1);
            // 递归调用dfsHelper，包含当前数字
            dfsHelper(parentDepth, n, k, res, subset);
            // 移除最后添加的数字，以便尝试下一个数字
            subset.remove(subset.size() - 1);
        }
    }
}

Cpp

class Solution {
public:
    vector> combine(int n, int k) {
        vector> res;
        vector subset;

        function dfsHelper = [&](int parentDepth) {
            if (subset.size() == k) {
                res.push_back(subset);
                return;
            }
            for (int i = parentDepth + 1; i <= n; i++) {
                subset.push_back(i);
                dfsHelper(i);
                subset.pop_back();
            }
        };

        dfsHelper(0);
        return res;
    }
};

理解不同版本的代码需要一些基本的编程和算法知识。以下是每个版本所需的基础知识的详细介绍：

Go 版本：

1. Go 编程语言：理解 Go 语言的基础语法，数据结构，以及函数的定义和使用。

2. 递归和深度优先搜索 (DFS)：了解递归的概念和如何使用递归来解决问题。此外，理解深度优先搜索 (DFS) 是如何应用在这个代码中的。

3. 切片 (Slices)：Go 中的切片是动态数组，它的长度可以动态变化。在这个代码中，切片被用于存储部分组合结果。

4. 剪枝 (Pruning)：剪枝是一种优化技巧，用于减少搜索空间。在这个代码中，剪枝用于提前终止搜索不可能生成有效组合的情况。

Python 版本：

1. Python 编程语言：理解 Python 语言的基础语法，包括列表、字典、函数等。

2. 递归和深度优先搜索 (DFS)：了解递归的概念和如何使用递归来解决问题。在这个代码中，深度优先搜索 (DFS) 用于生成组合。

3. Memoization：Memoization 是一种优化技巧，用于存储已计算的结果以避免重复计算。在这个代码中，memoization 被用于提高递归函数的性能。

Java 版本：

1. Java 编程语言：理解 Java 语言的基础语法，包括类、方法、集合类等。

2. 递归和深度优先搜索 (DFS)：了解递归的概念和如何使用递归来解决问题。在这个代码中，深度优先搜索 (DFS) 用于生成组合。

3. 抽象类 (Abstract Class)：了解抽象类的概念，它在这个代码中用于创建一个抽象的数据结构。

4. 匿名子类 (Anonymous Inner Class)：理解匿名子类的概念，它用于在代码中创建一个匿名的子类。

C++ 版本：

1. C++ 编程语言：理解 C++ 语言的基础语法，包括类、函数、lambda 表达式等。

2. 递归和深度优先搜索 (DFS)：了解递归的概念和如何使用递归来解决问题。在这个代码中，深度优先搜索 (DFS) 用于生成组合。

3. Lambda 表达式：理解 C++ 中的 lambda 表达式，它在这个代码中用于定义递归函数。

这些基础知识是理解和分析这些代码的关键要点。如果您对其中的某个概念不熟悉，建议深入学习相关的编程和算法知识，以便更好地理解这些代码。