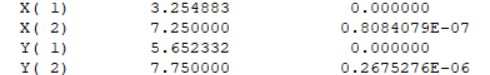数学建模之非线性规划与目标规划
EverydayOneCat
Sunday!
️️️️️️️️️️️️

知识点
1.优化模型建立注意事项
- 决策变量尽量使通量,其标志是下标尽量的多
- 模型中尽量使用连加号
- 同类型的约束统一成一个表达式
- 优化模型尽量不要用数字,包括已知变量
- 决策变量宜多不宜少
- 模型不要用分式,更不能将变量放置分母
- 决策变量要全部或部分出现在目标函数以及所有约束条件当中
- 建立优化模型要顾及自己编程的能力
2.非线性规划
2.1下料问题
客户需求:4米50根、5米10根、6米20根、8米15根。现有19米的原钢管可以购买。由于采用不同切割模式太多,会增加生产和管理成本,规定切割模式不能超过3种。如何下料最节省?
对大规模问题,用模型的约束条件界定合理模式
决策变量:
xi ~按第i 种模式切割的原料钢管根数(i=1,2,3)
r1i, r2i, r3i, r4i ~ 第i 种切割模式下,每根原料钢管生产4米、5米、6米和8米长的钢管的数量

增加约束,缩小可行域,便于求解


根据模型编写Lingo代码:
model:
Title 钢管下料- 最小化钢管根数的LINGO模型;
SETS:
NEEDS/1..4/:LENGTH,NUM;
CUTS/1..3/:X;
PATTERNS(NEEDS,CUTS):R;
ENDSETS
DATA:
LENGTH=4 5 6 8;
NUM=50 10 20 15;
CAPACITY=19;
ENDDATA
min=@SUM(CUTS(I): X(I) );
@FOR(NEEDS(I): @SUM(CUTS(J): X(J)*R(I,J) ) >NUM(I) ); !满足需求约束;
@FOR(CUTS(J): @SUM(NEEDS(I): LENGTH(I)*R(I,J) ) CAPACITY-
@MIN(NEEDS(I):LENGTH(I)) ); !合理切割模式约束;
@SUM(CUTS(I): X(I) ) >26; @SUM(CUTS(I): X(I) ) <31; !人为增加约束;
@FOR(CUTS(I)|I#LT#@SIZE(CUTS):X(I)>X(I+1) ); !人为增加约束;
@FOR(CUTS(J): @GIN(X(J)) ) ;
@FOR(PATTERNS(I,J): @GIN(R(I,J)) );
end
结果:用去原料钢管总根数为28根。
模式1:每根原料钢管切割成3根4米和1根6米钢管,共10根;
模式2:每根原料钢管切割成2根4米、1根5米和1根6米钢管,共10根;
模式3:每根原料钢管切割成2根8米钢管,共8根。原料钢管总根数为28根。
2.2料场的建立与运输
建筑工地的位置(用平面坐标a, b表示,距离单位:公里)及水泥日用量d(吨)下表给出。有两个临时料场位于P (5,1), Q (2, 7),日储量各有20吨。从A, B两料场分别向各工地运送多少吨水泥,使总的吨公里数最小。两个新的料场应建在何处,节省的吨公里数有多大?

这里的第一问就是典型的线性规划中的运输问题,上篇博文又讲,这里不过多赘述,我们主要来看第二问定点的问题。
我们设(ai,bi)为第i个工地的坐标,di为第i个工地的需求量。(xi,ji)为新的料场的坐标,cij为从第i个料场运到第j个工地的重量。
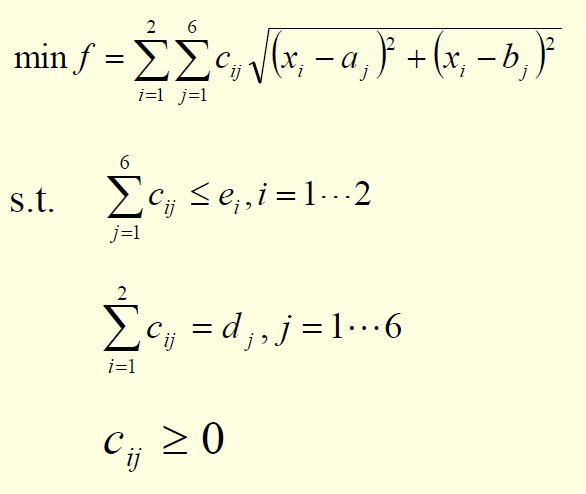
根据模型编写Lingo代码:(@bnd限定了范围)
model:
sets:
kc/1..2/:x,y,e;
gd/1..6/:a,b,d;
link(kc,gd):c;
endsets
data:
a=1.25,8.75,0.5,5.75,3,7.25;
b=1.25,0.75,4.75,5,6.5,7.75;
d=3,5,4,7,6,11; e=20,20;
enddata
!初始段:对集合属性定义初值(迭代算法的迭代初值);
init:
!初始点;
x,y=5,1,2,7;
endinit
min=@sum(link(i,j):c(i,j)*((x(i)-a(j))^2+(y(i)-b(j))^2)^(1/2));
@for(kc(i):@sum(gd(j):c(i,j))d(j));
@for(kc:@bnd(0.5,x,8.75));
@for(kc:@bnd(0.75,y,7.75));
end
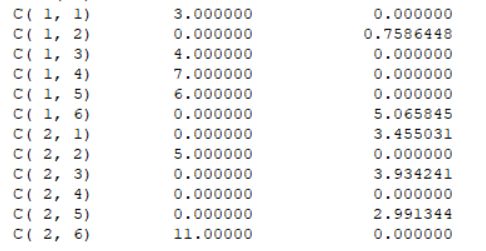
运行了一个小时中断得到的目前为止的最优解:
2.3投资组合问题
某三支股票在12年的收益如下:

解决如下问题:( 在希望风险小而获利大前提下考虑以上问题。)
(1)如果在1955年你有一笔资金投资这三种股票,并期望年收益率至少达到15%,那么你应当如何投资?
(2)如果还可以投资国库券,年收益率为5%,如何投资呢?分析投资组合与回报率以及风险的关系。
(3)如果你目前持有的股票比例为:A占50%,B占35%,C占15%,买卖股票按交易额的1%收取交易费,你会怎么办?
(1)如果在1955年你有一笔资金投资这三种股票,并期望年收益率至少达到15%,那么你应当如何投资?
第一问分析:
一种股票收益的均值衡量这种股票的平均收益状况
一种股票收益的方差衡量这种股票收益的波动幅度
两种股票收益的协方差表示他们之间的相关程度

假设股票A、B、C每年的收益率分别为R1,R2和R3
可计算数学期望:
ER1=0.0890833, ER2=0.213667, ER3=0.234583
协方差矩阵:

决策变量:x1投资股票A 、x2投资股票B 、x3投资股票C
约束条件:
- 资金全部用于投资这三种股票——x1, x2 , x3 ≥0,x1+x2 +x3 = 1
- 年收益率(的数学期望)不低于15%——x1ER1+x2ER2+x3ER3 ≥ 0.15
目标函数:年投资收益率的方差极小