数据库六大范式详解
候选码
某一属性组的值能唯一标识一个元组,而其子集不能,则称该属性组为候选码。若一个关系中有多个候选码,则选定其中一个为主码。
例如下图所示的学生表中,学号和姓名都可以唯一标识一个元组,故该表的候选码为学号和姓名,我们可以随便选定其中一个作为主码。
主属性
所有候选码的属性称为主属性。不包含在任何候选码中的属性称为非主属性或非码属性
在上面的学生表中,学号和姓名就是该关系的主属性,年龄和性别就是非主属性。
函数依赖
设R为任一给定的关系,如果对于R中属性X的每一个值,R中的属性Y只有唯一值与之对应,则称X函数决定Y或Y函数依赖于X,记作X——>Y。其中X称为决定因素。
通俗一点,就是给定一个X都有唯一的Y。可以理解为函数y=f(x);对于 任意的x 都有一个y,且y的取值有x决定。
例如:学号可以唯一确定一个学生的年龄、姓名等信息。
完全函数依赖
如果存在 X 属性组(注意是组,说明是联合主键)决定 唯一的 Y ,但 X 中的任一子集却不能决定唯一的 Y,则 Y 完全依赖于 X。
例如:学生的成绩由学生与课程共同决定。所以成绩完全依赖于学生与课程。
部分函数依赖
与完全函数依赖相反:如果存在 X 属性组(注意是组,说明是联合主键)决定 唯一的 Y ,且 X 中的任一子集都能能决定唯一的 Y,则 Y 部分依赖于X。
例如:在没有同名的情况下,学号与姓名都可以决定一个学生的年龄、性别等信息。
传递函数依赖
设 R 为任一给定关系, X Y Z 为其不同的属性子集,若 X —> Y 且 Y —>Z,则有 X —>Z,称为 Z 传递函数依赖于 X
例如:学号可以唯一确定一个系部,且系部可以唯一确定一个系主任。
什么是范式
范式来自英文Normal form,简称NF。要想设计—个好的关系,必须使关系满足一定的约束条件,此约束已经形成了规范,这就是我们俗称的范式。范式分成几个等级,一级比一级要求得严格。
范式的分类
目前关系数据库有六种范式:第一范式(1NF)、第二范式(2NF)、第三范式(3NF)、巴斯-科德范式(BCNF)、第四范式(4NF)和第五范式(5NF,又称完美范式)。满足最低要求的范式是第一范式(1NF)。在第一范式的基础上进一步满足更多规范要求的称为第二范式(2NF),其余范式以次类推。一般来说,数据库只需满足第三范式(3NF)就行了。
第一范式(1NF)
![]()
第二范式(2NF)
第二范式必须满足第一范式。
第二范式是指每个关系必须有一个(有且仅有一个)数据项作为主键,其他数据项与主键一一对应,即其他数据项完全依赖于主键。由此可知单主属性的关系均属于第二范式。
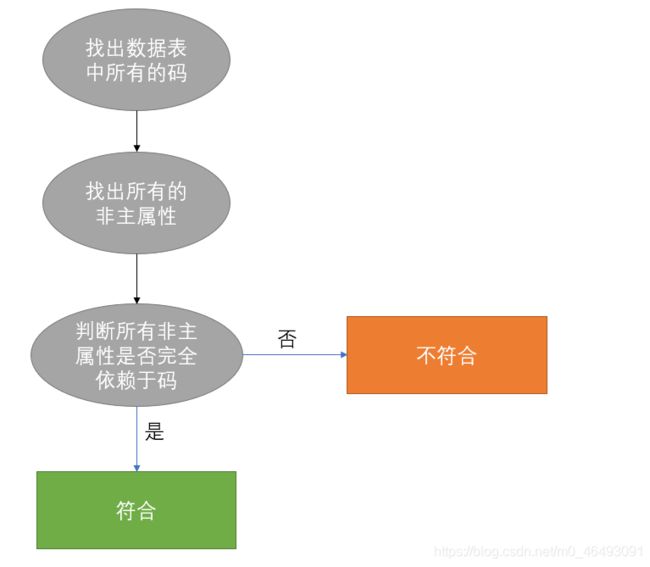
判断一个范式是否符合第二范式
第三范式(3NF)
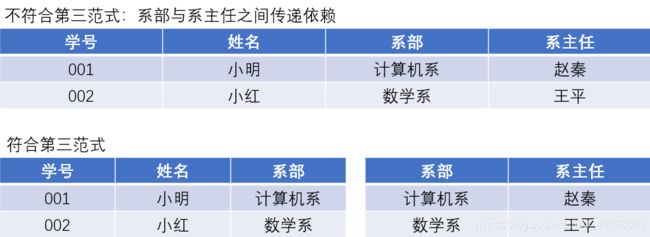
非主属性既不传递依赖于码,也不部分依赖于码。
理解:即在第二范式的基础上,消除了非主属性对码的传递依赖。
比如:
巴斯-科德范式(BCNF)
所有属性都完全依赖于码,每一个决定因素都包含码。
理解:一个满足BC范式的关系模式有:
- 所有非主属性对每一个码都是完全函数依赖;
- 所有主属性对每一个不包含它的码也是完全函数依赖;
- 没有任何属性完全函数依赖于非码的任何一组属性。
例如有关系模式C(Cno, Cname, Pcno),Cno, Cname, Pcno依次表示课程号、课程名、先修课。可知关系C只有一个码Cno,且没有任何属性对Cno部分函数依赖或传递函数依赖,所以关系C属于第三范式,同时Cno是C中的唯一决定因素,所以C也属于BC范式。
要了解 BCNF 范式,那么先看这样一个问题:
若:
- 某公司有若干个仓库;
- 每个仓库只能有一名管理员,一名管理员只能在一个仓库中工作;
- 一个仓库中可以存放多种物品,一种物品也可以存放在不同的仓库中。每种物品在每个仓库中都有对应的数量。
那么关系模式 仓库(仓库名,管理员,物品名,数量) 属于哪一级范式?
答:已知函数依赖集:仓库名 → 管理员,管理员 → 仓库名,(仓库名,物品名)→ 数量
码:(管理员,物品名),(仓库名,物品名)
主属性:仓库名、管理员、物品名
非主属性:数量
∵ 不存在非主属性对码的部分函数依赖和传递函数依赖。∴ 此关系模式属于3NF。
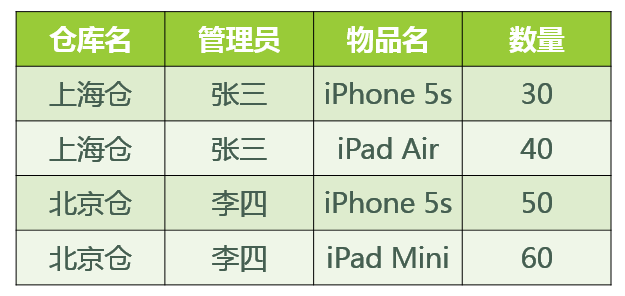
基于此关系模式的关系(具体的数据)可能如图所示:
好,既然此关系模式已经属于了 3NF,那么这个关系模式是否存在问题呢?我们来看以下几种操作:
- 先新增加一个仓库,但尚未存放任何物品,是否可以为该仓库指派管理员?——不可以,因为物品名也是主属性,根据实体完整性的要求,主属性不能为空。
- 某仓库被清空后,需要删除所有与这个仓库相关的物品存放记录,会带来什么问题?——仓库本身与管理员的信息也被随之删除了。
- 如果某仓库更换了管理员,会带来什么问题?——这个仓库有几条物品存放记录,就要修改多少次管理员信息。
从这里我们可以得出结论,在某些特殊情况下,即使关系模式符合 3NF 的要求,仍然存在着插入异常,修改异常与删除异常的问题,仍然不是 ”好“ 的设计。
造成此问题的原因:存在着主属性对于码的部分函数依赖与传递函数依赖。(在此例中就是存在主属性【仓库名】对于码【(管理员,物品名)】的部分函数依赖。
解决办法就是要在 3NF 的基础上消除主属性对于码的部分与传递函数依赖。
仓库(仓库名,管理员)
库存(仓库名,物品名,数量)
这样,之前的插入异常,修改异常与删除异常的问题就被解决了。
以上就是关于 BCNF 的解释。
第四范式(4NF)
定义:限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖。
理解: 显然一个关系模式是4NF,则必为BCNF。也就是说,当一个表中的非主属性互相独立时(3NF),这些非主属性不应该有多值,若有多值就违反了4NF。
四种范式之间存在如下关系
![]()
第五范式(5NF)
第五范式有以下要求:
(1)必须满足第四范式;
(2)表必须可以分解为较小的表,除非那些表在逻辑上拥有与原始表相同的主键。
第五范式是在第四范式的基础上做的进一步规范化。第四范式处理的是相互独立的多值情况,而第五范式则处理相互依赖的多值情况。