POJ 3264 Balanced Lineup 线段树 / 平方分割
一、题目大意
给出一个长度为 n(n<=50000) 数组 arr,进行Q次查询(Q<=200000),每次查询的内容为数组arr在 [L , R] 的切片的极差(最大元素 - 最小元素)
二、解题思路
1、线段树
区间极差其实就是 区间内最大值 - 区间内最小,那么就想到RMQ,用线段树去维护一个区间内的最大和最小元素,然后根据问题的区间 L 和 R,找到相关的线段树节点,从中找出 最大值最大的,然后减去最大值 最小的即可。
实现的方式就非常简单了,因为是线段树,所以就把叶子节点的数量扩展到满足 2^i >= n_的最小i的2^i,然后给那些多扩展出来的节点的最小值设置成无穷大,最大值设置成负无穷大,则不会影响线段树计算
设一开始输入的规模为n_,然后线段树叶子节点数量为n(一定需要为2的次幂),设输入的数组为num,线段树最大值datMax,最小值为datMin,为计算叶子节点对应的数组下标,可以用 i - n + 1,其中 i 是线段树节点的下标, i - n + 1是数组的下标,对于i - n + 1
然后计算父节点的时候,那就 datMin[i]=min(datMin[i * 2 + 1] , datMin[i * 2 + 2]),datMax[i]=max(datMax[i * 2 + 1] , datMax[i * 2 + 2])即可。
然后判断是否为叶子节点,就看 i 是不是大于 n - 1即可(n不是输入的规模,而是大于输入规模n_的第一个 2^i)
构建树的时候从 i=2*n-2;i>=0;i--即可。
然后查询L R的时候,只需要从根节点开始进行如下三个步骤,可以设最终用到的最小值为mint,最大值为maxt,然后设置mint=inf,maxt=inf * (-1)
1、节点 i 的区间如果与 L 和 R 毫无关联,则return
2、节点 i 区间被 L 和 R 完全包含,则mint=min(datMin[i],mint),maxt=max(datMax[i],maxt)
3、节点 i 与区间有重合部分,但不完全包含,递归 i * 2 + 1 和 i * 2 + 2
然后输出 maxt - mint即可解题
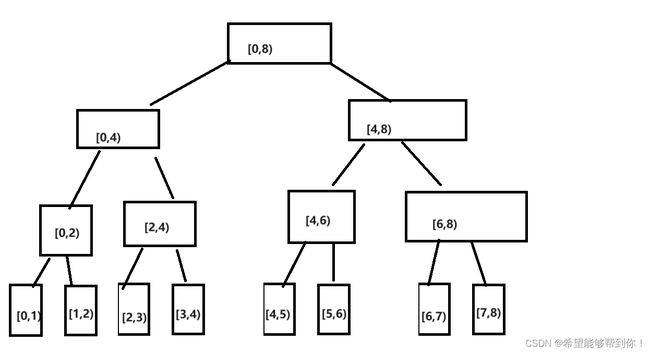
我写线段树时候,比较喜欢直接用数组,然后每个节点维护的区间为 左闭右开,比如 [0,1) [0,2) [0,4),然后我习惯于把最大区间弄成 2 的次幂,之后用无穷大和负无穷大来补充不足的值 ,之后区间通过调用方法时的参数传递,根节点 0 的区间为 [0 , n),然后如果节点 i 的区间为[L , R],则它左孩子 i * 2 + 1的区间为[0 , (L + R) / 2] ,右孩子的区间为 [(L + R) / 2, R),如果叶子节点数量时2的次幂,这个区间的计算可以通过画个图看出来 ,如下图所示。
然后另外补充一点,我觉得线段树叶子大小还是要扩充到2^i,不然叶子节点的赋值容易出问题,就是用循环方式,从2*n - 2到0用i-- 初始化的时候,一定会出问题,如下所示。
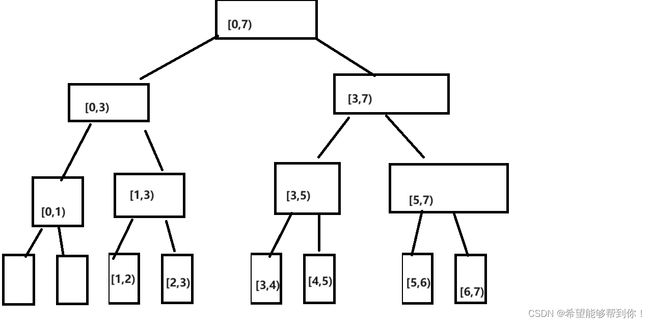
因为叶子节点不一定是下标最大的几个节点,也不一定是 i >= n - 1的节点,所以循环方式初始化有问题,但是使用递归初始化的话,不会有问题,而且代码看起来更精简。
不过还是建议把线段树的叶子节点扩充到最接近的 2的次幂,这样的话每一层的节点维护的区间是一样长的,更规范。
2、平方分割
平方分割的话,就简单很多了,我计算了下 根号 50000是 224再多一点,所以直接定义230个桶,设桶的大小为根号n下取整,定义为B,然后第 i 个桶维护的区间是 [i * B,(i + 1) * B),如果 i * B < n,但是 (i + 1) * B大于 n 时,那么桶 i 维护的区间为 [ i * B , n),然后维护每个桶的最大值和最小值。
设每个桶的最小值bucketMin,最大值为bucketMax,最开始把满足 i * B < n范围内所有的bucketMax[i]=inf*(-1),bucketMin[i]=inf,(我将区间从0开始,左闭右开,则n-1为最后一个有效位置,当i * B == n则,代表第 i 个桶的起点维护的是数组里不存在的元素,所以 i * B < n为范围)初始化的时候,只需用 i 循环 num 数组
1、bucketMax[i / B]=max(bucketMax[i / B] , num[i])
2、bucketMin[i / B]=max(bucketMin[i / B] , num[i])
然后对于每一次输入的 [L , R]区间,我们把它变成左闭右开,初始位置从0开始,即 L--,R不变,然后设置两个变量 mint = inf,maxt= inf * (-1)(inf是无穷大,定义成 0x3f3f3f3f就行)
用一个数组bucketQue记录包含在区间里的桶,设它的长度为queLen,初始化为 0
在 i * B < n 的范围内循环所有的桶,计算桶的区间左边bucketL = i * B,区间右边 bucketR = (i + 1)*B,然后bucketR > n 时,bucketR = n,如果 [bucketL , bucketR)被 [L , R)完全包含,则
1、mint = min(mint , bucketMin[i])
2、maxt = max(maxt , bucketMax[i])
3、bucketQue[queLen++] = i
然后处理不在桶内的区间,如果 queLen==0,则区间内不完整包含任何一个桶,则循环 [L , R)
1、mint = min(mint , num[i])
2、maxt = max(maxt ,num[i])
如果queLen>0,则循环 [L , bucketQue[0] * B) 和 [(bucketQue[queLen - 1] + 1) * B) , R)
1、mint = min(mint , num[i])
2、maxt = max(maxt ,num[i])
不难看出,bucketQue[0]是第一个桶,bucketQue[0] * B是第一个桶的起点(包含)
bucketQue[queLen - 1]是最后一个桶,bucketQue[queLen - 1]是最后一个桶的终点(不包含)
所以这两段左闭右开的区间是不包含在桶内的,而且在区间内的边缘,需要计算。
然后输出 maxt - mint即可。
三、代码
1、线段树(循环方式初始化,初始化叶子节点大小为 2的次幂)
#include
using namespace std;
int datTall[131080], datShort[131080], n, n_, num[50007], inf = 0x3f3f3f3f, minShort, maxTall;
void input()
{
for (int i = 0; i < n_; i++)
{
scanf("%d", &num[i]);
}
}
void init()
{
n = 1;
while (n < n_)
{
n = n * 2;
}
for (int i = (2 * n - 2); i >= 0; i--)
{
if (i >= (n - 1))
{
if ((i - n + 1) < n_)
{
datTall[i] = num[i - n + 1];
datShort[i] = num[i - n + 1];
}
else
{
datTall[i] = -inf;
datShort[i] = inf;
}
}
else
{
int lch = i * 2 + 1;
int rch = i * 2 + 2;
datTall[i] = max(datTall[lch], datTall[rch]);
datShort[i] = min(datShort[lch], datShort[rch]);
}
}
}
void query(int l_, int r_, int i, int l, int r)
{
if (l_ >= r || r_ <= l)
{
}
else if (l >= l_ && r <= r_)
{
minShort = min(minShort, datShort[i]);
maxTall = max(maxTall, datTall[i]);
}
else
{
query(l_, r_, i * 2 + 1, l, (l + r) / 2);
query(l_, r_, i * 2 + 2, (l + r) / 2, r);
}
}
int main()
{
int m, L, R;
scanf("%d%d", &n_, &m);
input();
init();
while (m--)
{
scanf("%d%d", &L, &R);
minShort = inf;
maxTall = -inf;
query(L - 1, R, 0, 0, n);
printf("%d\n", maxTall - minShort);
}
return 0;
} 2、平方分割
#include
#include
using namespace std;
int datTall[230], datShort[230], num[50007], n, B, inf = 0x3f3f3f3f, bucketQue[230], queLen;
void input()
{
B = 1;
while (B * B <= n)
{
B++;
}
B--;
for (int i = 0; (i * B) < n; i++)
{
datTall[i] = -inf;
datShort[i] = inf;
}
for (int i = 0; i < n; i++)
{
scanf("%d", &num[i]);
datTall[i / B] = max(datTall[i / B], num[i]);
datShort[i / B] = min(datShort[i / B], num[i]);
}
}
void solve(int L, int R)
{
queLen = 0;
int minTall = inf, maxTall = -inf;
for (int i = 0; (i * B) < n; i++)
{
int bucketL = i * B;
int bucketR = (i + 1) * B;
bucketR = (bucketR > n ? n : bucketR);
if (bucketL >= L && bucketR <= R)
{
bucketQue[queLen++] = i;
minTall = min(minTall, datShort[i]);
maxTall = max(maxTall, datTall[i]);
}
}
if (queLen == 0)
{
for (int i = L; i < R; i++)
{
minTall = min(minTall, num[i]);
maxTall = max(maxTall, num[i]);
}
}
else
{
for (int i = L; i < (bucketQue[0] * B); i++)
{
minTall = min(minTall, num[i]);
maxTall = max(maxTall, num[i]);
}
for (int i = ((bucketQue[queLen - 1] + 1) * B); i < R; i++)
{
minTall = min(minTall, num[i]);
maxTall = max(maxTall, num[i]);
}
}
printf("%d\n", maxTall - minTall);
}
int main()
{
int m, L, R;
scanf("%d%d", &n, &m);
input();
while (m--)
{
scanf("%d%d", &L, &R);
solve(L - 1, R);
}
return 0;
} 3、线段树(递归方式初始化,非完美二叉树,代码简洁)
#include
using namespace std;
int datShort[131080], datTall[131080], n, num[50009], inf = 0x3f3f3f3f, mint, maxt;
void input()
{
for (int i = 0; i < n; i++)
{
scanf("%d", &num[i]);
}
}
void build(int i, int l, int r)
{
if (r - l == 1)
{
datShort[i] = num[l];
datTall[i] = num[l];
}
else
{
int lch = i * 2 + 1;
int rch = i * 2 + 2;
build(lch, l, (l + r) / 2);
build(rch, (l + r) / 2, r);
datShort[i] = min(datShort[lch], datShort[rch]);
datTall[i] = max(datTall[lch], datTall[rch]);
}
}
void query(int l_, int r_, int i, int l, int r)
{
if (l_ >= r || r_ <= l)
{
}
else if (l >= l_ && r <= r_)
{
mint = min(mint, datShort[i]);
maxt = max(maxt, datTall[i]);
}
else
{
query(l_, r_, i * 2 + 1, l, (l + r) / 2);
query(l_, r_, i * 2 + 2, (l + r) / 2, r);
}
}
int main()
{
int m, L, R;
scanf("%d%d", &n, &m);
input();
build(0, 0, n);
while (m--)
{
scanf("%d%d", &L, &R);
mint = inf, maxt = -inf;
query(L - 1, R, 0, 0, n);
printf("%d\n", maxt - mint);
}
return 0;
}