Redis底层核心数据结构详解
文章目录
- 一、深入String(SDS)
-
- 1. 字符串简介
- 2. SDS存在的意义
- 3. SDS结构设计
- 4. SDS与C字符串的区别
-
- 4.1 常数复杂度获取字符串长度
- 4.2 杜绝缓冲区溢出
- 4.3 二进制安全
- 4.4 SDS API
- 5 小结
- 二、深入List (QuickList)
-
- 1. 链表节点结构设计
- 2. Redis的链表实现的优点
- 3. Redis的链表的缺陷
- 4. 压缩列表
-
- 4.1 连锁更新
- 4.2 压缩链表的缺陷
- 4.3 Quicklist
-
- 4.3.1 quicklist结构设计
- 5. 链表和链表节点的API
- 三、深入Hash (ListPack)
-
- 1. 哈希表结构设计
- 2. 哈希冲突
-
- 2.1 什么是哈希冲突
- 2.2 链式哈希
- 2.3 rehash
-
- 2.3.1 渐进式 rehash
- 2.3.2 rehash 触发条件
- 3. listpack 结构设计
- 四、深入Set (整数集合)
-
- 1. 整数集合结构设计
- 2. 整数集合的升级操作
- 3. 整数集合升级有什么好处呢?
- 4. 整数集合支持降级操作吗?
- 五、深入Zset (SkipList)
-
- 1. 跳表结构设计
- 2. 跳表节点查询过程
- 3. 跳表节点层数设置
一、深入String(SDS)
1. 字符串简介
字符串在 Redis 中是很常用的,键值对中的键是字符串类型,值有时也是字符串类型。
Redis 是用 C 语言实现的,但是它没有直接使用 C 语言的 char* 字符数组来实现字符串,而是自己封装了一个名为简单动态字符串 (simple dynamic string,SDS) 的数据结构来表示字符,也就是 Redis 的 String 数据类型的底层数据结构是 SDS
2. SDS存在的意义
Redis设计了SDS(Simple Dynamic String)结构来表示字符串,主要是为了弥补C语言的字符数组(char*)存在的一些缺陷。
- 获取字符串长度的时间复杂度为 O (N)
- 字符串的结尾是以 “\0” 字符标识,字符串里面不能包含有 ’ \0 ’ 字符,因此不能保存二进制数据
- 字符串操作函数不高效目不安全,比如有缓冲区溢出的风险,有可能会造成程序运行终止
3. SDS结构设计
- free 属性的值为0,表示这个 SDS 没有分配任何未使用空间。
- len 属性的值为 5,表示这个 SDS 保存了一个五字节长的字符串。
- buf 属性是一个char类型的数组,数组的前五个字节分别保存了,’ R ‘、’ e ‘、’ d ’ 、’ i ‘、’ s ’ 五个字符,而最后一个字节则保存了空字符 ’ \0 '。
4. SDS与C字符串的区别
4.1 常数复杂度获取字符串长度
- 因为 C 字符串并不记录自身的长度信息,所以为了获取一个 C字符串的长度,程序必须遍历整个字符串,对遇到的每个字符进行计数,直到遇到代表字符串结尾的空字符为止,这个操作的复杂度为 O(N)
- 和 C 字符串不同,因为 SDS在 len 属性中记录了SDS 本身的长度,所以获取一个 SDS 长度的复杂度仅为 O(1)
4.2 杜绝缓冲区溢出
- 除了获取字符串长度的复杂度高之外,C 字符串不记录自身长度带来的另一个问题是容易造成缓冲区溢出(buffer overflow)。
- 与 C 字符串不同,SDS 的空间分配策略完全杜绝了发生缓冲区溢出的可能性:
- 当 SDS API需要对 SDS 进行修改时,API会先检查SDS 的空间是否满足修改所需的要求,如果不满足的话,API会自动将 SDS 的空间扩展至执行修改所需的大小,然后才执行实际的修改操作,所以使用 SDS 既不需要手动修改 SDS 的空间大小,也不会出现前面所说的缓冲区溢出问题。
4.3 二进制安全
- 因为 SDS 不需要用 ’ \0 ’ 字符来标识字符串结尾了,而是有个专门的 len 成员变量来记录长度,所以可存储包含 ’ \0’ 的数据。但是 SDS 为了兼容部分 C 语言标准库的函数,SDS 字符串结尾还是会加上 ’ \0 ’ 字符
- 因此,SDS 的 API 都是以处理二进制的方式来处理 SDS 存放在 bufl 里的数据,程序不会对其中的数据做任何限制,数据写入的时候时什么样的,它被读取时就是什么样的。
- 通过使用二进制安全的 SDS,而不是 C 字符串,使得 Redis 不仅可以保存文本数据,也可以保存任意格式的二进制数据。
4.4 SDS API
下图列出了SDS的主要操作API:
5 小结
下图对C字符串和 SDS之间的区别进行了总结:
二、深入List (QuickList)
Redis 的 List 对象的底层实现之一就是链表。C 语言本身没有链表这个数据结构的,所以 Redis 自己设计了一个链
表数据结构。
1. 链表节点结构设计
先来看看 [链表节点] 结构的样子:
typedef struct listNode {
struct listNode *prev;
struct listNode *next;
void *value;
} listNode;
有前置节点和后置节点,可以看的出,这个是一个双向链表

不过,Redis在 listNode 结构体基础上又封装了 list 这个数据结构,这样操作起来会更方便,链表结构如下:
typedef struct list {
listNode *head;
listNode *tail;
void *(*dup)(void *ptr);
void (*free)(void *ptr);
int (*match)(void *ptr, void *key);
unsigned long len;
} list;
list 结构为链表提供了链表头指针 head、链表尾节点 tail、链表节点数量 len、以及可以自定义实现的 dup、free、match 函数
- dup 函数用于复制链表节点所保存的值;
- free 函数用于释放链表节点所保存的值;
- match 函数则用于对比链表节点所保存的值和另一个输人值是否相等
下图是由一个list结构和三个listnode 结构组成的链表。

2. Redis的链表实现的优点
- 双端:链表节点带有 prev和next 指针,获取某个节点的前置节点和后置节点的复杂度都是 O(1)。
- 无环:表头节点的prev指针和表尾节点的next 指针都指向 NULL,对链表的访问以NULL为终点。
- 带表头指针和表尾指针:通过 list 结构的 head 指针和 tail 指针,序获取链表的表头节点和表尾节点的复杂度为 (O1)。
- 带链表长度计数器:程序使用 list 结构的 len 属性来对 list 持有的链表节点进行计数,程序获取链表中节点数量的复杂度为 O(1)。
- 多态:链表节点使用 void* 指针来保存节点值,并且可以通过 list 结构的 dup、free、match 三个属性为节点值设置类型特定函数,所以链表可以用于保存各种不同类型的值。
3. Redis的链表的缺陷
- 链表每个节点之间的内存都是不连续的,意味着无法很好利用 CPU 缓存。能很好利用 CPU 缓存的数据结构就是数组,因为数组的内存是连续的,这样就可以充分利用 CPU 缓存来加速访问。
- 还有一点,保存一个链表节点的值都需要一个链表节点结构头的分配,内存开销较大。因此,Redis 3.0 的 List 对象在数据量比较少的情况下,会采用[压缩列表,作为底层数据结构的实现,它的优势是节省内存空间,并且是内存紧凑型的数据结构。
- 不过,压缩列表存在性能问题(具体什么问题,下面会说),所以 Redis 在 3.2 版本设计了新的数据结构 quicklist ,并将 List 对象的底层数据结构改由 quicklist 实现。
- 然后在 Redis 5.0 设计了新的数据结构 listpack,沿用了压缩列表紧凑型的内存布局,最终在最新的 Redis 版本将 Hash 对象和 Zset 对象的底层数据结构实现之一的压缩列表,替换成由 listpack 实现。
4. 压缩列表
- 压缩列表的最大特点,就是它被设计成一种内存紧凑型的数据结构,占用一块连续的内存空间,不仅可以利用CPU 缓存,而且会针对不同长度的数据,进行相应编码,这种方法可以有效地节省内存开销。
- 但是,压缩列表的缺陷也是有的:不能保存过多的元素,否则查询效率就会降低,新增或修改某个元素时,压缩列表占用的内存空间需要重新分配,甚至可能引发连锁更新的问题。
- 因此,Redis 对象 (List 对象、Hash 对象、Zset 对象)包含的元素数量较少,或者元素值不大的情况才会使用压缩列表作为底层数据结构。

压缩列表在表头有三个字段:
- zlbytes,记录整个压缩列表占用对内存字节数;
- zltail,记录压缩列表[尾部,节点距离起始地址由多少字节,也就是列表尾的偏移量
- zllen,记录压缩列表包含的节点数量;
末尾也有一个字段:
- zlend,标记压缩列表的结束点,固定值 0xFF (+进制255)
在压缩列表中,如果我们要查找定位第一个元素和最后一个元素,可以通过表头三个字段的长度直接定位,复杂度是 0(1)。而查找其他元素时,就没有这么高效了,只能逐个查找,此时的复杂度就是 O(N)了,因此压缩列表不适
合保存过多的元素
另外,压缩列表节点 (entry) 的构成如下:

压缩列表节点包含三部分内容
- prevlen,记录了 [ 前一个节点 ] 的长度
- encoding,记录了当前节点实际数据的类型以及长度
- data,记录了当前节点的实际数据
当我们往压缩列表中插入数据时,压缩列表就会根据数据是字符串还是整数,以及数据的大小,会使用不同空间大小的 prevlen 和 encoding 这两个元素里保存的信息,这种根据数据大小和类型进行不同的空间大小分配的设计思想,正是 Redis 为了节省内存而采用的。
分别说下,prevlen 和 encoding 是如何根据数据的大小和类型来进行不同的空间大小分配。
压缩列表里的每个节点中的 prevlen 属性都记录了[前一个节点的长度,而且 prevlen 属性的空间大小跟前一个节点长度值有关,比如:
- 如果前一个节点的长度小于 254 字节,那么 prevlen 属性需要用 1 字节的空间来保存这个长度值;
- 如果前一个节点的长度大于等于 254 字节,那么 prevlen 属性需要用 5 字节的空间来保存这个长度值;
encoding 属性的空间大小跟数据是字符串还是整数,以及字符串的长度有关:
- 如果当前节点的数据是整数,则 encoding 会使用 1 字节的空间进行编码。
- 如果当前节点的数据是字符串,根据字符串的长度大小,encoding 会使用 1 字节/2字节/5字节的空间进行编码。
4.1 连锁更新
压缩列表除了查找复杂度高的问题,还有一个问题。
压缩列表新增某个元素或修改某个元素时,如果空间不不够,压缩列表占用的内存空间就需要重新分配。而当新插入的元素较大时,可能会导致后续元素的 prevlen 占用空间都发生变化,从而引起连锁更新,问题,导致每个元素的空间都要重新分配,造成访问压缩列表性能的下降。
前面提到,压缩列表节点的 prevlen 属性会根据前一个节点的长度进行不同的空间大小分配:
- 如果前一个节点的长度小于 254 字节,那么 prevlen 属性需要用 1 字节的空间来保存这个长度值
- 如果前一个节点的长度大于等于 254 字节,那么 prevlen 属性需要用 5 字节的空间来保存这个长度值
现在假设一个压缩列表中有多个连续的、长度在 250~ 253 之间的节点,如下图:

因为这些节点长度值小于 254 字节,所以 prevlen 属性需要用 1 字节的空间来保存这个长度值。
这时,如果将一个长度大于等于 254 字节的新节点加入到压缩列表的表头节点,即新节点将成为 entry1 的前置节点如下图:

因为 e1 节点的 prevlen 属性只有 1 个字节大小,无法保存新节点的长度,此时就需要对压缩列表的空间重分配操作,并将 e1 节点的 prevlen 属性从原来的 1 字节大小扩展为 5 字节大小。
多米诺牌的效应就此开始。

entry1 原本的长度在 250~253 之间,因为刚才的扩展空间,此时 entry1 的长度就大于等于 25 了,因此原本 entry2 保存e1的 prevlen 属性也必须从 1 字节扩展至 5 字节大小。
正如扩展 entry1 引发了对 entry12 扩展一样,扩展 entry2 也会引发对 entry3 的扩展,而扩展 entry4 又会引发对 eentry5的扩展…一直持续到结尾。
这种在特殊情况下产生的连续多次空间扩展操作就叫做[连锁更新],就像多米诺牌的效应一样,第一张牌倒下了,推动了第二张牌倒下,第二张牌倒下,又推动了第三张牌倒下…
4.2 压缩链表的缺陷
空间扩展操作也就是重新分配内存,因此连锁更新一旦发生,就会导致压缩列表占用的内存空间要多次重新分配这就会直接影响到压缩列表的访问性能。
所以说,虽然压缩列表紧凑型的内存布局能节省内存开销,但是如果保存的元素数量增加了,或是元素变大了,会导致内存重新分配,最糟糕的是会有[连锁更新]的问题。
因此,压缩列表只会用于保存的节点数量不多的场景,只要节点数量足够小,即使发生连锁更新,也是能接受的
虽说如此,Redis 针对压缩列表在设计上的不足,在后来的版本中,新增设计了两种数据结构:
quicklist (Redis3.2 引入) 和 listpack (Redis 5.0 引入)。这两种数据结构的设计目标,就是尽可能地保持压缩列表节省内存的优势,同时解决压缩列表的 [连锁更新] 的问题。
4.3 Quicklist
在 Redis 3.0 之前,List 对象的底层数据结构是双向链表或者压缩列表。然后在 Redis 3.2 的时候,List 对象的底层改由 quicklist 数据结构实现。
其实 quicklist 就是[双向链表 + 压缩列表] 组合,因为一个 guicklist 就是一个链表,而链表中的每个元素又是个压缩列表。
在前面将压缩列表的时候,也提到了压缩列表的不足,虽然缩列表是通过紧凑型的内存布局节省了内存开销但是因为它的结构设计,如果保存的元素数量增加,或者元素变大了,压缩列表会有,连锁更新,的风险,一旦发生,会造成性能下降.
quicklist 解决办法,通过控制每个链表节点中的压缩列表的大小或者元素个数,来规避连锁更新的问题。因为压缩列表元素越少或越小,连锁更新带来的影响就越小,从而提供了更好的访问性能。
4.3.1 quicklist结构设计
quicklist 的结构体跟链表的结构体类似,都包含了表头和表尾,区别在于 quicklist 的节点是quicklistNode。
typedef struct quicklist {
quicklistNode *head;
quicklistNode *tail;
unsigned long count; /* total count of all entries in all ziplists */
unsigned long len; /* number of quicklistNodes */
} quicklist;
接下来看看,quicklistNode 的结构定义:
typedef struct quicklistNode {
struct quicklistNode *prev;
struct quicklistNode *next;
unsigned char *zl; /*quicklistNode指向的压缩列表*/
unsigned int sz; /* ziplist size in bytes */
unsigned int count : 16; /* count of items in ziplist */
......
} quicklistNode;
可以看到,quicklistNode 结构体里包含了前一个节点和下一个节点指针,这样每个 quicklistNode 形成了一个双向链表。但是链表节点的元素不再是单纯保存元素值,而是保存了一个压缩列表,所以 quicklistNode 结构体里有个指向压缩列表的指针。

在向 quicklist 添加一个元素的时候,不会像普通的链表那样,直接新建一个链表节点。而是会检查插入位置的压缩列表是否能容纳该元素,如果能容纳就直接保存到 quicklistNode 结构里的压缩列表,如果不能容纳,才会新建个新的 quicklistNode 结构。
quicklist 会控制 quicklistNode 结构里的压缩列表的大小或者元素人数,来规避潜在的连锁更新的风险(但是这并没有完全解决连锁更新的问题)。
5. 链表和链表节点的API
三、深入Hash (ListPack)
哈希表是一种保存键值对 (key-value)的数据结构
哈希表中的每一个 key 都是独一无二的,程序可以根据 key 查找到与之关联的 value,或者通过 key 来更新value,又或者根据 key 来删除整个 key-value等等。
在讲压缩列表的时候,提到过 Redis 的 Hash 对象的底层实现之一是压缩列表(最新 Redis 代码已将压缩列表替换成 listpack)。Hash 对象的另外一个底层实现就是哈希表。
哈希表优点在于,它能以 0(1)的复杂度快速查询数据。怎么做到的呢? 将 key 通过 Hash 函数的计算,就能定位数据在表中的位置,因为哈希表实际上是数组,所以可以通过索引值快速查询到数据。
但是存在的风险也是有,在哈希表大小固定的情况下,随着数据不断增多,那么哈希冲突的可能性也会越高。解决哈希冲突的方式,有很多种。
Redis 采用了[链式哈希来解决哈希冲突,在不扩容哈希表的前提下,将具有相同哈希值的数据串起来,形成链接起,以便这些数据在表中仍然可以被查询到。
1. 哈希表结构设计
Redis 的哈希表结构如下:
typedef struct dictht {
dictEntry **table;
unsigned long size; // hashtable 容量
unsigned long sizemask; // size -1
unsigned long used; // hashtable 元素个数 used / size =1
} dictht;
可以看到,哈希表是一个数组 (dictEntry **table) ,数组的每个元素是一个指向[哈希表节点 (dictEntry)]的
指针。

哈希表节点的结构如下:
typedef struct dictEntry {
void *key; //键
union { //值
void *val;
uint64_t u64;
int64_t s64;
double d;
} v;
struct dictEntry *next; //形成链表
} dictEntry;
dictEntry 结构里不仅包含指向键和值的指针,还包含了指向下一个哈希表节点的指针,这个指针可以将多个哈希值相同的键值对链接起来,以此来解决哈希冲突的问题,这就是链式哈希。
另外,dictEntry 结构里键值对中的值是一个[联合体定义的,因此,键值对中的值可以是一个指向实际值的指针,或者是一个无符号的 64 位整数或有符号的 64 位整数或double 类的值。
这么做的好处是可以节省内存空间,因为当值]是整数或浮点数时,就可以将值的数据内嵌在 dictEntry 结构里,无需再用一个指针指向实际的值,从而节省了内存空间。
2. 哈希冲突
哈希表实际上是一个数组,数组里多每一个元素就是一个哈希桶。
当一个键值对的键经过 Hash 函数计算后得到哈希值,再将(哈希值 % 哈希表大小) 取模计算,得到的结果值就是该 key-value 对应的数组元素位置,也就是第几个哈希桶。
2.1 什么是哈希冲突
- 举个例子,有一个可以存放 8 个哈希桶的哈希表。key1 经过哈希函数计算后,再将[哈希值 % 8] 进行取模算,结果值为 1,那么就对应哈希桶 1,类似的,key9 和 key10 分别对应哈希桶 1 和桶 6。
- 哈希表中同一个哈希桶上时,此时称这些 key 发生了冲突
此时,key1 和 key9 对应到了相同的哈希桶中,这就发生了哈希冲突。因此,当有两个以上数量的 kay 被分配到了
2.2 链式哈希
Redis 采用了[链式哈希]的方法来解决哈希冲突。
实现的方式就是每个哈希表节点都有一个 next 指针,用于指向下一个哈希表节点,因此多个哈希表节点可以用next 指针构成一个单项链表,被分配到同一个哈希桶上的多个节点可以用这个单项链表连接起来,这样就解决了哈希冲突。
还是用前面的哈希冲突例子,key1 和 key9 经过哈希计算后,都落在同一个哈希桶,链式哈希的话,key1 就会通过 next 指针指向 key9,形成一个单向链表。不过,链式哈希局限性也很明显,随着链表长度的增加,在查询这一位置上的数据的耗时就会增加,毕竟链表的查询的时间复杂度是 O(n)。
要想解决这一问题,就需要进行 rehash,也就是对哈希表的大小进行扩展。接下来,看看 Redis 是如何实现的rehash 的。
2.3 rehash
哈希表结构设计的这一小节,介绍了 Redis 使用 dictht 结构体表示哈希表。不过,在实际使用哈希表时Redis 定义一个 dict 结构体,这个结构体里定义了两个哈希表 (ht[2]) 。
typedef struct dict {
dictType *type;
void *privdata;
dictht ht[2];// ht[0] , ht[1] =null
long rehashidx; /* rehashing not in progress if rehashidx == -1 */
unsigned long iterators; /* number of iterators currently running */
} dict;
之所以定义了 2 个哈希表,是因为进行 rehash 的时候,需要用上 2 个哈希表了。

在正常服务请求阶段,插入的数据,都会写入到[哈希表 1 ,此时的哈希表 2并没有被分配空间。
随着数据逐步增多,触发了 rehash 操作,这个过程分为三步:
- 给[哈希表 2] 分配空间,一般会比[哈希表 1] 大 2 倍;
- 将[哈希表 1]的数据迁移到[哈希表 2] 中;
- 迁移完成后,[哈希表 1] 的空间会被释放,并把哈希表 2 设置为哈希表 1,然后在哈希表 2新创建一个空白的哈希表,为下次 rehash 做准备。
这个过程看起来简单,但是其实第二步很有问题,如果 哈希表1的数据量非常大,那么在迁移至哈希表2的时候,因为会涉及大量的数据拷贝,此时可能会对 Redis 造成阻塞,无法服务其他请求。
2.3.1 渐进式 rehash
为了避免 rehash 在数据迁移过程中,因拷贝数据的耗时,影响 Redis 性能的情况,所以 Redis 采用了渐进式rehash,也就是将数据的迁移的工作不再是一次性迁移完成,而是分多次迁移。
渐进式 rehash 步骤如下:
-
给 [哈希表2] 分配空间。
-
在 rehash 进行期间,每次哈希表元素进行新增、删除、查找或者更新操作时,Redis 除了会执行对应的操作之外,还会顺序将[哈希表 1] 中索引位置上的所有 key-value 迁移到[哈希表 2] 上;
-
随着处理客户端发起的哈希表操作请求数量越多,最终在某个时间点,会把[哈希表 1] 的所有 key-value 移到[哈希表 2,从而完成rehash 操作。这样就巧妙地把一次性大量数据迁移工作的开销,分摊到了多次处理请求的过程中,避免了一次性 rehash 的耗时操作
在进行渐进式 rehash 的过程中,会有两个哈希表,所以在渐进式 rehash 进行期间,哈希表元素的删除、查找、更新等操作都会在这两个哈希表进行。
比如,查找一个 key 的值的话,先会在哈希表 1 里面进行查找,如果没找到,就会继续到哈希表 2 里面进行找到。
另外,在渐进式 rehash 进行期间,新增一个 key-value 时,会被保存到 哈希表 2 里面,而哈希表 1 则不再进行任何添加操作,这样保证了[哈希表 1]的 key-value 数量只会减少,随着 rehash 操作的完成,最终哈希表 1 就会变成空表。
2.3.2 rehash 触发条件
rehash 的触发条件跟负载因子 (load factor) 有关系。负载因子可以通过下面这个公式计算:

触发 rehash 操作的条件,主要有两个:
- 也就是没有执行 RDB 快照当负载因子大于等于 1,并且 Redis 没有在执行 bgsave 命令或者 bgrewiteaof 命令,或没有进行 AOF 重写的时候,就会进行 rehash 操作。
- 当负载因子大于等于 5时,此时说明哈希冲突非常严重了,不管有没有有在执行 RDB 快照或 AOF 重写,都会强制进行 rehash 操作。
在 Redis 5.0 设计了新的数据结构 listpack,沿用了压缩列表紧凑型的内存布局,最终在最新的 Redis 版本,将Hash 对象和 Zset 对象的底层数据结构实现之一的压缩列表,替换成由 listpack 实现。
3. listpack 结构设计
listpack 采用了压缩列表的很多优秀的设计,比如还是用一块连续的内存空间来紧凑地保存数据,并且为了节省内存的开销,listpack 节点会采用不同的编码方式保存不同大小的数据。
先来看看 listpack 结构:

istpack 头包含两个属性,分别记录了 listpack 总字节数和元素数量,然后 listpack 末尾也有个结尾标识。图中的listpack entry 就是 listpack 的节点了。
每个 listpack 节点结构如下:

主要包含三个方面内容:
- encoding,定义该元素的编码类型,会对不同长度的整数和字符串进行编码
- data,实际存放的数据
- len,encoding+data的总长度
可以看到,listpack 没有像压缩列表中记录前一个节点长度的字段了,listpack 只记录当前节点的长度,当我们向listpack 中加入一个新元素的时候,不会影响其他节点的长度字段的变化,从而避免了压缩列表的连锁更新问题。
四、深入Set (整数集合)
整数集合是 Set 对象的底层实现之一。当一个 Set 对象只包含整数值元素,并且元素数量小于 set-max-intset-entries参数默认的512时,就会使用整数集这个数据结构作为底层实现,否则会使用hash表的方式实现。
1. 整数集合结构设计
typedef struct intset {
//编码方式
uint32_t encoding;
//集合中包含的元素数量
uint32_t length;
//保存元素的数组
int8_t contents[];
} intset;
可以看到,保存元素的容器是一个 contents 数组,虽然 contents 被声明为 int8 t 类型的数组,但是实际上contents 数组并不保存任何 int8 t 类型的元素,contents 数组的真正类型取决于 intset 结构体里的 encoding 属性的值。
比如:
- 如果 encoding 属性值为 INTSET_ENC INT16,那么 contents 就是一个int16_t 类型的数组,数组中每一个元素的类型都是 int16_t;
- 如果 encoding 属性值为 INTSET_ENC INT32,那么 contents 就是一个int32_t 类型的数组,数组中每一个元素的类型都是 int32_t;
- 如果 encoding 属性值为 INTSET_ENC INT64,那么 contents 就是一个 int64_t 类型的数组,数组中每一个元素的类型都是 int64_t;
不同类型的 contents 数组,意味着数组的大小也会不同。
2. 整数集合的升级操作
-
整数集合会有一个升级规则,就是当我们将一个新元素加入到整数集合里面,如果新元素的类型 (int32_t)比整数集合现有所有元素的类型 (int16_t)都要长时,整数集合需要先进行升级,也就是按新元素的类型 (int32_t)扩展 contents 数组的空间大小,然后才能将新元素加入到整数集合里,当然升级的过程中,也要维持整数集合的有序性。
-
整数集合升级的过程不会重新分配一个新类型的数组,而是在原本的数组上扩展空间,然后在将每个元素按间隔类型大小分割,如果 encoding 属性值为 INTSET ENC INT16,则每个元素的间隔就是 16 位

现在,往这个整数集合中加入一个新元素 65535,这个新元素需要用 int32_t 类型来保存,所以整数集合要进行升级操作,首先需要为 contents 数组扩容,在原本空间的大小之上再扩容多 80 位(4x32-3x16=80),这样就能保存下 4 个类型为 int32 t 的元素。

扩容完 contents 数组空间大小后,需要将之前的三个元素转换为 int32 t 类型,并将转换后的元素放置到正确的位上面,并且需要维持底层数组的有序性不变,整个转换过程如下:

3. 整数集合升级有什么好处呢?
如果要让一个数组同时保存 int16 t、int32 t、int64 t类型的元素,最简单做法就是直接使用 int64 t 类型的数组。不过这样的话,当如果元素都是 int16 t 类型的,就会造成内存浪费的情况。
整数集合升级就能避免这种情况,如果一直向整数集合添加 int16t 类型的元素,那么整数集合的底层实现就一直是用 int16t类型的数组,只有在我们要将 nt32t 类型或 int64 t 类型的元素添加到集合时,才会对数组进行升级操作。因此,整数集合升级的好处是节省内存资源。
4. 整数集合支持降级操作吗?
不支持降级操作,一旦对数组进行了升级,就会一直保持升级后的状态。比如前面的升级操作的例子,如果删除了65535 元素,整数集合的数组还是 int32 t 类型的,并不会因此降级为 int16_t 类型。
五、深入Zset (SkipList)
Redis 只有在 Zset 对象的底层实现用到了跳表,跳表的优势是能支持平均 0(logN)复杂度的节点查找,用空间换时间。
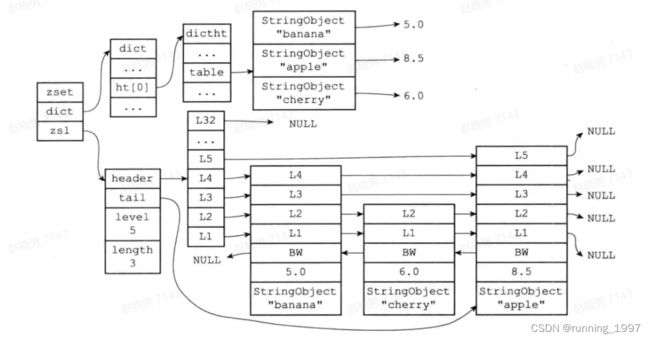
Zset 对象是唯一一个同时使用了两个数据结构来实现的 Redis 对象,这两个数据结构一个是跳表,一个是哈希表,这样的好外是既能进行高效的范围查询,也能进行高效单点查询。
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;
Zset 对象能支持范围查询(如 ZRANGEBYSCORE 操作),这是因为它的数据结构设计采用了跳表,而又能以常数
复杂度获取元素权重 (如 ZSCORE 操作),这是因为它同时采用了哈希表进行索引。
ZADD price 8.5 apple 5.0 banana 6.0 cherry
1. 跳表结构设计
链表在查找元素的时候,因为需要逐一查找,所以查询效率非常低,时间复杂度是O(N),于是就出现了跳表。跳表是在链表基础上改进过来的,实现了一种 多层的有序链表 ,这样的好处是能快读定位数据。
那跳表长什么样呢?
下面举个例子,下图展示了一个层级为 3 的跳表:

图中头节点有 L0 ~ L2 三个头指针,分别指向了不同层级的节点,然后每个层级的节点都通过指针连接起来。
- L0 层级共有 5 个节点,分别是节点1、2、3、4、5;
- L1 层级共有 3 个节点,分别是节点 2、3、5;
- L2 层级只有 1 个节点,也就是节点 3。
如果我们要在链表中查找节点 4 这个元素,只能从头开始遍历链表,需要查找 4 次,而使用了跳表后,只需要查找 2次就能定位到节点 4,因为可以在头节点直接从 L2 层级跳到节点 3,然后再往前遍历找到节点 4。
可以看到,这个查找过程就是在多个层级上跳来跳去,最后定位到元素。当数据量很大时,跳表的查找复杂度就是0(logN)。
那跳表节点是怎么实现多层级的呢? 这就需要看 [跳表节点] 的数据结构了,如下:
typedef struct zskiplistNode {
//zset对象的元素值
sds ele;
//元素权重值
double score;
//后向指针
struct zskiplistNode *backward;
// 节点的Level数组,保存每层上的前向指针和跨度
struct zskiplistLevel {
struct zskiplistNode *forward;
unsigned long span;
} level[];
} zskiplistNode;
Zset 对象要同时保存元素和元素的权重,对应到跳表节点结构里就是 sds 类型的 ele 变量和 double 类型的 score变量。每个跳表节点都有一个后向指针backward,指向前一个节点,目的是为了方便从跳表的尾节点开始访问节点,这样倒序查找时很方便。
跳表是一个带有层级关系的链表,而且每一层级可以包含多个节点,每一个节点通过指针连接起来,实现这一特性就是靠跳表节点结构体中的zskiplistLevel 结构体类型的 level 数组。
level 数组中的每一个元素代表跳表的一层,也就是由 skiplistLevel 结构体表示,比如 leve[0] 就表示第一层eve[1]就表示第二层。zskiplistLevel 结构体里定义了指向下一个跳表节点的指针]和[跨度],跨度时用来记录两个节点之间的距离。
比如,下面这张图,展示了各个节点的跨度:

第一眼看到跨度的时候,以为是遍历操作有关,实际上并没有任何关系,遍历操作只需要用前向指针就可以完成。
跨度实际上是为了计算这个节点在跳表中的排位。具体怎么做的呢? 因为跳表中的节点都是按序排列的,那么计算某个节点排位的时候,从头节点点到该结点的查询路径上,将沿途访问过的所有层的跨度累加起来,得到的结果就是目标节点在跳表中的排位。
举个例子,查找图中节点 3 在跳表中的排位,从头节点开始查找节点 3,查找的过程只经过了一个层(L3),并且层的跨度是 3,所以节点 3 在跳表中的排位是 3。
另外,图中的头节点其实也是 zskiplistNode 跳表节点,只不过头节点的后向指针、权重、元素值都会被用到,所以图中省略了这部分。
问题来了,由谁定义哪个跳表节点是头节点呢? 这就 [ 跳表 ] 结构体了,如下所示:
typedef struct zskiplist {
struct zskiplistNode *header, *tail;
unsigned long length;
int level;
} zskiplist;
跳表结构里包含了
- 跳表的头尾节点,便于在O(1)时间复杂度内访问跳表的头节点和尾节点
- 跳表的长度,便于在O(1)时间复杂度获取跳表节点的数量
- 跳表的最大层数,便于在0(1)时间复杂度获取跳表中层高最大的那个节点的层数量
2. 跳表节点查询过程
查找一个跳表节点的过程时,跳表会从头节点的最高层开始,逐一遍历每一层。在遍历某一层的跳表节点时,会用跳表节点中的 SDS 类型的元素和元素的权重来进行判断,共有两个判断条件:
-
如果当前节点的权重 [小于] 要查找的权重时,跳表就会访问该层上的下一个节点。
-
如果当前节点的权重,[等于] 要查找的权重时,并且当前节点的 SDS 类型数据 [小于] 要查找的数据时,跳表就会访问该层上的下一个节点。
-
如果上面两个条件都不满足,或者下一个节点为空时,跳表就会使用目前遍历到的节点的 level 数组里的下一层指然后沿着下一层指针继续查找,这就相当于跳到了下一层接着查找。
举个例子,下图有个 3 层级的跳表。

如果要查找 [ 元素: abcd,权重: 4 ] 的节点,查找的过程是这样的:
- 先从头节点的最高层开始,L2 指向了[ 元素: abc,权重:3 ] 节点,这节点的权重比要查找节点的小,所以要访问该层上的下一个节点。
- 但是该层上的下一个节点是空节点,于是就会跳到[ 元素: abc,权重: 3 ] 节点的下一层找,也就是 leve[1]。
- [元素: abc,权重: 3] 节点的 leve[1] 的下一个指针指向了 [ 元素: abcde,权重: 4 ] 的节点,然后将其和要查找的节点比较。虽然 [ 元素: abcde,权重: 4 ] 的节点的权重和要查找的权重相同,但是当前节点的 SDS 类型数据 [大于] 要查找的数据,所以会继续跳到[元素: bc,权重: 3] 节点的下一层去找,也就是 leve[0]。
- [ 元素: abc,权重: 3 ]节点的 leve[0] 的下一个指针指向了[元素: bcd,权重: 4 ]的节点,该节点正是要查
找的节点,查询结束。
3. 跳表节点层数设置
注意是redis5的版本
跳表的相邻两层的节点数量的比例会影响跳表的查询性能。
举个例子,下图的跳表,第二层的节点数量只有 1 个,而第一层的节点数量有 6 个。
这时,如果想要查询节点 6,那基本就跟链表的查询复杂度一样,就需要在第一层的节点中依次顺序查找,复杂度就是 O(N)了。所以,为了降低查询复杂度,我们就需要维持相邻层结点数间的关系。
跳表的相邻两层的节点数量最理想的比例是 2:1,查找复杂度可以降低到 o(logN)。
下图的跳表就是,相邻两层的节点数量的比例是 2 : 1
那怎样才能维持相邻两层的节点数量的比例为 2:1 呢?
如果采用新增节点或者删除节点时,来调整跳表节点以维持比例的方法的话,会带来额外的开销。
Redis 则采用一种巧妙的方法是,跳表在创建节点的时候,随机生成每个节点的层数,并没有严格维持相邻两层的节点数量比例为 2:1 的情况。
具体的做法是,跳表在创建节点时候,会生成范围为[0-1]的一个随机数,如果这个随机数小于 0.25(相当于概率25%),那么层数就增加 1 层,然后继续生成下一个随机数,直到随机数的结果大于 0.25 结束,最终确定该节点的层数。
这样的做法,相当于每增加一层的概率不超过 25%,层数越高,概率越低,层高最大限制是 64。