还不知道光场相机吗？

1.什么是光场？

光场（light field）：就是指光在每一个方向通过每一个点的光量。

从概念里，你至少可以得到两点信息：

• 光场包含光的方向
• 光场包含一个点的光量

2.什么是光场相机

我们知道普通的相机拍照成像，得到的离散的像素点，每一个像素都会有其像素值，那么这个像素值反应的就是光场中某一点的光量，仅此而已，我们不能够从图像中得到打到这个像素点位置的光线是从哪个方向来的，所以，普通的相机只能够得到光场中的光量信息，丢失了方向信息。

光场相机则不同，不仅能够记录光场的光量信息，也能记录光场中光的方向信息，也就是说它能够记录摄像机内部的整个光场！

光场相机长什么模样，以著名的Lytro公司的光场相机为例， 它们就是下面的模样，左图为第一代产品，名为 Lytro F01，(丑爆了)。右图为第二代产品,名为Lytro Illum (还将就)。

Lytro公司是斯坦福大学的吴义仁（Ren Ng）博士毕业后创办的公司，是世界上首款消费级别的光场相机，还是挺厉害的。他的博士毕业论文名为《Digital Light Field Photography》获得了2006年美国计算机协会(ACM)博士论文大奖。

据说现在已经从公司辞职回到学校教学去了

那光场相机能够记录整个光场又能怎么样呢？

该相机能够实现先拍照后对焦。你没看错，就是这样，在拍完照了，你想重新对焦到图像中哪一个位置，就能通过点击图像得到该位置清晰的图片，放两张Ren Ng论文里《Light field photography with a hand-held plenoptic camera》的图片，对焦平面由近及远，是不是蛮神奇的，消费者不用担心拍到的图片没有聚焦到理想的位置，可以通过后期相机内部对光场的处理实现重聚焦作用(refocus)。

3.工作原理

3.1光场的定义

光场概念最早由A.Gershun在1936年提出，用于描述光在三维空间中的辐射传输特性。1991年，E.Adelson和J.Bergen根据人眼对外部光线的视觉感知，提出用7维函数来表征空间分布的几何光线，称为全光函数(Plenoptic Function)。

$$P(x,y,z,\theta ,\varphi ,\lambda ,t)$$

如果只考虑光线在自由空间的传输，其波长一般不会发生变化，则任一时刻的光线可由5维坐标表示。

$$(x,y,z,\theta ,\varphi )$$

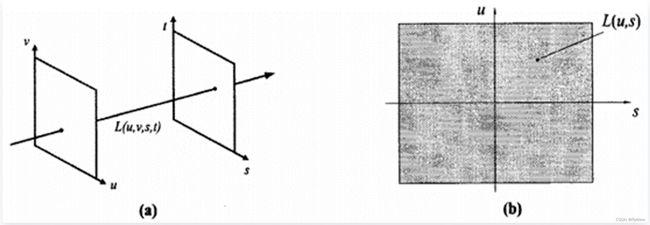
更进一步，忽略光线在传输过程中的衰减，M.levory和P.Hanraham将5维的全光函数降至4维，提出用两个相互平行的平面对四维光场进行参数化表示。

$$L(u,v,s,t)$$

表示光场的一个采样，L表示光线的强度，(u, v) 和 (s, t)分别为光线与两个平面的交点坐标。在四维坐标空间中，一条光线对应光场的一个采样点。现实中大部分成像系统中都可以简化为相互平行的两个平面，比如传统成像系统中的镜头光瞳面和探测器像面，如果用传感器像面中的坐标 (x,y) 表示光线的分布位置，那么镜头光瞳面坐标 (u,v) 就反应了光线的传输方向。

3.2用数码相机采集光场

知道了光场的定义，那么是不是有什么专门的神奇设备能够在空间中采集这样的4维信息呢？没有的，光场虽然听上去比较高大上，可通常采集的办法还是传统的成像系统：相机。最经典的光场采集办法就是相机阵列，比如下图是Stanford Multi-Camera Array：

所以就是把相机排列在了一个平面上而已。为什么这样的相机阵列就采集了光场呢？我们先从最原始的针孔(Pinhole)相机模型谈起：

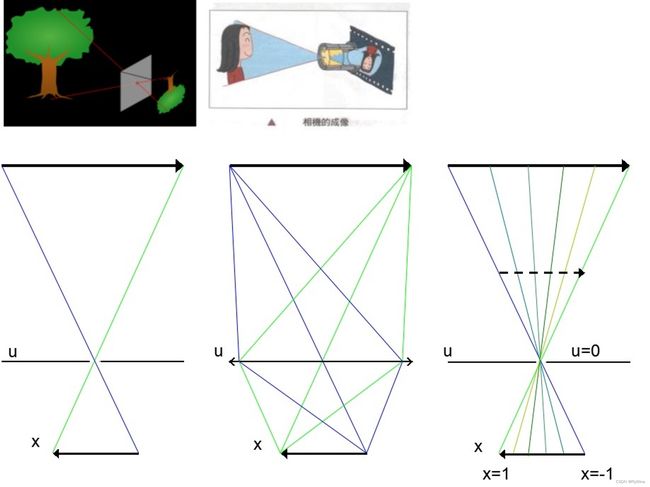
小孔成像模型 是最直观也是最古老的成像模型，小孔相当于把光束的宽度限制得很小，所以如左图光束通过小孔之后再像面上成了一个倒像。这种成像虽然简单，然而一个重大不足是成像的分辨率被小孔大小限制着，小孔越小，则成像越清晰，然而光量也越小，像会很黯淡。

为了成明亮的像我们希望光束的量大，也就是小孔大，但也不希望光束的不集中导致成像模糊，所以很自然的，凸透镜成像解决了这个问题。在凸透镜成像系统中，不过镜头怎么复杂，模式都是和中间的示意图一样，一个空间中的点发出的光束，打在透镜的一块面积上后，折射，然后汇聚到一点。所以单从光线采集的角度而言，和小孔成像系统的没有差别。

那么这和光场的联系在哪呢，回顾前面说的用两个平面上的两点坐标表示广场的办法，如果我们这里把镜头中心所在平面看成uv平面，定义镜头中心为(0,0)，而成像平面，也就是传感器所在平面看成xy平面，则在普通的成像系统中捕捉到的一幅图像可以看成是u=0, v=0出发的光线在传感器平面上的采样，也就是说我们采集了：

$${L(0,0,x,y)|}_{x,y\in \text{ senser plane }}$$

其中每个 L(0,0,x,y) 的值就是传感器上的像素值。一个直观的例子是上图的第三个光路图，简化到二维情况的话，只看 L(u,x)，假设在传感器平面上有6个像素，那么采集到的6条光线就分别是 L(0,-1), L(0,-0.6), L(0,-0.2), L(0,0.2), L(0,0.6), L(0,1)。那么很自然地，如果改变uv的位置，也就是镜头中心的位置，不仅能采集xy平面的光线，uv平面的也可以采集了，所以就能采集整个uv和xy间的光场了，所以相机阵列就相当于在uv平面上布满了很多采样点。

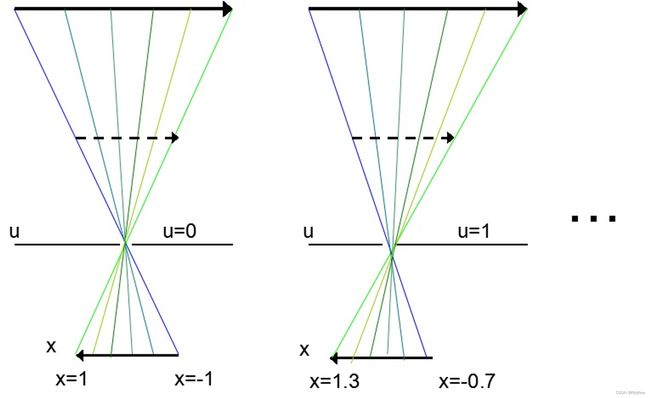
当然，上面说的是最直观最理想的情况，把相机近似成针孔模型还有个前提是景深足够，另外我的例子里xy平面是用传感器所在平面定义，另一种流行的定义方法是用相机的焦平面，也就是在镜头前方，也就是上图中的虚线箭头，这种方法相对来说就更为直观了，尤其是在假设焦距很小的情况下，虚线所在的平面就是相机平面距离为焦距的地方。事实上，在几何光学里，因为光线是严格直线传播，所以沿着光轴中心的不同位置上，如果都能采样的话，那么采到的像都是相似的，所以理论上讲uv和xy平面是可以沿着光路的中心轴任意位置定义的。另外，除了用x和y，也有很多学者喜欢用s和t描述像平面，不过这仅仅是字母使用习惯上的不同。

相机阵列只是采集光场的最基本模型，实际实现的系统都是基于相机阵列的原理，但是具体结构非常不一样。

3.3微镜头阵列采集光场

目前主流还是在使用 微镜头阵列 的方式进行采集光场信息。

基于微透镜阵列的光场采集最早可以追溯到1908年Lippmann提出的集成成像（Integral photography）[5]，集成成像为基于微透镜阵列的光场采集奠定了重要的理论基础。关于集成成像的发展历史，可以参考Roberts在2003年的详细梳理[6]。基于集成成像理论，MIT的Adelson在1992年尝试采用微透镜阵列来制造光场相机[7]，斯坦福Levoy将集成成像应用于显微镜，实现了光场显微镜[8]。

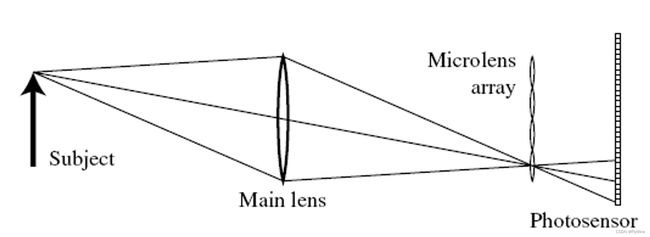
基于透镜阵列的光场采集主要依靠在成像传感器与主镜头之间加入一片微透镜阵列，物体表面光线首先经过主镜头，然后经过微透镜，最后到达成像传感器（e.g. CCD/CMOS）。如图1所示，物体表面A点在FOP角度范围内发出的光线进入相机主镜头并聚焦于微透镜，微透镜将光线分成4x4束，并被成像传感器上对应的16个像素记录。类似的，空间中其它发光点，例如B点和C点，在其FOP角度范围内的光线都被分成4x4束并被分别记录。

3.3.1Lytro

Lytro是由吴义仁（是Levoy的学生）于2006年创立的美国公司，主要开发光场相机。

• Lytro从2012年2月29日开始以8 GB和16 GB版本发售其第一代袖珍相机，能够在拍摄后重新对焦图像。
• 在2014年4月，公司发布了Lytro Illum，这是面向商业和实验摄影师的第二代相机。Lytro Illum发行价格为1600美元。
• 在2015年秋天，Lytro改变了方向，宣布推出Immerge，这是一款带有配套的自定义计算服务器的超高端VR视频捕获相机。Immerge有望在2016年上市，并且对于试图将基于CGI的VR与视频VR相结合的工作室非常有用。
• Lytro于2018年3月下旬停止运营。最初有报道称Lytro被Google收购，但后来又有报道称Lytro的大多数前雇员已转为在Google工作。

这样的技术颇具创新性，甚至乔布斯在去世前也会见了Lytro的创始人。乔布斯曾希望在iPhone中引入这种技术。

Lytro采用的是在传感器表面覆盖一层微镜头阵列，原理图：


微镜头阵列就是类似如下，近距离覆盖在传感器表面：

这个图是Lytro创始人博士论文里的原型机的阵列，(A)是阵列宏观的可视效果，(B)和©是微观结构，后来在Lytro中已经改进成了六边形的镜头阵列。一个Lytro在传感器成像的原始图片如下：

可以看到和相机阵列不同，Lytro采集到的图像是虚脱6边型构成的，不过其实背后的原理都是一样的，这一大幅看着像昆虫眼睛采到的图像是能够通过算法转化成前面提到的相机阵列等效图像的，而每一幅等效的图像又叫Sub-Aperture图像。

3.3.2 Raytrix

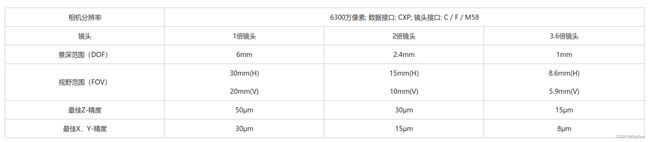
和Lytro类似的还有Raytrix的光场相机，不过Raytrix的采样精度和采样数都大幅高于玩具般的Lytro，属于工业级光场相机。

官网：https://raytrix.de

光场相机是一种新型的3D相机，它可以捕捉标准图像和场景的深度信息。光场相机可以通过单镜头在单次拍摄中只使用可用的光线来捕捉公制的3D信息。Raytrix一直专注于开发工业应用的光场相机。获得专利的微型镜头阵列设计使高有效分辨率和大景深之间达到了最佳折衷。Raytrix相机已经应用于体积测速、植物表型、自动光学检测和显微镜等领域。

Raytrix是一家德国公司，成立于2008年，自2010年开始销售3D光场相机，用于专业应用和研究。我们最初的目标是探索光场技术的潜力，并使其在个人应用中可行。到现在，我们已经是一个高度积极的团队，不断提高光场相机的质量，探索新的应用领域。

Raytrix 光场相机视频

下面罗列一些型号和参数：

国内代理：

• 北京凌云
• 大恒图像

3.3.3Adobe Plenoptic Lenses

和Lytro还有Raytrix不同，Adobe的光场相机把光场采样镜头置于主镜头组前：

3.3.4PiCam

这是个微缩版的相机阵列，用的就是手机上的那种镜头，4x4阵列，特点是用提出的算法优化了分辨率和深度图估计：

微缩相机阵列里还有一个例子发布的华为荣耀6 Plus。

3.3.5奕目科技（VOMMA）

奕目（上海）科技有限公司，于2017年推出了具有国际领先水平的自主知识产权工业光场相机系统，通过仿生昆虫复眼成像，将几十万至几百万个微小复眼传感器精密封装成一台被誉为“工业复眼”的全新一代三维光场相机，实现了“单相机、单次拍摄，三维成像”，解决了“透（玻璃）、薄（薄膜）、微（微精密金属）”三维缺陷、三维尺寸快速精密检测的难题。

奕目科技已成为全球极少数全面掌握光场相机光学设计、封装制造、三维精密快速检测、光场图像三维渲染全部核心技术的光场三维成像科技公司，光场三维测量精度和效率处于国际领先水平，申请及授权国内20余项核心光场技术专利。

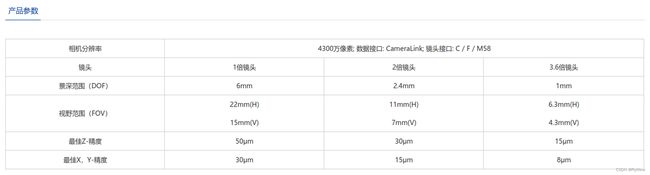
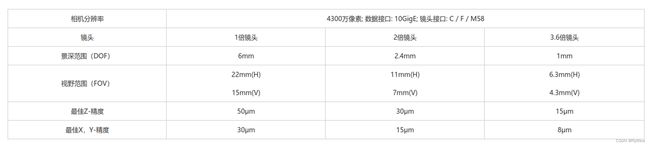
目前主要产品：

• VA4300-M-CL
  
  
  适用场景：

  • 手机OLED屏幕及CPI薄膜缺陷精准三维分层
  • BGA / Wire Bonding三维检测
  • 细微隐藏划痕快速检测
    

• VA4300-M-TGE
  和VA4300-M-CL主要区别为采用10GigE通讯协议，主要参数无变化。
  

• VA6500-M-CXP
  
  
  

3.4基于编码掩膜的光场采集

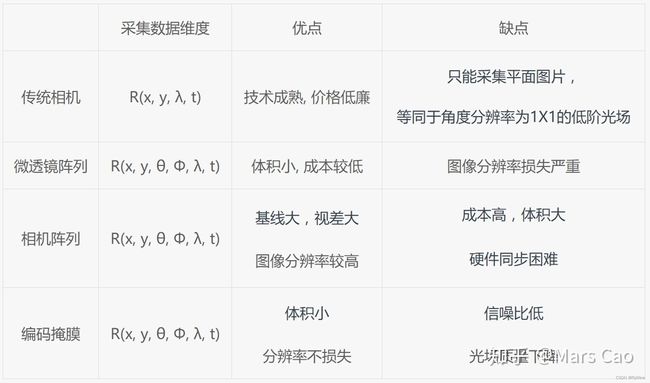
基于微透镜阵列和基于相机阵列的光场采集都有一个共同点——“阵列”。前者通过多个微透镜构成阵列，牺牲图像分辨率换取角度分辨率。后者通过多个相机构成阵列，在不牺牲图像分辨率的情况下增加了角度分辨率，但是需要增加大量的图像传感器。总体而言，视点分辨率与角度分辨率是一对矛盾因素，总是此消彼长。通过增加成像传感器数量来抵消这一矛盾会造成硬件成本的急剧增加。

上述两种光场采集方案必须在图像分辨率和角度分辨率之间进行折中。学术界最新出现的基于编码掩膜的光场采集打破了这一局限。该方案通过对光场的学习去掉光场的冗余性，从而实现了采集更少的数据量而重建出完整的光场。

在传统相机的成像光路中加入一片半透明的编码掩膜，掩膜上每个像素点的光线透过率都不一样（也称为编码模式），进入光圈的光线在到达成像传感器之前会被掩膜调制，经过掩膜调制后的光线到达成像传感器。利用提前学习好的光场字典，从单幅采集的调制图像就可以重建出完整的光场。掩膜的编码模式理论上可以采用随机值，Kshitij Marwah证明了通过约束变换矩阵的转置与变换矩阵的乘积为单位矩阵可以得到优化的编码掩膜，采用优化后的编码掩膜可以重建出更高质量的光场。

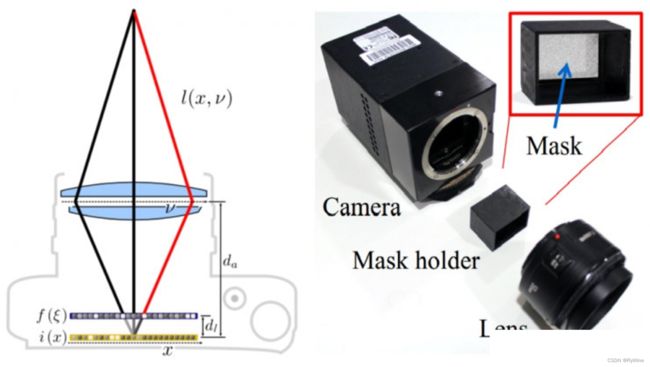
基于编码掩膜的光场采集方案最大的优势在于不需要牺牲图像分辨率就能提高角度分辨率。但该方案存在光场图像信噪比低的缺点，这主要是由于两方面的原因造成：

• 掩膜的透光率不能达到100%，因此会损失光线信号强度，导致成像信噪比低；
• 所重建的最终光场图像并不是成像传感器直接采集得到，而是通过从被调制的图像中进行解调制得到；本质上是基于已经学习的光场字典去“猜”出待重建的光场。

3.6光场采集方案对比

1. 基于微透镜阵列
   • 具有体积小巧
   • 硬件成本低
   • 光场视点图像分辨率损失严重，随着视点数量的增加，单个视点分辨率急剧降低。
   • 受到相机光圈的限制，光场中可观察的视差范围较小。
2. 相机阵列
   • 视点分辨率不损失，由单个相机成像传感器决定。
   • 光场的视差范围更大
   • 需要的相机数量较多，硬件成本高昂，例如采集7x7视点的光场需要49个相机
   • 相机同步控制复杂，数据量大，存储和传输成本高。
3. 编码掩膜
   • 信噪比降低
   • 分辨率不损失

3.5光场和3D

知道了光场的直观意义，那么很自然地就会想到和普通的照片比起来，获取的信息不再是一幅简单的2D像素阵列，而是三维空间中的光线，也就是说光场中是包含三维信息的。一个简单的例子来说明：

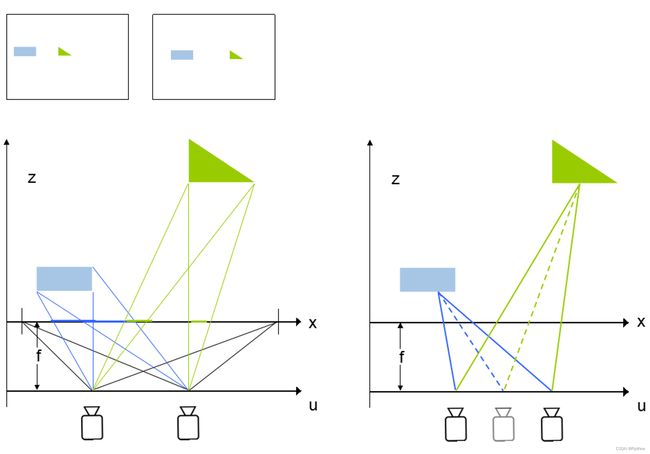
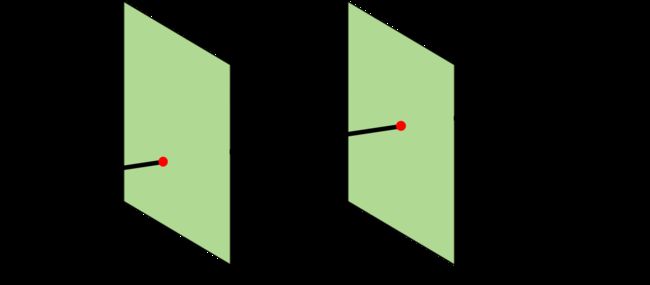
左边的例子是不同uv平面上的相机成像的差别，假设成像后焦平面都取相同的区域的话，可以看到因为uv的不同，所以不同距离上的物体在最终的图像上的位置也不一样，其实这个就是典型的视觉中的Stereo问题。

左边的例子是不同uv平面上的相机成像的差别，假设成像后焦平面都取相同的区域的话，可以看到因为uv的不同，所以不同距离上的物体在最终的图像上的位置也不一样，其实这个就是典型的视觉中的Stereo问题。另外既然提到了Stereo，也需要特别提到的是，在相机阵列采集到不同拍照位置的图像之后，有个非常重要的步骤叫做Calibration，也就是在选定的x平面上，要保证两个相机视野是重合的，如左图所示。那么深度的信息是如何获得的呢，来看下图：

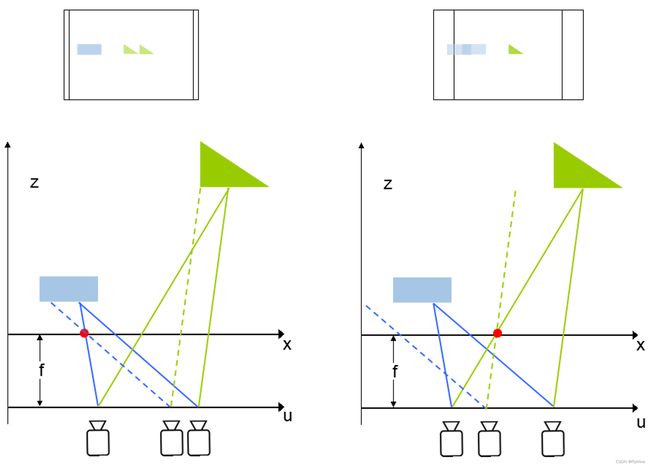
假象我们可以保持右边的相机的光场不变，然后向左平移，使得蓝色的光线在成像面上重合，那么最终蓝色方块在两个相机成像的照片里位置就会完全相同，这其实就等效于把原始位置成的像向左移动了一段距离，然后和左边相机成的图像叠加，那么就会发现蓝色方块重合了。类似的，如右图所示，如果把右边相机成的图像向左移动一大段距离，那么更远的绿色三角图像就重合了，要想是不同位置的物体重合就要对应不同的移动距离，而这个距离实际上是和物体到镜头的距离相关的，通过移动距离和相机采样点之间距离的比值就可以轻易求出，进而就相当于我们得出了蓝色方块和绿色三角的深度信息。

4.光场深度估计算法分类

由上可知，光场图像中包含来自场景的多视角信息，这使得深度估计成为可能。相较于传统的多视角深度估计算法而言，基于光场的深度估计算法无需进行相机标定，这大大简化的深度估计的流程。但是由于光场图像巨大导致了深度估计过程占用大量的计算资源。同时这些所谓的多个视角之间虚拟相机的基线过短，从而可能导致误匹配的问题。以下将对多种深度估计算法进行分类并挑选具有代表性的算法进行介绍。

4.1多视角立体匹配

根据光场相机的成像原理，我们可以将光场图像想像成为多个虚拟相机在多个不同视角拍摄同一场景得到图像的集合，那么此时的深度估计问题就转换成为多视角立体匹配问题。以下列举几种基于多视角立体匹配算法的深度估计算法。

• Jeon, Hae Gon, et al. Accurate depth map estimation from a lenslet light field camera. Computer Vision and Pattern Recognition IEEE, 2015:1547-1555.
• Yu, Zhan, et al. Line Assisted Light Field Triangulation and Stereo Matching. IEEE International Conference on Computer Vision IEEE, 2014:2792-2799
• Heber, Stefan, and T. Pock. Shape from Light Field Meets Robust PCA. Computer Vision – ECCV 2014. 2014:751-767
• Heber, Stefan, R. Ranftl, and T. Pock. Variational Shape from Light Field. Energy Minimization Methods in Computer Vision and Pattern Recognition. Springer Berlin Heidelberg, 2013:66-79
• Chen, Can, et al. Light Field Stereo Matching Using Bilateral Statistics of Surface Cameras. IEEE Conference on Computer Vision and Pattern Recognition IEEE Computer Society, 2014:1518-1525

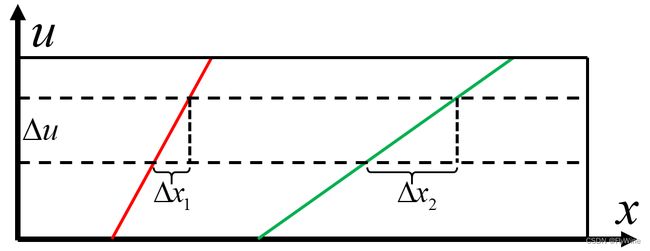
4.2基于EPI的方法

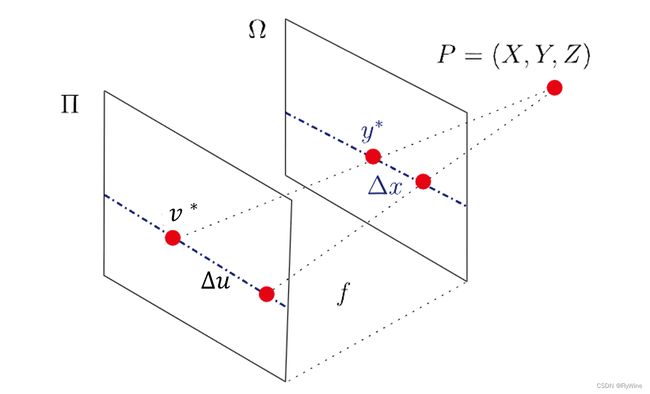
不同于多视角立体匹配的方式，EPI的方式是通过分析光场数据结构的从而进行深度估计的方式。EPI图像中斜线的斜率就能够反映出场景的深度。上图中点P为空间点，平面II为相机平面，平面$\Omega$为像平面。图中$\Delta u$与$\Delta x$的关系可以表示为如下公式：

$$\Delta x=-\frac{f}{Z}\Delta u,$$

假如固定相同的$\Delta u$，水平方向位移较大的EPI图中斜线所对应的视差就越大，即深度就越小。如下图所示，$\Delta x_2>\Delta x_1$，那么绿色线所对应的空间点要比红色线所对应的空间点深度小。

以下列举几种基于EPI的深度估计算法:

• Kim, Changil, et al. Scene reconstruction from high spatio-angular resolution light fields. Acm Transactions on Graphics 32.4(2017):1-12.
• Li, J., M. Lu, and Z. N. Li. Continuous Depth Map Reconstruction From Light Fields. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society 24.11(2015):3257
• Krolla, Bernd, et al. Spherical Light Fields. British Machine Vision Conference 2014.
• Wanner, Sven, C. Straehle, and B. Goldluecke. Globally Consistent Multi-label Assignment on the Ray Space of 4D Light Fields. IEEE Conference on Computer Vision and Pattern Recognition IEEE Computer Society, 2013:1011-1018
• Diebold, Maximilian, B. Jahne, and A. Gatto. Heterogeneous Light Fields. Computer Vision and Pattern Recognition IEEE, 2016:1745-1753.
• Zhang S, Sheng H, Li C, et al. Robust depth estimation for light field via spinning parallelogram operator. Computer Vision and Image Understanding, 2016, 145:148-159
• Wanner S, Goldluecke B. Reconstructing reflective and transparent surfaces from epipolar plane images. In German Conference on Pattern Recognition (Proc. GCPR), 2013:1-10.
• S. Wanner and B. Goldluecke. Globally Consistent Depth Labeling of 4D Light Fields. 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 2012, pp. 41-48, doi: 10.1109/CVPR.2012.6247656.

4.3 散焦及融合的方法

光场相机一个很重要的卖点是先拍照后对焦，这其实是根据光场剪切原理得到的。通过衡量像素在不同焦栈处的“模糊度”可以得到其对应的深度。以下列举几种基于散焦的深度估计算法:

• Wang, Ting Chun, A. A. Efros, and R. Ramamoorthi. Occlusion-Aware Depth Estimation Using Light-Field Cameras. IEEE International Conference on Computer Vision IEEE, 2016:3487-3495.
• Tao, M. W, et al. Depth from Combining Defocus and Correspondence Using Light-Field Cameras. IEEE International Conference on Computer Vision IEEE Computer Society, 2013:673-680.
• Tao, Michael W., et al. Depth from shading, defocus, and correspondence using light-field angular coherence. Computer Vision and Pattern Recognition IEEE, 2015:1940-1948.
• Williem W, Kyu P I. Robust light field depth estimation for noisy scene with occlusion. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016:4396-4404.
• Williem W, Park I K, Lee K M. Robust light field depth estimation using occlusion-noise aware data costs. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 2017(99):1-1.

4.4 深度学习

目前而言，将深度学习应用于从双目或者单目中恢复深度已经不再新鲜，但是将其应用于光场领域进行深度估计的算法还真是寥寥无几。不过总有一些勇敢的践行者去探索如何将二者结合，以下列举几种基于学习的深度估计算法：

• Johannsen, Ole, A. Sulc, and B. Goldluecke. Variational Separation of Light Field Layers. (2015)
• Heber, Stefan, and T. Pock. Convolutional Networks for Shape from Light Field. Computer Vision and Pattern Recognition IEEE, 2016:3746-3754.
• Johannsen O, Sulc A, Goldluecke B. What sparse light field coding reveals about scene structure. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016(1/3/4):3262-3270.
• Heber S, Yu W, Pock T. U-shaped networks for shape from light field. British Machine Vision Conference, 2016, 37:1-12.
• Heber S, Yu W, Pock T. Neural EPI-Volume networks for shape from light field. IEEE International Conference on Computer Vision (ICCV), IEEE Computer Society, 2017:2271-2279.
• Jeon H G, Park J, Choe G, et.al. Depth from a Light Field Image with Learning-based Matching Costs. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 2018.
• Shin C, Jeon H G, Yoon Y. EPINET: A Fully-Convolutional Neural Network for Light Field Depth Estimation Using Epipolar Geometry. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018.

5.参考相关文献

• 光场相机是如何实现的？
• 漫谈计算摄影学 (一)：直观理解光场(Light Field)
• Mars说光场（3）— 光场采集
• Light Field Depth Estimation