数据结构之栈的应用--中缀表达式转后缀表达式与（简单）表达式的计算

转载大佬的博客，不过代码加了注释可能对学习更友好

作者：凛冬烈焰
来源：CSDN
原文：https://blog.csdn.net/qq_26286193/article/details/80214805

“计算中缀表达式”可以称得上是一个特别经典的关于栈的算法题，几乎在所有数据结构教材中都会涉及，而且很多公司面试或者笔试的时候都会把这道题作为一个考察点。可以说，这是一道必须要掌握的算法题。中缀表达式、后缀表达式等概念在这里就不赘述了，让我们直奔主题。

题目：输入一个中缀表达式，计算其结果。

输入的前提假设：

（1）只考虑+、-、*、/这四种运算符，中缀表达式中只有一种括号：（）；

（2）输入的中缀表达式中只有整数，没有小数；

（3）假定输入是合法的。

很多文章或课本喜欢一步到位，直接讨论如何从中缀表达式计算结果。但对于初学者来说，跨度未免大了点。这里循序渐进，从易到难，先讨论如何将中缀表达式转化为后缀表达式，再讨论如何计算后缀表达式。最后在前面两步的基础上，讨论如何一步到位，直接计算中缀表达式的结果：

一、如何将中缀表达式转化为后缀表达式

在日常应用中，算术表达式中运算符总是出现在两个操作数之间，例如5*（7-2*3）+8/2，这种形式称为中缀表达式。计算一个中缀表达式需要知道运算符的优先级和结合性。乘除是高优先级，加减是低优先级，优先级相同时他们都是左结合的，也就是从左计算到右。有括号就要计算括号内的表达式。

中缀表达式利于人的理解，但不便于计算机的处理。因此需要将中缀表达式转换成后缀表达式，以方便计算机处理。所谓后缀表达式就是将运算符放在运算数之后。后缀表达式也称为逆波兰表达式。

比如：

中缀表达式为：1+(2-3)*4+4/2

对应后缀表达式为：1 2 3 - 4* + 4 2 / +

如何将一个中缀表达式转化为后缀表达式？我们需要借助栈的力量，用它来存放运算符。算法流程如下：

首先将各种运算符（包括括号）的优先级排列如下（数字越大，优先级越高）：

1：（

2：+ -

3：* /

4：）

对输入的中缀表达式从左到右遍历：

1）如果遇到数字，直接添加到后缀表达式末尾；

2）如果遇到运算符+、-、*、/：

先判断栈是否为空。若是，则直接将此运算符压入栈。若不是，则查看当前栈顶元素。若栈顶元素优先级大于或等于此操作符级别，则弹出栈顶元素，将栈顶元素添加到后缀表达式中，并继续进行上述判断。如果不满足上述判断或者栈为空，将这个运算符入栈。要注意的是，经过上述步骤，这个运算符最终一定会入栈。

3）如果遇到括号：

如果是左括号，直接入栈。如果是右括号，弹出栈中第一个左括号前所有的操作符，并将左括号弹出。（右括号别入栈）。

4）字符串遍历结束后，如果栈不为空，则弹出栈中所有元素，将它们添加到后缀表达式的末尾，直到栈为空。

二、计算后缀表达式

后缀表达式的计算就相当简单了。准备一个数字栈。从左到右扫描后缀表达式，如果是数字，放入数字栈。如果是符号，从数字栈中弹出两个数字，第一个取出的数字为右运算数，第二个为左运算数，进行运算。然后将结果放进数字栈中。如此反复，直到读完整个表达式后，留在数字栈中的那个数字就是最终结果。

C++代码如下，要注意，下面的代码默认中缀表达式中所有数字都是整数，并且都在0到9之间。而且计算结果都是整数（比如5/2=2）。

#include <iostream> 
#include <cstring>
#include <stack>
using namespace std;

int getPriority(char ch)
{//获取优先级
	if(ch == '(') return 1;
	else if(ch == '+' || ch == '-') return 2;
	else if(ch == '*' || ch == '/')	return 3;
	else return 4; 
}

string getPostfixExpression(string str)
{   //将中缀表达式转化为后缀表达式
	//默认输入合法
	stack<char> mystack;
	int size = str.size();
	int i= 0 ;
	char tmp;
	string res = "";
	while(i < size)
	{
		if(str[i] >= '0' && str[i]<='9')
		{//数字直接进字符串 
			res.push_back(str[i]);
		}
		else if(str[i] == '+' || str[i] == '-' || str[i] == '*' || str[i] == '/')
		{//如果是操作符 
			if(mystack.empty())
			{//栈中是空的直接进栈 
				mystack.push(str[i]);	
			}	
			else
			{
				while(!mystack.empty())
				{
					tmp = mystack.top();
					//弹出栈顶元素与当前操作符对比
					if(getPriority(tmp) >= getPriority(str[i]))
					{//若栈顶元素比当前操作符优先级高 
						res.push_back(tmp);//弹出栈顶操作符加入后缀表达式 
						mystack.pop();
					}
					else break;//若栈顶元素比当前操作符优先级低，跳过 
				}
				mystack.push(str[i]);//最终一定会将该运算符入栈
			}
		}
		else//处理括号 
		{
			if(str[i] == '(') mystack.push(str[i]);	//左括号进符号栈 
			else
			{//如果是右括号，弹出符号栈中第一个左括号前所有的操作符，并将左括号弹出 
				while(mystack.top() != '(')	
				{//弹出符号栈中第一个左括号前所有的操作符加入后缀表达式字符串里 
					tmp = mystack.top();
					res.push_back(tmp);
					mystack.pop(); 
				}
				mystack.pop(); //将左括号弹出 
			} 
		}	
		i++;//while(i
	} 
	//遍历完后
	while(!mystack.empty())
	{//若符号栈不为空 
		tmp = mystack.top();
		res.push_back(tmp);//依次加入后缀表达式 
		mystack.pop();	
	} 
	return res;//返回后缀表达式 
}

int calculator(string str)
{//计算后缀表达式的值，默认中缀表达式所有数字都是一位的，在0~9之间
	stack<int> mystack;
	int size = str.size();
	int num1,num2,result;
	for(int i=0;i<size;i++)
	{
		if(str[i] >= '0' && str[i] <= '9')
		{
			mystack.push(str[i] - '0');	
		}
		else
		{//取数字栈顶两个数字元素与操作符栈顶的操作符进行运算 
			num2 = mystack.top();
			mystack.pop();
			num1 = mystack.top();
			mystack.pop();
			if(str[i] == '+')	result = num1 + num2;
			else if(str[i] == '-') result = num1 - num2;
			else if(str[i] == '*') result = num1 * num2;
			else if(str[i] == '/') result = num1 / num2;
			mystack.push(result);//将本次运算结果压入数字栈作为下一次运算的右操作数 
		}
	}  
	return mystack.top();//返回运算结果 
} 

int main()
{
	string str="1+(2-3)*4+4/2";
    cout <<"中缀表达式为:"<< endl << str << endl;
    string res = getPostfixExpression(str);
    cout <<"后缀表达式为:"<< endl << res << endl;
    int num_res = calculator(res);
    cout <<"计算结果:"<< endl << num_res << endl;
    system("pause");
    return 0;
}

三、直接计算中缀表达式

其实将前面的两步结合起来，就可以得到直接计算的方法。准备一个数字栈和一个符号栈。

从左到右遍历中缀表达式。如果遇到数字，入数字栈。

如果遇到符号（四个运算符以及括号），跟前面的“中缀表达式转后缀表达式”过程一样，对符号栈进行处理。处理过程中，对每一个出栈的运算符：+ - * /，根据“计算后缀表达式”的方法，计算结果（跟数字栈配合）。

如果遍历完中缀表达式后符号栈还非空，就继续出符号栈的运算符，计算，直到符号栈为空。最后数字栈剩下的数字就是结果。

下面给出用C++实现“计算中缀表达式”的代码，里面考虑了“数字不止1位”，并且用浮点型来表示最终运算结果。要求中缀表达式中只能包含整数和运算符（不能包含小数），并且是合法的。

#include <iostream> 
#include <cstring>
#include <stack>
#include <cstdlib>
using namespace std;

int getPriority(char ch)
{//获取优先级
	if(ch == '(') return 1;
	else if(ch == '+' || ch == '-') return 2;
	else if(ch == '*' || ch == '/')	return 3;
	else return 4; 
}

void calculate(stack<double> &mystack, char operation)
{
	double num1,num2,result;
	num2 = mystack.top();//右运算数 
	mystack.pop();
	num1 = mystack.top();//左运算数
	mystack.pop(); 
	if(operation == '+')	result = num1 + num2;		
	else if(operation == '-') result = num1 - num2;
	else if(operation == '*') result = num1 * num2;
	else if(operation == '/') result = num1 / num2;
	
	mystack.push(result);//将本次运算结果压入数字栈作为下一次运算的右操作数	
} 

double calculator(string str)
{
	//计算中缀表达式，默认输入是合法的
	stack<double> mystack_number;//运算数栈 
	stack<char> mystack_operation;//运算符栈
	int i=0,j;
	int size = str.size();//前缀表达式字符串 
	char tmp_operation;
	string tmp_num;
	
	while(i<size)
	{
		if(str[i] >= '0' && str[i] <= '9')
		{//如果是数字 
			j = i;
			while(j < size && str[j] >= '0' && str[j] <= '9')	j++;
			tmp_num = str.substr(i,j-i);//用子串提取该数 
			mystack_number.push(atoi(tmp_num.c_str()));//将其转化为数字压入数字栈 
//C语言atoi()把字符串转换成整型数
//.c_str()函数返回一个指向正规C字符串的指针常量,内容与本string串相同
			i = j;//更新后缀表达式遍历指针 
		}
		else if(str[i] == '+' || str[i] == '-' || str[i] =='*' || str[i] == '/')
		{//如果是运算符 
			if(mystack_operation.empty())
			{//操作符栈为空，操作符直接入栈 
				mystack_operation.push(str[i]);
			}
			else
			{//否则需要和栈顶操作符比较 
				while(!mystack_operation.empty())
				{
					tmp_operation = mystack_operation.top();//操作符栈栈顶 
					if(getPriority(tmp_operation) >= getPriority(str[i]))
					{//如果操作符栈栈顶符号优先级高于当前后缀表达式符号优先级 
						calculate(mystack_number,tmp_operation);//计算 
						mystack_operation.pop();//弹出操作符栈栈顶 
					}
					else break;//操作符栈栈顶符号 > 当前后缀表达式符号优先级 
				}
				mystack_operation.push(str[i]);//不管进不进行运算，都需要将表达式中的运算符压入运算符栈 
			}
			i++;//while(i
		}
		else
		{//如果是括号 
			if(str[i] == '(') mystack_operation.push(str[i]);//左括号直接入符号栈
			else
			{
				while(mystack_operation.top() != '(')	//这里有限定，不是左括号就是右括号
				{//右括号则符号栈出栈运算直到左括号 
					tmp_operation = mystack_operation.top();
					calculate(mystack_number,tmp_operation);
					mystack_operation.pop();	
				} 
				mystack_operation.pop();//弹出左括号 
			} 
			i++;//while(i
		}
	}
	//遍历完后，若栈非空，弹出所有元素
	while(!mystack_operation.empty())
	{
		tmp_operation = mystack_operation.top();
		//计算
		calculate(mystack_number,tmp_operation);
		mystack_operation.pop();	
	} 
	return mystack_number.top();//返回数字栈的栈顶，即计算结果 
} 

int main()
{
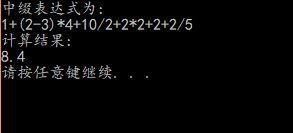
	string str = "1+(2-3)*4+10/2+2*2+2+2/5";
	cout << "中缀表达式为:" << endl << str << endl;
	double num_res = calculator(str);
	cout << "计算结果:" << endl << num_res << endl;
	system("pause");
	return 0;
}

【参考资料】

[1]https://blog.csdn.net/sinat_36118270/article/details/70257547

[2]翁惠玉, 俞勇. 数据结构:思想与实现[M]. 高等教育出版社, 2009.