动态规划-买卖股票的最佳时机 IV

1 题目

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格，和一个整型 k 。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

2 示例

2.1 示例 1：

输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

2.2 示例 2：

输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

2.3 提示：

0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

3 算法题解

3.1 解题思路

1. 如果k > n / 2，这该算法题就演化为买卖股票的最佳时机 II可以买卖任意多次；
2. 其他的就类似于买卖股票的最佳时机 III算法题

3.2 记录阶段的处理方法

我们在处理的时候需要记录阶段，每个阶段的含义如下所示：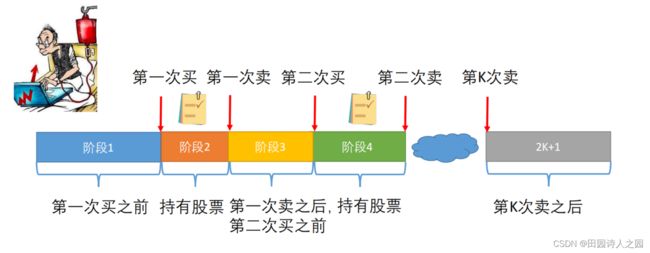
阶段1：没有买卖过
阶段3：买卖过一次，手中无股票
…
阶段2K+1：买卖过K次股票，手中无股票

阶段2：没有买卖过，手中有股票
阶段4：买卖过一次，手中有股票
…
阶段2K:买卖过k - 1次，手中有股票

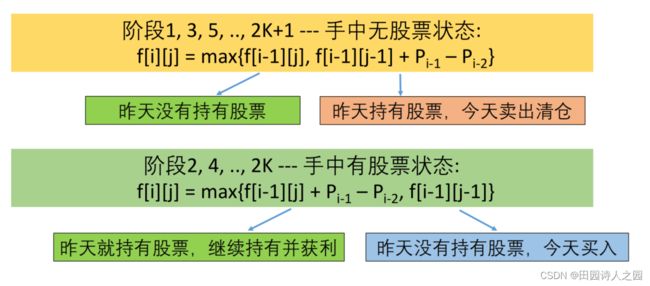
3.3 转移方程

3.4 初始条件和边界条件

前0天处于阶段1：
f[0][0] = f[0][1] = 0;
f[0][2] = f[0][3] = f[0][4] … = f[0][2k+1] = INT_MIN;

阶段1，3, 5，… 2k + 1:
f[i][j] = max{f[i-1][j], f[i-1][j-1] + Pi-1 – Pi-2}
阶段2，4， 6，… 2k:
f[i][j] = max{f[i-1][j] + Pi-1 – Pi-2, f[i-1][j-1]}

如果j - 1 < 1 或i - 2 < 0 对应的项不计算
最大值是max{f[N][1], f[N][3], …, f[N][2K+1]}

3.5 算法代码实现

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        if (n == 0) {
            return 0;
        }

        int i, j;
        int res = 0;
        if (k > n/2) {
            for (i = 0; i < n - 1; i++) {
                if (prices[i] < prices[i + 1]) {
                    res += prices[i + 1] - prices[i];
                }
            }

            return res;
        }

        int m = k;
        vector<vector<int> > dp(n + 1, vector<int>(2 * m + 2));

        dp[0][0] = dp[0][1] = 0;
        for (i = 2; i < 2 * m + 1; i++) {
            dp[0][i] = INT_MIN;
        }

        for (i = 1; i < n + 1; i++) {
            // phase 1, 3, 5 ..., 2k + 1
            for (j = 1; j <= 2 * m + 1; j += 2) {
                dp[i][j] = dp[i - 1][j];
                if (j > 1 && i >= 2 && dp[i - 1][j - 1] != INT_MIN) {
                    dp[i][j] = max(dp[i][j], dp[i -1][j - 1] + prices[i - 1] - prices[ i - 2]);
                }
            }

            //phase 2, 4, 6 ..., 2k
            for (j = 2; j <= 2 * m; j += 2) {
                dp[i][j] = dp[i - 1][j - 1];
                if (i >= 2 && dp[i - 1][j] != INT_MIN) {
                    dp[i][j] = max(dp[i][j], dp[i - 1][j] + prices[i - 1] - prices[i - 2]);
                }
            }
        }

        res = 0;
        for (i = 1; i <= 2 * m + 1; i += 2) {
            res = max(res, dp[n][i]);
        }

        return res;
    }
};