sigmoid和softmax激活函数的区别
一、简单说下sigmoid激活函数
解析:
常用的非线性激活函数有sigmoid、tanh、relu等等,前两者sigmoid/tanh比较常见于全连接层,后者relu常见于卷积层。这里先简要介绍下最基础的sigmoid函数(btw,在本博客中SVM那篇文章开头有提过)。
其中z是一个线性组合,比如z可以等于:b + w1x1 + w2x2。通过代入很大的正数或很小的负数到g(z)函数中可知,其结果趋近于0或1。
(一般用于全连接+激活函数)
总之,sigmod函数,是逻辑斯蒂回归的压缩函数,它的性质是可以把分隔平面压缩到[0,1]区间一个数(向量),在线性分割平面值为0时候正好对应sigmod值为0.5,大于0对应sigmod值大于0.5、小于0对应sigmod值小于0.5;0.5可以作为分类的阀值;
exp的形式最值求解时候比较方便,用相乘形式作为logistic损失函数,使得损失函数是凸函数;不足之处是sigmod函数在y趋于0或1时候有死区,控制不好在bp形式传递loss时候容易造成梯度弥撒。
二、sigmoid 与 softmax 的区别:
激活函数介绍
对于熟悉机器学习或神经网络的读者来说,sigmoid与softmax两个激活函数并不陌生,但这两个激活函数在逻辑回归中应用,也是面试和笔试会问到的一些内容,掌握好这两个激活函数及其衍生的能力是很基础且重要的,下面为大家介绍下这两类激活函数。sigmoid激活函数从函数定义上来看,sigmoid激活函数的定义域能够取任何范围的实数,而返回的输出值在0到1的范围内。sigmoid函数也被称为S型函数,这是由于其函数曲线类似于S型,在下面的内容中可以看到。此外,该函数曲线也可以用于统计中,使用的是累积分布函数。
softmax函数的基本属性,输入值越大,其概率越高。
多类分类及多标签分类
多类分类意味着候选集是一个多分类,而不仅仅是二分类,不是是与否的问题,而是属于多类中哪一类的问题。一个样本属于且只属于多个分类中的一个,一个样本只能属于一个类,不同类之间是互斥的。举例而言,MNIST数据集,常用的数字手写体识别数据集,它的标签是一个多分类的过程
而对于多标签分类而言,一个样本的标签不仅仅局限于一个类别,可以具有多个类别,不同类之间是有关联的。比如一件衣服,其具有的特征类别有长袖、蕾丝等属性等,这两个属性标签不是互斥的,而是有关联的。
使用softmax和sigmoid激活函数来做多类分类和多标签分类
在实际应用中,一般将softmax用于多类分类的使用之中,而将sigmoid用于多标签分类之中,对于图像处理而言,网络模型抽取图像特征的结构基本相同,只是根据不同的任务改变全连接层后的输出层。下面介绍如何使用softmax和sigmoid完成对应的分类任务。
softmax激活函数应用于多类分类
假设神经网络模型的最后一层的全连接层输出的是一维向量logits=[1,2,3,4,5,6,7,8,9,10],这里假设总共类别数量为10,使用softmax分类器完成多类分类问题,并将损失函数设置为categorical_crossentropy损失函数
首先用softmax将logits转换成一个概率分布,然后取概率值最大的作为样本的分类 。softmax的主要作用其实是在计算交叉熵上,将logits转换成一个概率分布后再来计算,然后取概率分布中最大的作为最终的分类结果,这就是将softmax激活函数应用于多分类中。
sigmoid激活函数应用于多标签分类
sigmoid一般不用来做多类分类,而是用来做二分类,它是将一个标量数字转换到[0,1]之间,如果大于一个概率阈值(一般是0.5),则认为属于某个类别,否则不属于某个类别。这一属性使得其适合应用于多标签分类之中,在多标签分类中,大多使用binary_crossentropy损失函数。它是将一个标量数字转换到[0,1]之间,如果大于一个概率阈值(一般是0.5),则认为属于某个类别。本质上其实就是针对logits中每个分类计算的结果分别作用一个sigmoid分类器,分别判定样本是否属于某个类别同样假设,神经网络模型最后的输出是这样一个向量logits=[1,2,3,4,5,6,7,8,9,10], 就是神经网络最终的全连接的输出。这里假设总共有10个分类。
sigmoid应该会将logits中每个数字都变成[0,1]之间的概率值,假设结果为[0.01, 0.05, 0.4, 0.6, 0.3, 0.1, 0.5, 0.4, 0.06, 0.8], 然后设置一个概率阈值,比如0.3,如果概率值大于0.3,则判定类别符合,那么该输入样本则会被判定为类别3、类别4、类别5、类别7及类别8。即一个样本具有多个标签。
在这里强调一点:将sigmoid激活函数应用于多标签分类时,其损失函数应设置为binary_crossentropy。
sigmoid的函数表达式如下:
![]()
softmax函数形式如下:
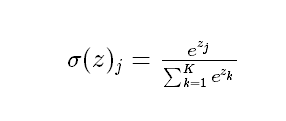
总结:sigmoid将一个real value映射到(0,1)的区间(当然也可以是(-1,1)),这样可以用来做二分类。而softmax把一个k维的real value向量(a1,a2,a3,a4…)映射成一个(b1,b2,b3,b4…)其中bi是一个0-1的常数,然后可以根据bi的大小来进行多分类的任务,如取权重最大的一维。