基础算法 第七课——归并排序

导言

这，是一篇现学现卖的文章。因为，我根本没学过归并排序。所以，这篇文章，绝对能让您学懂归并。如果不懂，那我就再学一遍，再教一遍。

归并排序的概念

从字面上分析，排序就是排序，归并就是归并。它们结合起来，就可以理解为用归并的方法来进行排序。

归并：
还是从字面上分析，归就想成是回归，并就想成是合并。为什么要合并呢？那肯定是已经分散的数据要合起来啊。那么，就很好理解了：归并就是将某些分散的数据合并起来。

知道归并的意思，就能够理解归并排序的意思了：先将一组无序的序列分散至独立的个体，再将已有序的子序列合并，得到完全有序的序列。

步骤说明

1. 将已有数列一分为二，使其分解为左右两组。
2. 重复执行步骤1，直至其分解成单独一个的个体。
3. 定义两个指针，初始分别指向相邻两个子集的左端点。
4. 比较当前两个指针所指数据大小，按照一定规律加入合并数列。
5. 每次比较后，左指针右移一位，若左指针表示的数据大于右指针表示的数据，右指针右移一位。
6. 重复执行步骤3、4、5，直至指针所指位置为空，即超出数据集范围。
7. 重复执行3、4、5、6，直至合并为一组数列。

逐步分析

（图片源于网络）

STEP1

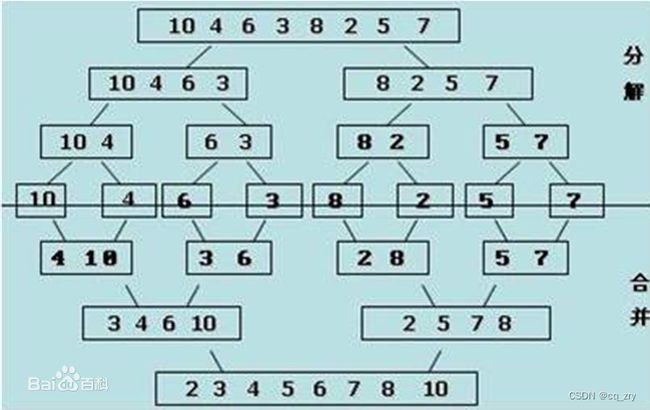
如图，我们先将数列分开来。分开数列很简单吧？我们就定义一个中间值，中间值以前的为左数据集，中间值以后的为右数据集。然后，就可以分别继续拆分，直到该数据集的左端点大于等于右端点。像这样：

void ms(int l,int r)//merge sort，l表示数据集左端点，r表示数据集右端点
{
	//SETP1
	if(l>=r)//不能再分了
	{
		return ;
	}
	
	int mid=(l+r)/2;//中间值
	
	ms(l,mid);//分别继续拆分
	ms(mid+1,r);
}

STEP2

既然已经分解完了，那么就该合并了。如何合并呢？我们可以定义一个数组 $b$ 用来存放合并时的数字。按照步骤说明的方法，我们定义两个指针 $i,j$，一个指向左数据集，一个指向右数据集。但是，我们好像还需要一个指针 $k$，用来指向 $b$ 数组的下标，以便存放数据。定义如下：

void ms(int l,int r)//merge sort，l表示数据集左端点，r表示数据集右端点
{
	//SETP1
	if(l>=r)//不能再分了
	{
		return ;
	}
	
	int mid=(l+r)/2;//中间值
	
	ms(l,mid);//分别继续拆分
	ms(mid+1,r);
	
	//STEP2
	int i=l,j=mid+1;//左右指针
	int k=l;//在l到r的数据中，b数组下标也是l到r
}

STEP3

最关键的一步来了。既然要合并，那么根据步骤说明，我们就需要比较 $a[i],a[j]$ 的大小。如果 $a[i]<a[j]$，$b[k]$ 就存 $a[i]$，并且把 $i,k$ 加一。如果 $a[i]>a[j]$，$b[k]$，就代表当前左指针已经不能再打了，再打的话就不能使最终数列有序。于是我们将 $a[j]$ 存进 $b[k]$，并且把 $j,k$加一。代码如下：

void ms(int l,int r)//merge sort，l表示数据集左端点，r表示数据集右端点
{
	//SETP1
	if(l>=r)//不能再分了
	{
		return ;
	}
	
	int mid=(l+r)/2;//中间值
	
	ms(l,mid);//分别继续拆分
	ms(mid+1,r);
	
	//STEP2
	int i=l,j=mid+1;//左右指针
	int k=l;//在l到r的数据中，b数组下标也是l到r
	
	//STEP3
	while(i<=mid&&j<=r)//只要指针没越界，就循环
	{
		if(a[i]<a[j])//按照分析进行
		{
			b[k]=a[i];
			i++,k++;
		}
		else
		{
			b[k]=a[j];
			j++,k++;
		}
	}
}

STEP4

上面的程序，有一个问题啊，那就是：循环的条件是同时满足指针 $i,j$ 均没有越界。所以在循环结束后，如果指针 $i,j$ 中，有一个还没有指到边界呢？那些剩下的值怎么办呢？很好办啊，我们直接将其接在数组后面就可以啦！为什么可以这样做？因为在循环结束后，剩下的值绝对是大于等于当前 $b$ 数组的最后一位的。所以可以直接接在后面。代码：

void ms(int l,int r)//merge sort，l表示数据集左端点，r表示数据集右端点
{
	//SETP1
	if(l>=r)//不能再分了
	{
		return ;
	}
	
	int mid=(l+r)/2;//中间值
	
	ms(l,mid);//分别继续拆分
	ms(mid+1,r);
	
	//STEP2
	int i=l,j=mid+1;//左右指针
	int k=l;//在l到r的数据中，b数组下标也是l到r
	
	//STEP3
	while(i<=mid&&j<=r)//只要指针没越界，就循环
	{
		if(a[i]<a[j])//按照分析进行
		{
			b[k]=a[i];
			i++,k++;
		}
		else
		{
			b[k]=a[j];
			j++,k++;
		}
	}
	
	//STEP4
	while(i<=mid)//两种情况都有可能
	{
		b[k]=a[i];
		i++,k++;
	}
	while(j<=r)
	{
		b[k]=a[j];
		j++,k++;
	}
}

STEP5

相邻的左右两组数据集已经合并完啦！但是，它是存在 $b$ 数组里的，所以我们还要将其复制给 $a$ 数组：

void ms(int l,int r)//merge sort，l表示数据集左端点，r表示数据集右端点
{
	//SETP1
	if(l>=r)//不能再分了
	{
		return ;
	}
	
	int mid=(l+r)/2;//中间值
	
	ms(l,mid);//分别继续拆分
	ms(mid+1,r);
	
	//STEP2
	int i=l,j=mid+1;//左右指针
	int k=l;//在l到r的数据中，b数组下标也是l到r
	
	//STEP3
	while(i<=mid&&j<=r)//只要指针没越界，就循环
	{
		if(a[i]<a[j])//按照分析进行
		{
			b[k]=a[i];
			i++,k++;
		}
		else
		{
			b[k]=a[j];
			j++,k++;
		}
	}
	
	//STEP4
	while(i<=mid)//两种情况都有可能
	{
		b[k]=a[i];
		i++,k++;
	}
	while(j<=r)
	{
		b[k]=a[j];
		j++,k++;
	}
	
	//STEP5
	for(int I=l;I<=r;I++)
	{
		a[I]=b[I];
	}
}

STEP6

已经完成了，这一步是调用的步骤。如果您学懂了，那么应该知道，调用的步骤就为：ms(数组起始下标,数组终止下标);。

STEP0

以上内容是从小到大排序的方法，如果从大到小，我们只需改一改判断。当然，归并排序还可以将两组数据排列成一组数据，对吧？下面，我将演示如何将两组数据按从小到大的顺序排成一组：

#include

using namespace std;

int x[10000000],y[10000000];

int b[20000000];

void ms(int a[],int l,int r)//merge sort，l表示数据集左端点，r表示数据集右端点
{
	//SETP1
	if(l>=r)//不能再分了
	{
		return ;
	}
	
	int mid=(l+r)/2;//中间值
	
	ms(a,l,mid);//分别继续拆分
	ms(a,mid+1,r);
	
	//STEP2
	int i=l,j=mid+1;//左右指针
	int k=l;//在l到r的数据中，b数组下标也是l到r
	
	//STEP3
	while(i<=mid&&j<=r)//只要指针没越界，就循环
	{
		if(a[i]<a[j])//按照分析进行
		{
			b[k]=a[i];
			i++,k++;
		}
		else
		{
			b[k]=a[j];
			j++,k++;
		}
	}
	
	//STEP4
	while(i<=mid)//两种情况都有可能
	{
		b[k]=a[i];
		i++,k++;
	}
	while(j<=r)
	{
		b[k]=a[j];
		j++,k++;
	}
	
	//STEP5
	for(int I=l;I<=r;I++)
	{
		a[I]=b[I];
	}
}

int n,m;

int main()
{
	cin>>n>>m;//两组的数据个数
	for(int i=1;i<=n;i++)
	{
		cin>>x[i];
	}
	for(int i=1;i<=m;i++)
	{
		cin>>y[i];
	}
	
	ms(x,1,n);//排序
	ms(y,1,m);
	
	int i=1,j=1;//按照归并的方法，将两组数组看做左右数据集
	int k=1;
	while(i<=n&&j<=m)
	{
		if(x[i]<y[j])
		{
			b[k]=x[i];
			i++,k++;
		}
		else
		{				
			b[k]=y[j];
			j++,k++;
		}
	}
	while(i<=n)
	{
		b[k]=x[i];
		i++,k++;
	}	
	while(j<=m)
	{
		b[k]=y[j];
		j++,k++;
	}
	
	for(int i=1;i<=n+m;i++)//输出
	{
		cout<<b[i]<<" ";
	}
	
	return 0;
}

有什么比上面的代码更简单的吗，有！因为最终都是要排成一组，所以我们是不是可以在输入的时候直接输入在一起，再统一排序，然后输出呢？这样就大大减少了我们的码量。

总结

在开头说了，我也是才学归并。评价一下，归并排序其实也没有那么难，只要能理解归并是什么意思，在将其的排序步骤理清楚，就不难解出了。