递归模型总结二——归并排序

1.前言

对初学递归的人来说，递归无疑是很不好理解的，本系列旨在对常见算法中使用的递归做一定程度的解析，学习这些算法的同时，总结出其递归模型。以便于加深对递归的理解，同时，当我们掌握了多种递归模型。那无论何时需要使用递归解决问题，我们都能从已有的递归模型中得到一些启发。或者相似的场景使用的模型是一样时（类似于数学或物理中的建模，通过对具有某类特征的事物的分析，总结出其一般规律，以便应用到具有相同特征的情况中去），我们便能套用已有的模型使用，相信会很方便。

2.归并排序

1.算法理解

摘自百度百科

归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

简单来说就是将一个序列分成两个序列，将两个序列排好序后再按大小顺序合并回去，在归并排序里我们会将一个序列递归的分割，直至其某一个子序列被分成两个只含一个元素的子序列。因为其只含一个元素，所以我们可以认为他有序，也就不用排序了。递归结束，开始回升合并。

举个例子便于理解归并排序：
有如下数据需要排序：

{1，4，2，65，76，15，9，0，54，32}；

我们首先使用递归深度的将上述数据分割成不可分割的子序列，即每个序列只有一个数据。分割过程为：

先分割{1，4，2，65，76，15，9，0，54，32}，被分割为：
{1，4，2，65，76} {15，9，0，54，32}；
{1，4，2，65，76} 继续递归分割为{1，4，2}与{65，76}；
{1，4，2}继续分割为{1，4}与{2}；
{1，4}继续分割为{1}与{4}；

至此{1，4}序列变为了最小的不可再分的序列，递归开始回升返回，开始合并{1}，{4}为一个有序序列。合并后为{1，4}该函数返回，处理与{1，4}一起分割出来的另一个序列{2}，{2}为最小序列不用再分割返回与{1，4}合并成一个有序序列，为{1，2，4}，该层函数返回，递归处理与{1,4,2}一起分割出来的{65,76} ，则{65,76}被分割为{65}与{76}，递归回升合并{65}，{76}，返回后为{65，76}，然后{65，76}与{1，2，4}合并为一个有序序列{1，2，4，65，76}，函数返回处理 {15，9，0，54，32}，直至{15，9，0，54，32}被处理为{0，9，15，32，54}返回与{1，2，4，65，76}合并为{0,1,2,4,9,15,32,54,65,76}。自此函数结束。

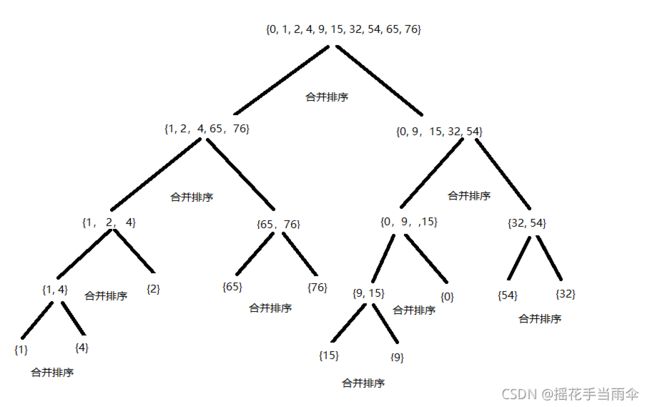
可能这样说还是不直观，看几张图以便理解：

接下来只剩一个点了，那就是合并有序序列的方法，其实这一步很简单：
举个例子：合并有序序列{1，2，4}与{65，76} 。首先从两个序列中各取出一个数分别为1与65，比较，1小，1先存入新的序列得{1} 。再从第一个序列取数为2，比较2小存入序列得{1，2} 。取4，比较，存入序列得{1，2，4} 。
此时第一个序列已经没有数据了。又因为序列都是有序的。所以只需第二个序列的数依次存入新序列就行了。

图1为递归调用的过程，图2为递归回升合并排序的过程。

2.代码

#include 
#include 
#include 
#include 

using namespace std;

int Sort(int* nums,int left,int mid,int right,int* tmp) {    //合并函数，创建一个临时数组，比较两个数组的元素大小，小的进入临时数组，直至两数组都为空

	int left_tmp = left;
	int mid_tmp = mid + 1;
	int count = 0;
	while (left_tmp <= mid && mid_tmp <= right) {      //将其中一个数组的元素全部存入临时数组

		if (nums[left_tmp] < nums[mid_tmp]) {
			tmp[count++] = nums[left_tmp++];
		}
		else {
			tmp[count++] = nums[mid_tmp++];
		}
	}

	while (left_tmp <= mid) {                    //再把另一个不为空的数组的元素全部存入数组中  
		tmp[count++] = nums[left_tmp++];
	}

	while (mid_tmp <= right) {                  //再把另一个不为空的数组的元素全部存入数组中  
		tmp[count++] = nums[mid_tmp++];
	}

	memcpy(nums + left, tmp, sizeof(int) * (right - left + 1));       //将临时数组中的元素全部存入nums数组

	return 1;
}


int mergeSort(int* nums, int left, int right, int* tmp) {

	if (left < right) {                      

		int mid = left + (right - left) / 2;
		mergeSort(nums, left, mid, tmp);            //递归拆分数组，直至数组中只有一个元素
		mergeSort(nums, mid + 1, right, tmp);
		Sort(nums, left, mid, right, tmp);          //合并数组
	}

	return 1;
}


int main(void) {

	int nums[10] = { 1,4,2,65,76,15,9,0,54,32 };
	//int nums[10] = { 1,4,2,6,7,15,9,0,5,33 };
	//int nums[10] = { 1,2,3,4,5,6,7,8,9,10 };

	int count = sizeof(nums) / sizeof(nums[0]);   //计算临时数组大小

	int* tmp = new int[count];                    //分配临时数组空间

	mergeSort(nums, 0, 9, tmp);

	for (auto& art : nums) {                      //打印nums元素
		cout << art << " ";
	}

	system("pause");

	return 0;
}

3.递归模型总结

        mergeSort(nums, left, mid, tmp);            
		mergeSort(nums, mid + 1, right, tmp);
		Sort(nums, left, mid, right, tmp); 

对递归的理解需要一些抽象思维，如果只在当前角度来看，不深入到递归的最底层。mergeSort(nums, left, mid, tmp)函数就可以看成一个排序函数，它会把nums数组从left到mid的元素从小到大排好序，mergeSort(nums, mid + 1, right, tmp)函数也一样将nums数组中从mid+1到right的数据排好序。两个函数都完成后，执行Sort(nums, left, mid, right, tmp)，即把两个已经有序的数组从小到大合并排序。实际上递归的每一层都是这样实现的。

归并排序其实是分治法的一个非常典型的应用，分治法算是递归的一类模型，它的特征是通过把原问题一分为二，直至其被分为我们想要的最小子问题（代码体现为：mergeSort(nums, left, mid, tmp) 与 mergeSort(nums, mid + 1, right, tmp)）。在归并排序中即原数组被分为只含一个元素的数组。然后递归回升，开始对分开的子序列进行我们想要的处理（代码体现为：Sort(nums, left, mid, right, tmp) ）。

其递归模型为先递归，直至两个递归回升，再对其进行某些我们需要的处理。从二叉树的角度来理解，就是后序遍历，先处理当前节点的左右节点，再输出当前节点的值。其实很多两路递归的结构都可以从二叉树的三种遍历中找到类似的思路结构。

再抽象一点结合代码理解就是由于分治法是一分为二，两路进行，所以递归函数里有两次递归，由于递归后往往要进行某些处理，所以还有进行处理的一步。还有一点值得注意的是：进行处理的一步未必是写在递归之后。还有可能是这样的：

        mergeSort(nums, left, mid, tmp);  
        Sort(nums, left, mid, right, tmp);          
		mergeSort(nums, mid + 1, right, tmp);
		

还可能是这样的：

        Sort(nums, left, mid, right, tmp);         
        mergeSort(nums, left, mid, tmp);   
		mergeSort(nums, mid + 1, right, tmp);

4.企业实战

1.问题：如果有一个100G的文件需要排序，但内存最大只能容纳1G的文件，那么怎么才能把文件里的数据排好序呢？

2.解决方法：我们可以使用类似归并排序的方法把100G的文件分成两个50G的文件，把50G的文件分成两个25G的文件，再继续细分下去，直至其被分成可在内存里操作的大小，将其在内存里排好序后写回文件中。比如我们最终把一个2G的文件细分为两个1G的文件，两个1G的文件在内存中排好序后写回到文件中，得到了两个排好序的1G文件，再使用我们在归并排序中使用的排序方法就能1G的内存中排好两个1G的文件得到一个2G的文件（实际上此时排序10MB的内存都够了，因为我每次只需要取出两个数比较大小再存入文件就行了。每次只需要两个数的空间）。以此类推，再大的文件都可以排好序。