前缀和详解

写在前面

不要再硬套模板了，来看看这些细节是否注意到了！

一维前缀和

1. 一维前缀和的构造原理

先来看看前缀和常见的题目问法：

输入一个长度为n的整数序列。接下来再输入m个请求，每个请求输入一对 l, r。对于每个请求，输出原序列中从第 l 个数到第 r 个数的和。

思考一下，我们很容易想出暴力解法，循环遍历区间求和。这样时间复杂度就是O(m * n)，那么如果使用前缀和算法就可以将时间复杂度降为O(m + n)，代价就是额外创建一个数组，典型的以空间换时间问题！

while(m--)
{
    for(int i = l; i <= r; i++)
    { 
        sum += a[i];
    }
}

一维前缀和构造 细节处理

这里会有两种常见的情况，具体使用哪种方式，根据实际题目要求来决定！

1. 一种情况就是在构造前缀和数组的同时，直接输入；当然也可以先存进数组中，再构造前缀和数组，这两种方式的实现如下：

// 方式1
// 前缀和的构造
for(int i = 1; i <= n; i++)
{
    int x;
    cin >> x;
    S[i] = S[i - 1] + x;
}

// 方式2
// 填充一维数组
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

// 构造前缀和数组
for (int i = 1; i <= n; i ++ ) S[i] = S[i - 1] + a[i]; 

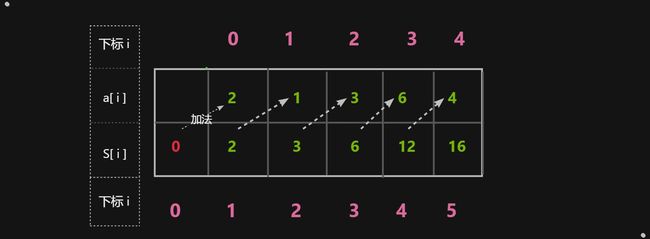
如图，上面的数组是要查询的原数组，下面的数组是我们要构造的前缀和数组
两种数组都是从第二个位置存取数据的，这样做有其好处，在进行加法运算时不至于数组越界

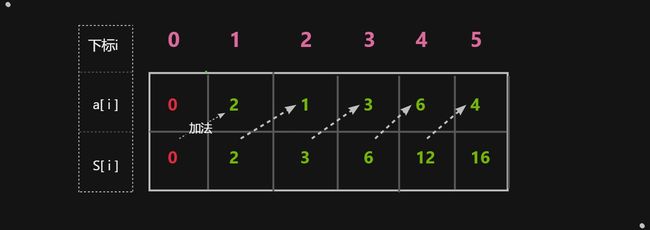
2. 还会遇到像leetcode题中直接给好整数数组，这时，整数一般都是从a[ 0 ]开始存取的，就得对上面的处理方式做一些小改动：

// 构造前缀和数组
for (int i = 1; i < n; i++)
    S[i] = S[i - 1] + a[i - 1];

2. 一维前缀和查询原理

cout << S[right] - S[left - 1];

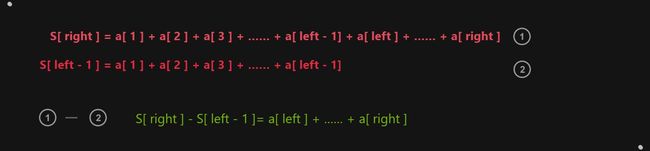
1. 当输入要求的区间值的左右端left和right时（这里不是下标，而是下标+1），使用上面的公式就可以计算出区间的值的和了，原理可以用高中所学的数列知识来验证：

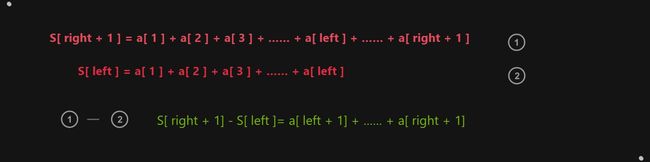
2. 当这里的left和right值是下标时，对应的查询操作也要少许改动

cout << S[right + 1] - S[left];

3. 一维前缀和的应用

AcWing 795. 前缀和

题目描述
输入一个长度为 n 的整数序列。 接下来再输入 m 个询问，每个询问输入一对 l，r。 对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。 第二行包含 n 个整数，表示整数数列。 接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。
输出格式
共 m 行，每行输出一个询问的结果。
数据范围
1≤l≤r≤n， 1≤n,m≤100000， −1000≤数列中元素的值≤1000
输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10

#include 
using namespace std;

int main()
{
    int m, n;
    int S[100000] = {0};
    int l, r;
    cin >> n >> m;

    // 前缀和的构造
    for(int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        S[i] = S[i - 1] + x;
    }

    // 前缀和的查询
    while(m --)
    {
        cin >> l >> r;

        cout << S[r] - S[l - 1] << endl;
    }
    return 0;
}

leetcode 303. 区域和检索 - 数组不可变

class NumArray {
public:

    // 前缀和数组
    vector<int> S;

    NumArray(vector<int>& nums) {

        int n = nums.size();
        S.resize(n + 1);
        //构造前缀和
        for(int i = 1; i < S.size(); i++)
            S[i] += S[i - 1] + nums[i - 1];
    }
    
    // 查询前缀和
    int sumRange(int left, int right) {
        return S[right + 1] - S[left];
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(left,right);
 */

---

二维前缀和

那么我们再扩展一下，将原来的一维数组扩展到二维成为矩阵，前缀和思想依然能够解决

输入一个 n 行 m 列的整数矩阵，再输入q个查询，每个查询包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个查询输出子矩阵中所有数的和。

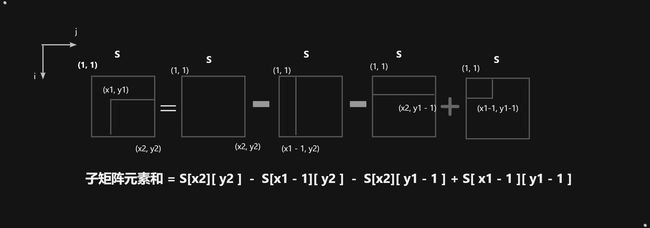
很明显，我们了解到题目的用意：求子矩阵的元素和，实际上任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和。

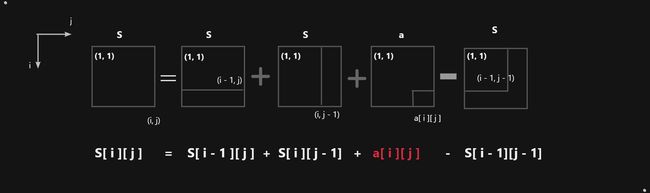
1. 二维前缀和构造原理

1. 假如我们从a[ ][ ]数组的(1, 1)为原点开始，另构造一个前缀和数组S[ ] [ ]，经过一次循环遍历之后，这个前缀和矩阵内第(i, j)个位置存取的就是以(1, 1)和(i, j)构成的矩形的元素和。

2. 假如我们以从a[ ][ ]数组的(0, 0)为原点开始，另构造一个前缀和数组S[ ] [ ]，计算方式和上面基本相同

2. 二维前缀和查询原理

1. 查询的时候也是有小细节的，如果题目中给出的(x1, y1, x2, y2)是元素所在的位置（下标值+1）

S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

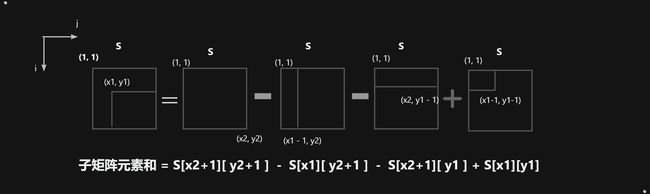
2. 如果题目给出的(x1, y1, x2, y2)是下标，那么只需要小小的改动即可

S[x2+1][y2+1] - S[x1][y2+1] - S[x2+1][y1] + S[x1][y1];

3. 二维前缀和的应用

下面是在各个平台搜集的题目，来练练手吧！

AcWing 796.子矩阵的和

题目描述
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。 对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n，m，q 接下来 n 行，每行包含 m 个整数，表示整数矩阵。 接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。
输出格式
共 q 行，每行输出一个询问的结果。
数据范围
1≤n,m≤1000 1≤q≤200000 1≤x1≤x2≤n 1≤y1≤y2≤m −1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17 27 21

#include 
using namespace std;

int n, m, q;
int a[1010][1010];
int S[1010][1010];
int  x1, y1, x2, y2;

int main()
{

    cin >> n >> m >> q;

    // 前缀和的构造
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin >> a[i][j];
            S[i][j] = S[i - 1][j] + S[i][j - 1] + a[i][j]- S[i - 1][j - 1];
        }
    }

    // 前缀和的查询
    while(q--)
    {
        cin >>  x1 >> y1 >> x2 >> y2;
        cout << S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1] << endl;
    }

    return 0;
}

leetcode 304.二维区域和检索 - 矩阵不可变

class NumMatrix {
public:
    vector< vector<int> > S; 

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        
        S = vector<vector<int>>(m + 1, vector<int>(n + 1, 0));
        for(int i = 1; i <= m; i++)
            for(int j = 1; j <= n; j++)
            // 构造前缀和矩阵
                S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + matrix[i - 1][j - 1]; 
    }
    
    int sumRegion(int x1, int y1, int x2, int y2) {
        return S[x2+1][y2+1] - S[x1][y2+1] - S[x2+1][y1] + S[x1][y1];
    }
};

leetcode LCR 013.二维区域和检索 - 矩阵不可变

class NumMatrix {
public:
    vector<vector<int>> S;
    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        /*vector(n + 1, 0)
        这部分代码表示创建一个大小为(n + 1)的一维向量，并将所有元素初始化为0
        */
        S = vector<vector<int>>(m + 1, vector<int>(n + 1, 0));
        for(int i = 1; i <= m; i++)
            for(int j = 1; j <= n; j++)
                S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + matrix[i-1][j-1];
    }
    
    int sumRegion(int x1, int y1, int x2, int y2) {
        return S[x2+1][y2+1] - S[x1][y2+1] - S[x2+1][y1] + S[x1][y1];
    }
};

写在最后

点赞，你的认可是我创作的动力！
⭐收藏，你的青睐是我努力的方向！
✏️评论，你的意见是我进步的财富！