从零开始的强化学习笔记1（结合书本与网上的多篇资料总结）

当我打开一个机械臂的强化学习教程：

让我们从零开始做一个机械手臂(强化学习) - 知乎 (zhihu.com)

发现其中使用了DDPG算法。由于没学习过DDPG，于是我打开了DDPG教程：

一文带你理清DDPG算法（附代码及代码解释） - 知乎 (zhihu.com)

发现作者建议我先去了解DQN算法，于是我打开一篇DQN教程：

三维可视化助你直观理解DQN算法[DQN理论篇] - 知乎 (zhihu.com)

文章表示DQN延续了一部分Qlearning的思路。于是我打开一篇Qlearning教程：

[理论篇]怎样直观理解Qlearning算法？ - 知乎 (zhihu.com)

Qlearning中使用TD估算状态价值。什么是TD？

如何用时序差分TD估算状态V值？ - 知乎 (zhihu.com)

TD是对蒙地卡罗(MC)算法的改进：

如何用蒙地卡罗方法（Monte-Carlo）估算V值？ - 知乎 (zhihu.com)

还是要从基础学起。

马尔可夫决策过程

首先是马尔可夫决策过程，这里可理解为一个由原状态、动作和目标状态组成的三维矩阵：

当你处于一个源状态i时，就处于上图立方体中的一个面。将平面理解为如下的表格：

       执行不同的动作，转换到下一个状态的概率也不同，转换到不同状态时所获得的奖励也不同。执行动作的概率则是由智能体的策略决定的。这就是强化学习的目标———找到获得奖励最大的最佳策略（也可以理解为训练智能体的最终目的）。

       这里插一嘴，智能体可以通过选择不同的动作来决定下一状态的概率。但是一个动作对应的转换下一状态的概率是固定的，及采取动作A后转换到状态J、K、E、F、G的概率固定是0.1、0.1、0.5、0.1、0.2，这是由智能体所处的环境决定的（若要模拟具有丰富观察的复杂现实环境，其环境函数的建立非常困难，因此基于模型的方法往往用于确定性环境，例如有严格规则的棋盘游戏），但事实上我们并无法直接定义概率，而要通过智能体一次次地重复训练来获得数据，估计出合理的概率。这里涉及到后面对Q值和V值的估计。

Env函数

      再顺便提一嘴，在强化学习库OpenAI Gym中。其环境类函数Env一般包含四个函数：

      action_space：可执行动作的集合

      observation_space：观察结果的集合

      reset()：重置环境

      step()：执行动作并返回其带来的后果信息。一般包含以下几项：

第一项是step()传递的参数（动作）。如step(0)表示执行动作0。

第二项observation表示执行完动作0后到达下一个状态，在此状态获得环境的新观察结果。

第三项reward表示这次动作收获的奖励。

第四项done是布尔指示符，表示episode是否结束（结束时为True）。

       下一步，如何让智能体收获的奖励最大化？

       首先要考虑未来。不能因为下一步执行动作A奖励最大就坚定的选择动作A。有可能A导致的新状态下执行所有动作都会扣奖励，那么回头去看动作A并不是最好的选择。最好能综合考虑未来的奖励收益来选择动作。

       不能一次到达终点后就不再尝试，应多次尝试找到奖励最大的路径。

Q值和V值

这里引入新概念：Q值和V值。可以看一下教程：如何理解强化学习中的Q值和V值？ - 知乎 (zhihu.com)

划重点：评估动作的价值，我们称为Q值：它代表了智能体选择这个动作后，一直到最终状态奖励总和的期望； - 评估状态的价值，我们称为V值：它代表了智能体在这个状态下，一直到最终状态的奖励总和的期望。

V值会根据不同的策略产生变化！（1）

与V值不同，Q值和策略并没有直接相关，而与环境的状态转移概率相关，而环境的状态转移概率是不变的。

一个状态的V值，就是这个状态下的所有动作的Q值，在策略下的期望。

折扣率 在强化学习中，有某些参数是人为主观制定。这些参数并不能推导，但在实际应用中却能解决问题，所以我们称这些参数为超参数，而折扣率就是一个超参数。 与金融产品说的贴现率是类似的。我们计算Q值，目的就是把未来很多步奖励，折算到当前节点。但未来n步的奖励的10点奖励，与当前的10点奖励是否完全等价呢？未必。所以我们人为地给未来的奖励一定的折扣，例如：0.9,0.8，然后在计算到当前的Q值。

蒙地卡罗(MC)和时序差分(TD)

那么如何计算每个状态节点和动作节点的价值呢？这里有两个方法：蒙地卡罗(MC)和时序差分(TD)。

蒙地卡罗算法可以理解为：智能体从某一个状态出发，经过多个状态后到达最终状态，这一路上记下每次的状态转移以及获得的奖励R。然后原路返回，在途经的每一个状态上标记这个状态的G值，G等于遇上一个状态的G值乘以一定的折扣再加上奖励r。智能体多次训练后，会经过同一个状态多次，而每次标记的该状态的G值是不一样的，取一个平均数，就是该状态的V值。

蒙地卡罗是基于无模型的算法，因为他不需要知道整个环境的模型，只需要一个劲的往前走就是了。

G值的意义在于某个状态到最终状态的奖励总和。策略不同，同一个状态的V值也会不同（1）。

蒙地卡罗的缺点在于，每次实验都需要智能体从最初状态到最终状态完整的走一遍。但如果状态空间非常大，有上万个状态，蒙地卡罗会浪费很多时间，计算量过大。这里就需要时序差分（TD）法了。

时序差分法可以理解为走一步看一步。将新状态当成最终状态，然后回过头去更新上一状态的V值。这一点可以从公式中看出区别。蒙地卡罗的更新公式：

时序差分法的更新公式如下：

      可以看出蒙地卡罗需要这一时刻返回的G值（智能体已走完全程，原路返回到此状态时计算出的G值），而时序差分法只需要到下一状态时获得的回报Rt+1，也就是把状态t到状态t+1这一过程的回报当作G值，也就是把下一状态当最最终状态！然后每次到一个新的状态就回过头去更新所有之前状态的V值！

Qlearning 和 SARSA

       以上两个算法都是用来估计状态节点的V值，为何不直接估算动作节点的Q值？本就是要让智能体选择奖励最大的动作。但是估算Q值还需要估算下一个状态的Vt+1值，这就非常麻烦了，能不能找到一个Q值来代替下一状态的Vt+1值?这里给出了两种替代方案：QLearning和SARSA。

SARSA用动作的Q值代替Vt+1。这里的动作是基于策略选取的，即依据策略的动作概率随机选取某一个动作。但既然我们的目标是让智能体获得最大的收益，为何不直接选取Q值最大的动作？这就是Qlearning的思路，直接选取Q值最大的那个动作的Q值来代替Vt+1。这两个方法之间就差一个Max。

深度强化学习（DQN、PG、Actor-Critic、PPO、DDPG）

到这里就出现了一个问题。智能体在训练过程中需要计算每个状态S和该状态在不同行为下所拥有的Q值，将这些信息以表格的方式存储起来。这种方式适用于离散型的状态问题，当面对连续型问题的时候，状态与动作的数量过大，用于存储的表格就会非常大，非常消耗计算机的内存。

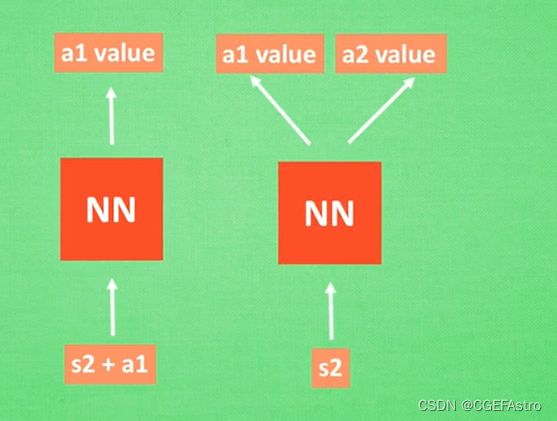
而神经网络，则非常适用于处理连续型状态问题，即线性回归（Linear Regression）。可以将神经网络视为一个函数，我们将当前状态与执行的动作作为输入，神经网络则输出对这个动作的Q值的预测。或是当前状态作为输入，神经网络输出不同动作对应的Q值。这样就不需要一个巨大的表格去存储信息，只需通过神经网络的计算就可以。

       将神经网络引入QLearning算法，就得到了DQN算法——>Deep net Qlearning。这里开始就进入深度强化学习的领域了（深度学习与强化学习的结合）。

今天笔记先记到这里，欢迎大佬交流指导(ᕑᗢᓫ∗)˒

参考：

你有一份强化学习线路图，请查收。(原题：看我如何一文从马可洛夫怼到DPPO) - 知乎 (zhihu.com)

什么是 DQN | 莫烦Python (mofanpy.com)

什么是 Policy Gradients | 莫烦Python (mofanpy.com)

《深度强化学习入门与实践指南》——马克西姆·拉潘