二叉树带图详解

---

一、二叉树的特点

• 每个结点最多有两颗子树
• 左子树和右子树是有顺序的
• 即使树中某结点只有一颗子树，也要区分它是左子树还是右子树

二叉树有以下五种基本形态：

二、特殊二叉树

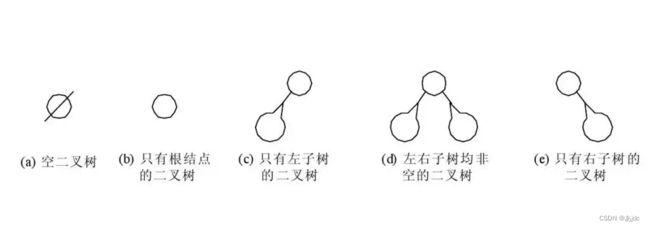
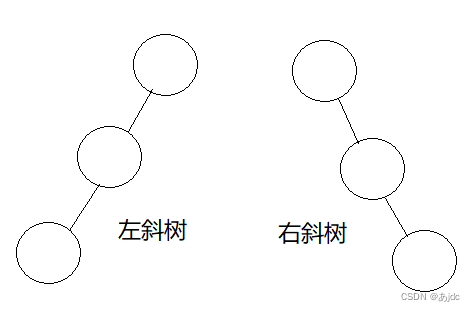
1.斜树

所有的结点都只有左子树的二叉树叫左斜树，所有结点都只有右子树的二叉树叫右斜树。

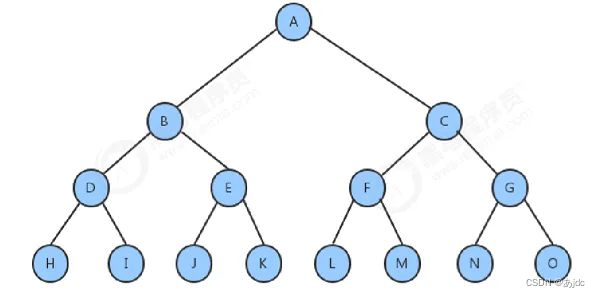
2.满二叉树

在一颗二叉树中，如果所有结点分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

满二叉树的特点有：
（1）叶子只能出现在最下一层。出现在其他层就不可能达到平衡。
（2）非叶子结点的度一定是2。否则就是“缺胳膊少腿了”。
（3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

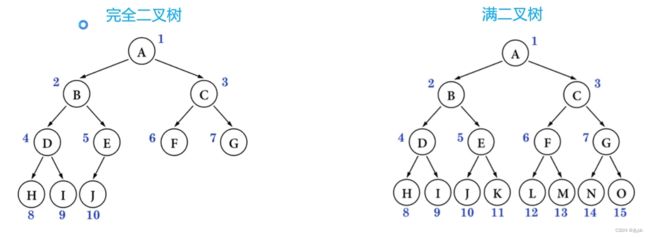
3.完全二叉树

对一颗具有n个结点的二叉树按层序编号，如果编号为i的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

完全二叉树的特点：
（1）叶子结点只能出现在最下两层。
（2）最下层的叶子一定集中在左部连续位置。
（3）倒数第二层，若有叶子结点，一定都在右部连续位置。
（4）如果结点度为1，则该结点只有左孩子。
（5）同样结点数为2的二叉树，完全二叉树的深度最小。

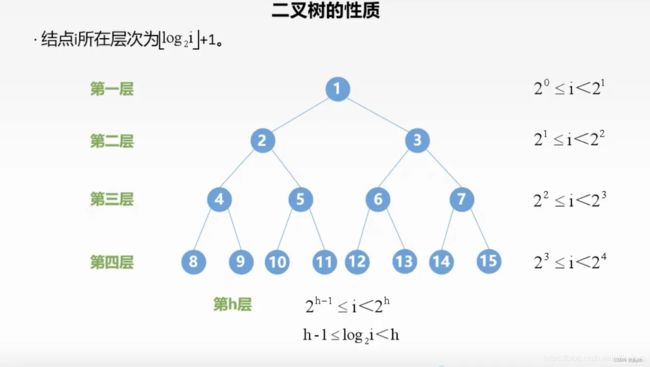
三、二叉树的性质

性质1：在二叉树的第i层最多有2^i-1个结点。
性质2：深度为k的二叉树最多有2^k-1个结点。
性质3：对任意一颗二叉树，如果其终端结点数为n₀，度为2的结点数为n₂，则n₀= n₂+1。
性质4：具有n个结点的完全二叉树的深度为 log₂n+1。
性质5：如果根节点标号为1，则对任意结点i，它的左孩子为2i，右孩子为2i+1。

四、二叉树的遍历等操作

1、前序遍历

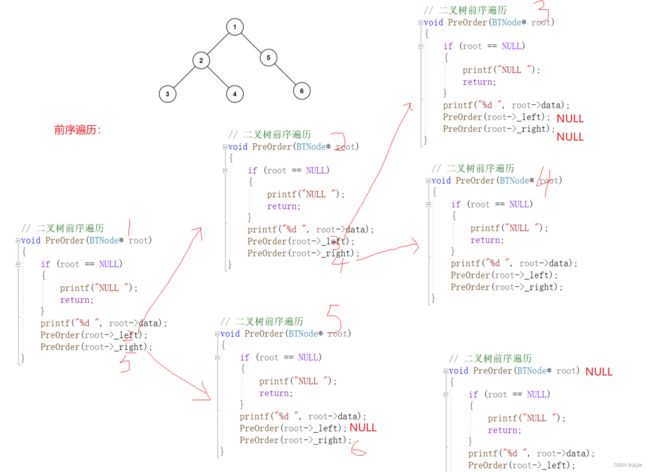
规则是若二叉树为空，则空操作返回，否则先访问根节点，然后前序遍历左子树，在前序遍历右子树。如下图的遍历顺序为1 2 3 NULL NULL 4 NULL NULL 5 NULL 6 NULL NULL（我们在遍历时把空也加上，避免我们误以为没有访问空结点）。

前序遍历的代码如下：

// 二叉树前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->_left);
	PreOrder(root->_right);
}

我们可以观察到，我们的代码采用了递归，但理解递归的最好方式是画递归展开图，所以我们绘制如下展开图，来帮助我们理解。

2、中序遍历

规则是若树为空，则空操作返回，否则从根节点开始（并不是先访问跟结点），中序遍历跟结点的左子树，然后是访问跟结点，最后中序遍历右子树。如下图的遍历顺序为：NULL 3 NULL 2 NULL 4 NULL 1 NULL 5 NULL 6 NULL

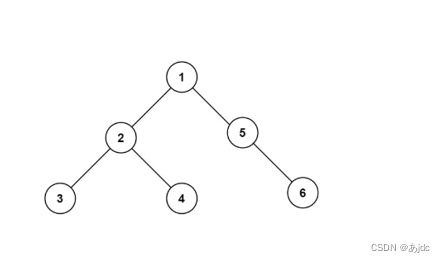
中序遍历的代码如下：

// 二叉树中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->_left);
	printf("%d ", root->data);
	InOrder(root->_right);

}

3、后序遍历

规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根节点。如下图的遍历顺序为：NULL NULL 3 NULL NULL 4 2 NULL NULL NULL 6 5 1。

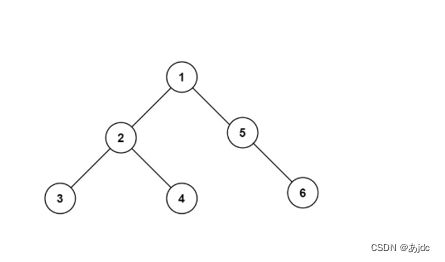
后序遍历的代码如下：

// 二叉树后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->_left);
	PostOrder(root->_right);
	printf("%d ", root->data);

}

4、二叉树结点的个数

我们同样可以采用递归的思想，遍历每一颗子树的每一个结点。

我们访问到空结点时，返回0，那么这个空结点的父亲结点返回1，然后层层向上返回，左子树的结点加上右子树的结点，最后再加上跟结点，便是二叉树结点的个数。

//求结点个数
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->_left) + TreeSize(root->_right) + 1;
}

5、叶子结点的个数

叶子结点的特征是左右子树为空，所以我们同样可以通过递归的方法遍历每一颗子树。

终止条件是根节点为空，叶子结点的条件是左右子树为空，我们得到左右子树中叶子结点的个数然后返回即可。

//求叶子结点个数
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	//叶子结点的特征是左右为空
	if (root->_left == NULL && root->_right == NULL)
		return 1;

	return TreeLeafSize(root->_left) + TreeLeafSize(root->_right);

}

6、树的深度

树的深度是求最大深度，所以我们需要遍历左右子树，然后进行比较，选出较大值返回。

我们遍历时，需要有两个值来分别计数左右子树的深度，然后返回较大值。

//求树的深度
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	
	int left = TreeHeight(root->_left);
	int right = TreeHeight(root->_right);

	return ( left > right ? left  : right ) + 1;
}

7、第k层结点的个数

第一层结点就是根节点，个数为1，然后向下访问k-1层，直到k等于1。

注意返回值是左右子树的和。

//求树第k层结点的个数
int TreeLevelkSize(BTNode* root , int k)
{
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return TreeLevelkSize(root->_left, k - 1) + TreeLevelkSize(root->_right, k - 1);
}

8、查找树中的某个值

我们可以先查找左子树，如果没有找到返回，继续查找右子树，如果没有找到则返回空。

注意我们需要判断根节点是否是我们查找的结点。

//查找树中某个结点
BTNode* FindNode(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->data == x)
		return root;

	if (FindNode(root->_left, x))
		return FindNode(root->_left, x);
	else
		return FindNode(root->_right, x);
}

总结

对于树的操作，我们常采用递归的方法，多画图可以帮助我们更好的理解树。