机器学习(3) 一元线性回归(最小二乘法实现)
一元线性回归是分析只有一个自变量x 和 因变量y 线性相关关系的方法。一个经济指标的数值往往受许多因素影响,若其中只有一个因素是主要的,起决定性作用,则可用一元线性回归进行预测分析。
一元线性回归分析预测法,是根据自变量x和因变量Y的相关关系,建立x与Y的线性回归方程进行预测的方法。由于市场现象一般是受多种因素的影响,而并不是仅仅受一个因素的影响。所以应用一元线性回归分析预测法,必须对影响市场现象的多种因素做全面分析。只有当诸多的影响因素中,确实存在一个对因变量影响作用明显高于其他因素的变量,才能将它作为自变量,应用一元相关回归分析市场预测法进行预测。
1 【Octave】实现一个地区的房价预测
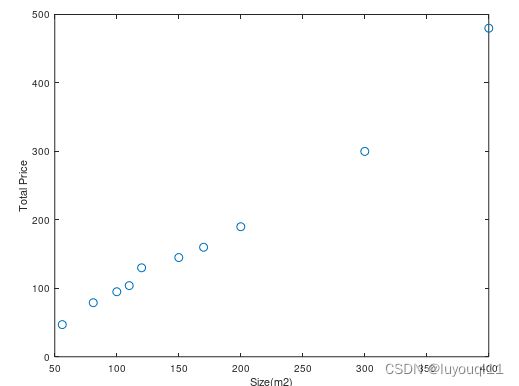
已知某一地区卖出10套房子,这10套房子的面积和总价分别为
| 面积( |
56 |
81 |
100 |
110 |
120 |
150 |
170 |
200 |
300 |
400 |
| 总价(万元) |
47 |
79 |
95 |
104 |
130 |
145 |
160 |
190 |
300 |
480 |
预测房屋面积为90平方米时的房价。
第一步:绘制样本图
根据样本绘制,其总价——面积图为:
第二步:选择拟合曲线,并绘制拟合曲线图
根据样本,我们选择Y=aX+b的拟合曲线,如下:
第三步:根据拟合曲线预测房价,并在图上标识出来
拟合曲线为Y=1.191X-27.9166
取X=[77,230,420],根据拟合曲线,则有Y=[ 63.788,246.006,472.291]
以上就是整个模型、拟合、预测的整个过程。
在Octave中的脚本area_value.m
close all;clc;clear;
% 样本数据
x=[56,81,100,110,120,150,170,200,300,400]; %房屋面积
y=[47,79,95,104,130,145,160,190,300,480];% 第一步:绘制样本数据
fprintf('绘制样本数据 ...\n')
plot(x,y,'o'); % 标记所有样本
xlabel('Size(m2)');ylabel('Total Price'); % 设置坐标区Axes的x,y轴标签fprintf('样本绘制完成. Press enter to continue.\n');
pause;% 第二步:拟合曲线
% 拟合一次曲线y=ax+b
p1=polyfit(x,y,1)
% 绘制拟合曲线
x1=0:1:500; % 起始值为0,增量为1,结束值为500
y1=polyval(p1,x1); % 求拟合曲线对应的值
plot(x,y,'o',x1,y1); % 标记样本、绘制预测曲线
title('y=ax+b'); % 设置坐标区Axes的标题
grid on % 给坐标区Axes增加网格。
xlabel('Size(m2)');ylabel('Total Price'); % 设置坐标区Axes的x,y轴标签fprintf('预测曲线绘制完成. Press enter to continue.\n');
pause;% 第三步:根据预测曲线预测房价
i=[77,230,420]; % 给出假定的房屋面积值
j=polyval(p1,i); % 预测房价
hold on; % 保持图形不变
plot(i,j,'pr'); % 绘出预测值
完善的脚本area_value.m
上面的样本采用了线性拟合,对同样的样本,可以采用不同的拟合曲线(一元二次、一元三次、一元四次等等)。
完善在Octave中的脚本area_value.m如下:
close all;clc;clear;
% 样本数据
x=[56,81,100,110,120,150,170,200,300,400]; %房屋面积
y=[47,79,95,104,130,145,160,190,300,480];% 第一步:绘制样本数据
fprintf('绘制样本数据 ...\n')
plot(x,y,'o'); % 标记所有样本
xlabel('Size(m2)');ylabel('Total Price'); % 设置坐标区Axes的x,y轴标签fprintf('样本绘制完成. Press enter to continue.\n');
pause;% 第二步:拟合曲线
% 最小二乘法拟合一次曲线y=ax+b
p1=polyfit(x,y,1)
% 绘制拟合曲线
x1=0:1:500; % 起始值为0,增量为1,结束值为500
y1=polyval(p1,x1); % 求拟合曲线对应的值
plot(x,y,'o',x1,y1); % 标记样本、绘制预测曲线
title('y=ax+b'); % 设置坐标区Axes的标题
grid on % 给坐标区Axes增加网格。
xlabel('Size(m2)');ylabel('Total Price'); % 设置坐标区Axes的x,y轴标签fprintf('预测曲线绘制完成. Press enter to continue.\n');
pause;% 第三步:根据预测曲线预测房价
i=[77,230,420]; % 给出假定的房屋面积值
j=polyval(p1,i); % 预测房价
hold on; % 保持图形不变
plot(i,j,'pr'); % 绘出预测值
fprintf('根据预测曲线预测房价完成. Press enter to continue.\n');
pause;% 第四步:选择不同的拟合曲线并绘制出来
% 算出2、3,4次拟合曲线,并绘制出来
p2=polyfit(x,y,2); % 一元二次曲线
p3=polyfit(x,y,3); % 一元三次曲线
p4=polyfit(x,y,4); % 一元四次曲线
y2=polyval(p2,x1);
y3=polyval(p3,x1);
y4=polyval(p4,x1);
hold on; % 保持图形不变
plot(x1,y2,'y',x1,y3,'g',x1,y4,'b'); % 绘制2、3、4次曲线
legend('Sample','Linear','Forecast','Quadratic','Cubic','Quartic');
最终结果如下:
2 【python】实现学习时长和学习成绩的预测
## 一元线性回归
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas import DataFrame,Series
from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegressionplt.rcParams['font.sans-serif'] = ['SimHei']
# 1、创建数据集
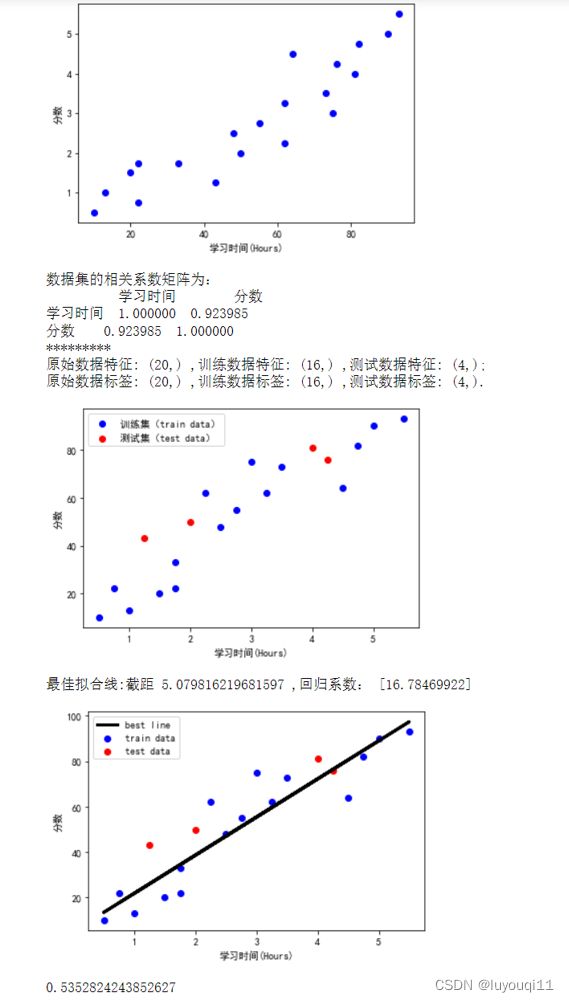
examDict = {'学习时间':[0.50,0.75,1.00,1.25,1.50,1.75,1.75,
2.00,2.25,2.50,2.75,3.00,3.25,3.50,4.00,4.25,4.50,4.75,5.00,5.50],
'分数':[10,22,13,43,20,22,33,50,62,
48,55,75,62,73,81,76,64,82,90,93]}
# 1.1 转换为DataFrame的数据格式
examDf = DataFrame(examDict)
print(examDf)
# 1.2 绘制训练集的散点图
plt.scatter(examDf.分数,examDf.学习时间,color = 'b',label = "Exam Data")
# 1.2.1 添加图的标签(x轴,y轴)
plt.xlabel("学习时间(Hours)")
plt.ylabel("分数")
# 1.2.2 保存数据集的散点图,并显示图像
plt.savefig("examDf.jpg")
plt.show()
# 1.3 计算数据集的相关系数矩阵
# 相关系数矩阵 r(相关系数) = x和y的协方差/(x的标准差*y的标准差) == cov(x,y)/σx*σy
# 相关系数0~0.3弱相关0.3~0.6中等程度相关0.6~1强相关
rDf = examDf.corr()
print("数据集的相关系数矩阵为:")
print(rDf)
print('*********')
# 2 将原数据集拆分训练集和测试集
exam_X = examDf.loc[:,'学习时间']
exam_Y = examDf.loc[:,'分数']
X_train,X_test,Y_train,Y_test = train_test_split(exam_X,exam_Y,train_size=.8)
# X_train为训练数据标签,# X_test为测试数据标签,
# exam_X为样本特征
# exam_y为样本标签,
# train_size 训练数据占比
print(f'原始数据特征: {exam_X.shape} ,训练数据特征: {X_train.shape} ,测试数据特征: {X_test.shape};')
print(f'原始数据标签: {exam_Y.shape} ,训练数据标签: {Y_train.shape} ,测试数据标签: {Y_test.shape}.')
# 2.1 绘制训练集和测试集散点图
plt.scatter(X_train, Y_train, color="blue", label="训练集(train data)")
plt.scatter(X_test, Y_test, color="red", label="测试集(test data)")
# 2.2 添加图标标签
plt.legend(loc=2)
plt.xlabel("学习时间(Hours)")
plt.ylabel("分数")
#显示图像
plt.savefig("tests.jpg")
plt.show()
# 3 一元线性回归
# 回归方程 y = a + b*x (模型建立最佳拟合线)
# 点误差 = 实际值 - 拟合值
# 误差平方和(Sum of square error) SSE = Σ(实际值-预测值)^2
# 最小二乘法 : 使得误差平方和最小(最佳拟合)# 3.1 数据预处理
# 对于下面的模型错误我们需要把我们的训练集进行reshape操作来达到函数所需要的要求
# model.fit(X_train,Y_train)
#reshape如果行数=-1的话可以使我们的数组所改的列数自动按照数组的大小形成新的数组
#因为model需要二维的数组来进行拟合但是这里只有一个特征所以需要reshape来转换为二维数组
X_train = X_train.values.reshape(-1,1)
X_test = X_test.values.reshape(-1,1)
# 3.2 调用线性回归API
model = LinearRegression()
# 3.3 求优化参数
model.fit(X_train,Y_train)
a = model.intercept_#截距
b = model.coef_#回归系数
print("最佳拟合线:截距",a,",回归系数:",b)
#R方检测
#对于评估模型的精确度
#y误差平方和 = Σ(y实际值 - y预测值)^2
#y的总波动 = Σ(y实际值 - y平均值)^2
#有多少百分比的y波动没有被回归拟合线所描述 = SSE/总波动
#有多少百分比的y波动被回归线描述 = 1 - SSE/总波动 = 决定系数R平方
#对于决定系数R平方来说1) 回归线拟合程度:有多少百分比的y波动刻印有回归线来描述(x的波动变化)
#2)值大小:R平方越高,回归模型越精确(取值范围0~1),1无误差,0无法完成拟合
# 3.4 绘制训练集离散图
plt.scatter(X_train, Y_train, color='blue', label="train data")
# 3.5 训练数据的预测值
y_train_pred = model.predict(X_train)
# 3.6 绘制最佳拟合线:标签用的是训练数据的预测值y_train_pred
plt.plot(X_train, y_train_pred, color='black', linewidth=3, label="best line")
# 3.7 测试数据散点图
plt.scatter(X_test, Y_test, color='red', label="test data")
# 3.8 添加图标标签
plt.legend(loc=2)
plt.xlabel("学习时间(Hours)")
plt.ylabel("分数")
# 3.9 显示图像
plt.savefig("lines.jpg")
plt.show()
score = model.score(X_test,Y_test)
print(score)
在jupyter notebook中,运行结果如下: