数据结构之优先级队列(堆)
文章目录
- 一、优先级队列介绍
- 二、优先级队列的模拟实现
-
- (1)堆的存储分析
- (2)创建堆的思路分析
- (3)代码实现操作
一、优先级队列介绍
1.概念: 在我们平时系统的操作中,有些情况下会存在对问题处理的先后顺序,所以数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。
PriorityQueue底层使用了堆的数据结构,所谓堆,就是一棵比较特殊的二叉树,完全二叉树,在这个基础上实现的结构就叫作堆。
二、优先级队列的模拟实现
(1)堆的存储分析
1.堆的存储方式:大根堆存储,小根堆存储。
小根堆:根节点总是比左右子节点小。
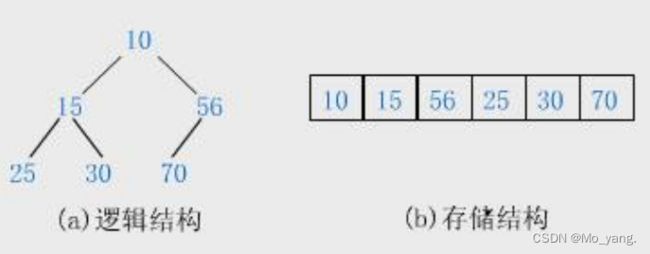
大根堆:根节点总是比左右子节点大。
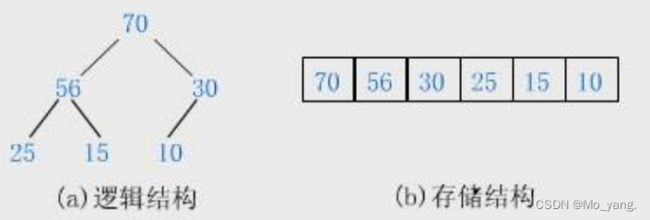
2.堆采用的存储是以层序存储的方式进行,存储在数组当中。
将元素存储到数组后,在以实现树的方式对堆进行实现。
设 i 结点为数组中的下标,则有以下特点:
(1). 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2。
(2). 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子。
(3). 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子。
(2)创建堆的思路分析
这里,我们以集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据,将其创建成堆。


如上图,这些元素的存储方式,是以数组的方式存储的,在逻辑上,我们以顺序排序的方式将元素,以数组下标为基础实现成一棵二叉树。
这里以大根堆为例进行实现:
实现思路:
我们已经了解了,大根堆的特点是根节点的元素始终比左右子树都要大,那么,很明显,要调整这棵树,是需要将较小的根的从上面下降至下面,简称就是,向下调整。这里,就需要定义两个变量,一个找到最后一个数组元素即 child 结点,另一个则要找到这个结点的父节点即 parent 结点。
大致操作如下图,以 第一次调整 数字 37 为例实现:
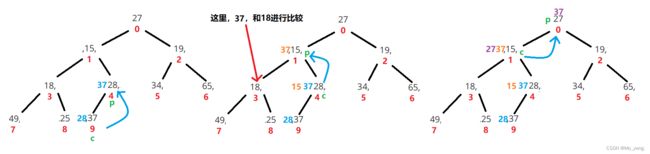
在我们自主实现优先级队列时,我们,除了首先将元素排列有序,我们还有实现下面几种操作:
即,插入和删除。
(3)代码实现操作
1.我们先实现将上面元素构成为大根堆的代码:
首先实现基本操作
//这些基本的数据存储在数组中
public int[] elem;
public int usedSize;
//定义一个初始给定数组长度的元素
public static final int DEFAULT_SIZE = 10;
public MyPriorityQueue(){
elem = new int[DEFAULT_SIZE];
}
//这里实现一个将数组元素从测试类中传递到当前数组中
public void intElem(int[] array){
for(int i; i < array.length; i++){
elem[i] = array[i];
usedSize++;
}
}
这里实现创建堆方法和向下调整
//实现创建堆方法
public void createHeap(){
//这里,我们需要知道如何找到parent结点
//如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2。
for(int parent = (usedSize -1 -1)/2; parent >= 0; parent--){
//这里就需要调用向下调整的方法
shiftDown(parent,usedSize);
}
}
//这里的len 表示数组现在真题的长度。
//这里的parent 表示找到的父亲结点。
private void shiftDown(int parent,int len){
//这里需要找到对应的孩子结点,需要知道:
//child = parent*2+1
int child = parent*2 + 1;
//这个方法找到的是左孩子,所以我们需要确定右孩子的情况,并且确保child指向的是较大的叶子结点
while(child < len){
//这里判断两次 child < len 是为了防止后续++导致越界
if(child < len && elem[child] < elem[child + 1]){
child++;
}
//这里找到最大的孩子后,就需要进行交换操作
if(elem[parent] < elem[child]){
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
//这里交换之后进不能保证树后面是否还存在元素
parent = child;
child = child*2 + 1;
}else{
//不进行上述操作表明符合条件
break;
}
}
}
简单图解向下调整:
这里,我们就不用上面的10个数字,简单设定几个数字进行解释。如图:
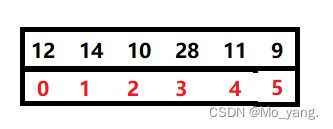
我们已经知道,在优先级队列中,未排序的数组在逻辑上是二叉树的形式,并且以先序遍历的形式存在即(根 -> 左 -> 右),所以对上图进行罗列得到下图:
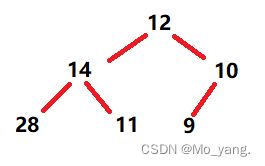
在上面我们说过:如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2。

对于这句代码,我们需要明确,当前我们所做的是向下调整,因此,这样我们可以最先获取到二叉树最底层叶子结点的父节点这样可以更容易的将较大值向上移动而不遗留,随着 parent- - 就不会遗漏任何一个节点。
通过上面的循环,第一次进入到 shiftdown 方法,如图:
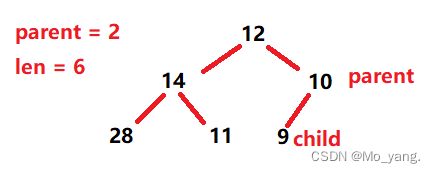

首先遇到这行代码,很显然在往后已经没有数字了一开始就不符合划红线的情况
![]()
下面这行交换代码也不符合情况,这就说明此处的顺序是正确的,也就直接跳出,parent-- 后进行下次循环。
再次进入 shiftdown 方法此时情况如下:
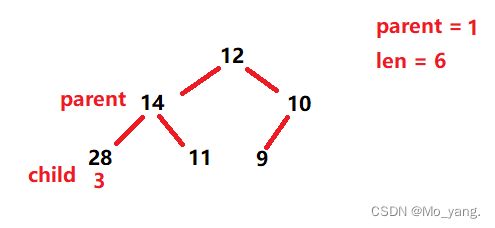
此时进入while后在第一个 if 语句中判断不符合条件,直接进入第二个 if 语句
![]()
此时发现满足上述语句,进入后进行交换。之后再次进入到下一次循环。
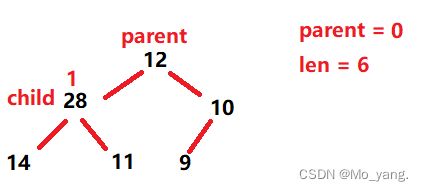
如上图所示,parent 此时已经指向 0 下标元素,表明已经是最后一次判断是否交换。很显然是要交换的,最终,如下图所示:
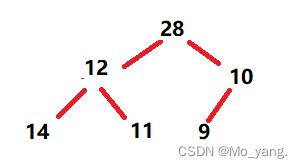
下面是代码整体运行
如图:
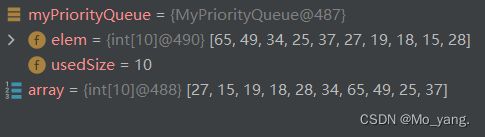
到这里就说明大根堆的创建完毕。
实现插入操作:
插入操作要考虑的问题有以下几点:
1.再添加元素时,需要注意数组是否已满
2.添加的元素位置是要添加在数组的末尾,即就是树的最后一个结点。
3.添加的元素要进行上移操作
//首先实现一个插入元素的方法
public void offer(int val){
//首先要判断数组是否已满
if(isFull()){
//如果数组已满则需要扩容操作
elem = Arrays.copyOf(this.elem,2*this.elem.length);
}
this.elem[usedSize] = val;
//插入后就需要对元素进行合理的位置改变
}
//实现一个向上转移的方法
private void shiftUp(int child){
//首先要找到插入节点的父亲节点
int parent = (child - 1)/2;
while(child > 0){
if(elem[child] > elem[parent]){
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
child = parent;
parent = (child - 1)/2;
}else{
break;
}
}
}
//实现一个判满方法
public boolean isFull(){
return usedSize == elem.length;
}
实现删除操作
删除操作需要注意,思考的问题:
删除,是要删除堆顶的元素,这里就要将第一个元素和最后一个元素进行交换,在进行向下调整。
//这里要注意栈是否为空的情况
public void pop(){
if(isEmpty()){
return -1;
}
//实现要删除的元素和最后一个元素交换
int tmp = elem[0];
elem[0] = elem[usedSize - 1];
elem[usedSize - 1] = tmp;
usedSize--;
//上下元素进行调整后,顶部的元素会变小,所以需要向下调整
shiftDown(0,usedSize);
return tmp;
}
public boolean isEmpty(){
return usedSize == 0;
}

