杨氏矩阵 图解模拟实现 + 杨辉三角

1、杨氏矩阵

一、题目概述

有一个数字矩阵，矩阵的每行从左到右是递增的，矩阵从上到下是递增的，请编写程序在这样的矩阵中查找某个数字是否存在。

二、解题思路

什么是杨氏矩阵？

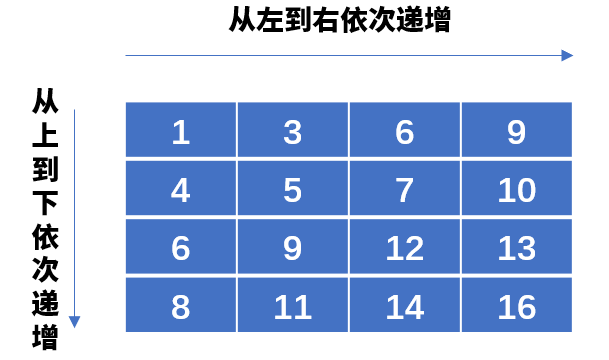
如上图：杨氏矩阵行从左到右都是递增的，从上到下都是递增的，这个就是杨氏矩阵。
那么我们应该如何实现在矩阵里面找出某个数字到底存不存在呢？

方法：“右上角”法

先定义行i ，列j
从右上角的数字开始，跟要找的数字进行比较，比如说我要找的是8，如果矩阵中的元素大于8，那么j–
如果矩阵中的元素小于8，那么i++

为什么用这个方法？

如上图：很明显，杨氏矩阵可以看作是一个二维数组，二维数组存放着四个一维数组
因为杨氏矩阵他是从左到右从上到下递增，如果我从右上角开始寻找，那么他是第一行一维数组里面的最大的数字，比如说9，比我要找的8大，那么按照从上到下递增的特性，你8比我9还小，那么8就不可能是9处于的那一列，j–，这里具体后面会模拟实现
同理，j–后得到的6跟8比较，6<8，由于从左到右递增的特性，6都已经小于8了，那么6左边的元素都小于8，所以i++，依此类推

三、代码实现

#define _CRT_SECURE_NO_WARNINGS 1
#include 
int FindNum(int arr[4][4], int k, int* pi, int* pj)
{
	//数组下标
	int i = 0;
	int j = *pj - 1;
	//开始寻找数字
	while (i < *pj && j >= 0) //判断坐标合法性
	{
		if (arr[i][j] < k)
		{
			i++;
		}
		else if (arr[i][j] > k)
		{
			j--;
		}
		else
		{
			*pi = i;	//把找到的数组下标赋给指针变量，这样出了函数也不会被销毁，这就是传址调用
			*pj = j;
			return 1;	//找到了返回1
		}
	}
	return 0;
}
int main()
{
	int k = 0;
	int arr[4][4] = { {1,3,6,9}, {4,5,7,10},{6,9,12,13}, {8,11,14,16} };

	scanf("%d", &k);
	int i = 4;
	int j = 4;

	int ret = FindNum(arr, k, &i, &j);

	if (ret == 1)
	{
		printf("找到了，数组下标为：%d %d\n", i, j);
	}
	else
	{
		printf("找不到\n");
	}


	return 0;
}

四、模拟实现

下面开始模拟实现，这个是数组下标初始完后的样子

我们从右上角开始比较，也就是i = 0; j = *pj - 1的时候，也就是arr[0][3] = 9与8比较,发现9比8大，根据从上到下递增的特性，9是第三列最小的数，8连第三列最小的数9都打不过，更何况是后面的数字，所以8不可能是第三列的数字，j–，如下图：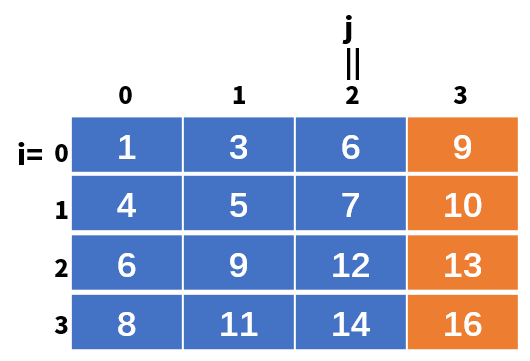

然后判断坐标合法性，i < 4 && j >= 0 符合条件，进入循环
此时arr[i][j]继续比较，也就是arr[0][2]，6和8进行比较，发现6比8小，6是第一行最大的数（第三列已经在上面排除，所以最大的数字6），最大的数字6都没8大，那么根据从左到右递增的特性，那么6及其6左边的数字都不会比8大，此时i++，如下图：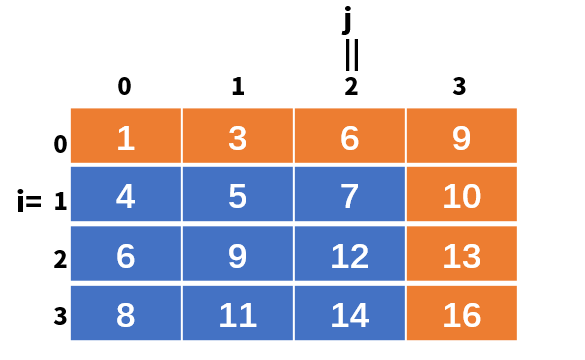

然后继续循环，判断坐标合法性，i < 4 && j >= 0 符合条件，进入循环
此时arr[i][j]继续比较，也就是arr[1][2]，7和8进行比较，发现7比8小，7是第二行最大的数（第三列已经在上面排除，所以最大的数字7），最大的数字7都没8大，那么根据从左到右递增的特性，那么7及其7左边的数字都不会比8大，此时i++，如下图：

然后继续循环，判断坐标合法性，i < 4 && j >= 0 符合条件，进入循环
此时arr[i][j]继续比较，也就是arr[2][2]，12和8进行比较，发现12比8大，12是第二列未排除的数中最小的数，8连12的打不过，根据从上到下递增的特性，那么第二列未排除的数字12都打不过，12以及下面的数字肯定也打不过，所以j–，如下图：

然后继续循环，判断坐标合法性，i < 4 && j >= 0 符合条件，进入循环
此时arr[i][j]继续比较，也就是arr[2][2]，9和8进行比较，发现9比8大，9是第一列未排除的数中最小的数，8连9的打不过，根据从上到下递增的特性，那么第一列未排除的数字9都打不过，9以及下面的数字肯定也打不过，所以j–，如下图：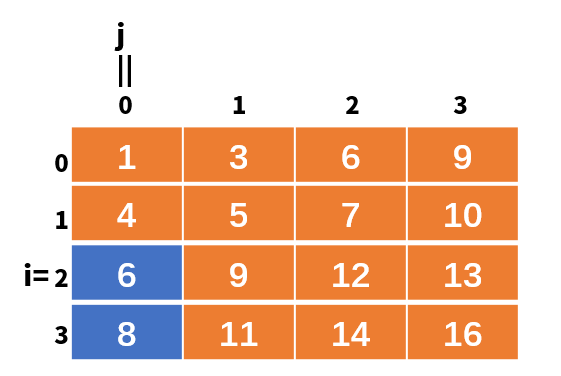

然后继续循环，判断坐标合法性，i < 4 && j >= 0 符合条件，进入循环
此时arr[i][j]继续比较，也就是arr[2][0]，6和8进行比较，发现6比8小，6是第三行未排除的数字中最大的数，最大的数字6都没8大，那么根据从左到右递增的特性，那么6及其6左边的数字都不会比8大，（不过此时已经没左边数字了），此时i++，如下图：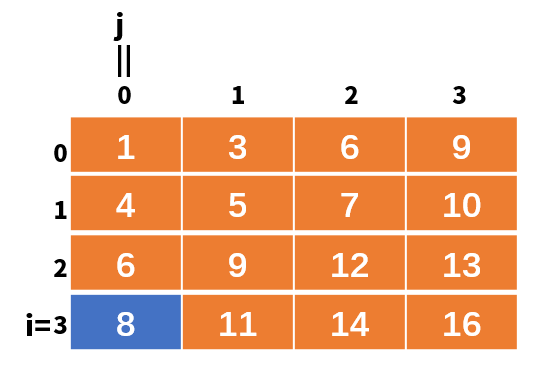

然后继续循环，判断坐标合法性，i < 4 && j >= 0 符合条件，进入循环
此时arr[i][j]继续比较，也就是arr[3][0]，8和8进行比较，相等，把i和j的下标赋给指针变量，然后返回1

模拟实现结束。

2、杨辉三角

一、题目概述

在屏幕上打印杨辉三角。

1

1 1

1 2 1

1 3 3 1

……

二、解题思路

什么是杨辉三角?

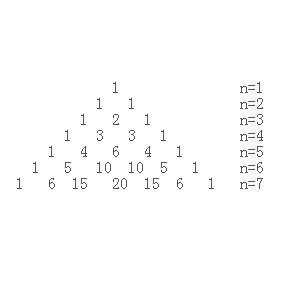
简单总结四点：

1. 每个数等于它上方两数之和。
2. 每行数字左右对称，由1开始逐渐变大。
3. 第n行的数字有n项。
4. 第n行第一个数字和最后一个数字都是1

如何实现？

呜呜j = 0

i= 0 1

i = 1 1 1

i = 2 1 2 1

i = 3 1 3 3 1

如上所示，

• 整个数组打印
  • 如果要打印这样的数组，只需要列等于行即可
• 开头和最后打印
  • 无论是第几行，第一个数字和最后一个数字都是1，那么代表j=0时，一定是1，然后i和j相等的时候一定是1
• 中间的数字打印
  • 每个数都等于它上方两数之和，即arr[i - 1][j] +arr[i - 1][j -1]

三、代码实现

#define _CRT_SECURE_NO_WARNINGS 1
#include 
void YanghuiTriangle(int arr[4][4], int n)
{
	int i = 0;
	int j = 0;
	for (i = 0; i < n; i++)
	{
		for (j = 0; j <= i; j++)
		{
			if (j == 0)
			{
				arr[i][j] = 1;
			}
			else if (j == i)
			{
				arr[i][j] = 1;
			}
			else
			{
				arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
			}

		}
	}
}
int main()
{
	int arr[4][4] = { 0 };
	int n = 4;
	YanghuiTriangle(arr, 4);

	int i = 0;
	int j = 0;
	for (i = 0; i < n; i++)
	{
		for (j = 0; j <= i; j++)
		{
			printf("%d ", arr[i][j]);
		}
		printf("\n");
	}

	return 0;
}