对称加密、非对称加密、DES、AES、RSA、OpenSSL、数字签名、防篡改
本公众号分享的所有技术仅用于学习交流,请勿用于其他非法活动,如果错漏,欢迎留言指正
《加密与解密》第4版
加解密
- 安全领域的重要分支和基础设施
互联网重要数据的传输需要加解密- TCP/IP协议本身是明文的,不安全
- 比如登陆时候用户名和密码
- 比如收发的电子邮件。
- QQ聊天内容(对公安机关开放解密接口,可以看到聊天记录),曾经恐怖分子还列出一份
安全IM工具列表 - 加密议包括:https/tls/ssl等
- http是明文的(所以有可能是
钓鱼网站),https是加密的,即使被嗅探到,解密可能需要耗费的时间是10W年级别,几乎不可能。
- http是明文的(所以有可能是
重要数据存储也需要加密:- NTFS的EFS(合法用户登陆进入系统才能看到硬盘的内容,如果硬盘被拆下来装在其他的电脑上看到的是加密后的密文,破解需要耗费时间是10W年的级别,
对称加密和非对称加密结合起来的方式,是现在最安全的一种加密方式) - WINRAR的文件加密等
- res加密算法,美国推荐的标准加密算法
- 密钥随机,包含数字,字母,符号
- 备份自己的密码(显示密码中的几位作为提示),避免自己忘了,自己都解不开
- NTFS的EFS(合法用户登陆进入系统才能看到硬盘的内容,如果硬盘被拆下来装在其他的电脑上看到的是加密后的密文,破解需要耗费时间是10W年的级别,
防止文件被篡改,也需要数字签名- dll文件等
- 公安犯罪记录保存,防止被篡改
一、加解密算法的分类
1. 对称加密
- 单钥密码系统的加密方法,同一个密钥可以同时用作信息的加密和解密,这种加密方法称为
对称加密,也称为单密钥加密。- 密钥是控制加密及解密过程的指令,在对称加密中,数据发送方用加密密钥和特殊加密算法对明文(原始数据)加密,使其变成复杂的加密密文发送出去。接收方收到密文后,若想解读原文,则需要使用加密密钥及相同算法的
逆算法对密文进行解密,才能使其恢复成可读明文。 - 在对称加密算法中,使用的密钥只有一个,发收信双方都使用这个密钥对数据进行加密和解密。
- 优点:算法公开、计算量小、加密速度快、加密效率高
- 缺点:密钥管理
- 密钥是控制加密及解密过程的指令,在对称加密中,数据发送方用加密密钥和特殊加密算法对明文(原始数据)加密,使其变成复杂的加密密文发送出去。接收方收到密文后,若想解读原文,则需要使用加密密钥及相同算法的
2. 非对称加密
- 非对称加密算法需要两个密钥来进行加密和解密,这两个密钥是公开密钥( public key,简称
公钥)和私有密钥(private key,简称私钥) - 如果用公钥对数据进行加密,只有对应的私钥才能解密。如果用私钥对数据进行加密,那么只有对应的公钥才能解密。因为加密和解密使用的是两个不同的密钥,所以这种算法叫做
非对称加密算法。 - eg: A,B用非对称加密通信:
- 1)A生成一对密钥(公钥和私钥)并将公钥向其它方公开,私钥独自严格保密。
- 2)得到该公钥的B使用该密钥对机密信息进行加密后再发送给A方。
- 3)A方再用自己保存的另一把专用密钥(私钥)对加密后的信息进行解密。A方只能用其专用密钥(私钥)解密由对应的公钥加密后的信息。
- 在传输过程中,即使攻击者截获了传输密文,并得到A的公钥,也无法破解密文,因为只有A的私钥才能解密密文。
- 同样,如果A回复加密信息给B,那么需要B先公布B的公钥给A用于加密,B自己保存B的私钥用于解密。
- 优点:密钥管理的安全性更好(不需要像对称加密那样,要把密钥告诉很多人,只需要把公钥告诉其他人)
- 缺点:加密和解密花费时间长、速度慢,只适合对少量数据进行加密。所以一般是是对称加密与非对称加密相结合。
- 加密:用对称加密来加密数据得到密文A,用非对称加密加密对称加密的密钥得到密文B,把AB放到一起
- 解密:先用非对称解密密文B得到对称加密的密钥,用这个密钥再去解密密文A得到原来的数据
3. 散列算法
- 散列(Hash)函数对不同长度的输入消息,产生固定长度(比如MD5是16字节(128位)的输出
- 这个固定长度的输出称为原输入消想的“
散列"或“消息摘要”(Message digest)。
- 这个固定长度的输出称为原输入消想的“
- 一个安全的哈希函数H必须具有以下属性:
- 1)能够应用到
大小不一的数据上。 - 2)H能够生成
大小固定的输出 - 3)对于任意给定的x,H(×)的计算
相对简单。 - 4)对于任意给定的代码h,要发现满足H(x)=h的x在计算上是不可行的。(通过hash值无法反推出原数据,但可以破解,比如可以通过设定一个字典,计算出每一个单词的hash值,通过一一碰撞,就得到加密前的原文)
- 5)对于任意给定的块x,要发现满足H=H(x)而y=×在计算上是不可行的。(两个hash值相同,但不能推断出原来两个值也相同)
- 1)能够应用到
- 应用:错误矫正,文件校验(奇偶校验,CRC,无防篡改功能),数字签名等
4. 侧重点
- 对称加密:
XORDES、3DESAES Advanced Encryption Standard(工业标准)- Blowfish
- twofish
- 非对称加密:
RSA(两个大的素数(几十个字节的长度)之积,很难进行因式分解还原回原来的两个素数)- Elgamal
- 背包算法
- Rabin
- D-H
- ECC(圆曲线加密算法)
- 散列HASH算法:
- MD5 Message-Digest Algorithm5
- SHA1 SHA2 (SHA-256,512)Secure Hash Algorithm.
- 重点在加密解密的
接口调用和应用,而不是加密解密算法本身的实现(数论,矩阵等)
二、加解密算法详解
1. 对称加密:异或算法
- A为明文,B为密文
- 加密:B=A^key
- 解密:A=B^key
- 丑闻:360密盘号称10W年无法破解,但一下子就被破解了,当时360把密盘项目外包出去了,外包人员图方便使用了异或算法,而且把密钥放在密文前面,最离谱的是把代码提交给360审计的时候还通过了。

#include 2. 对称加密:DES算法
- DES全称为Data Encryption Standard,即数据加密标准,是一种使用密钥加密的
块算法。- DES是可以被破解的,可能一本书的某一句话就是密钥。
- DES算法的入口参数有三个:Key、Data、Mode。其中Key为7个字节共64位,是DES算法的工作密钥; Data为8个字节64位(加密以8Byte为基本单位),是要被加密或被解密的数据;Mode为DES的工作方式,有两种:加密或解密
- 比如加密数据有20Byte,以8Byte为基本单位,后面4个Byte不足8个Byte,填4Byte的0组成8个Byte进行加密。
- 3DES (即Triple DES是DES向AES过渡的加密算法,它使用
3条56位的密钥对数据进行三次加密。是DES的个更安全的变形。它以DES为基本模块,通过组合分组方法设计出分组加密算法。比起最初的DES,3DES更为安全。 - 纯C写的和OpenSSL都是可移植的,比微软的CryptoAPI好(只能在windows下使用),des.c和des.h是des加解密算法的实现
// des_test.c
//
#include "stdio.h"
#include "stdlib.h"
#include "des.h"
#include /// des.h
#include "stdio.h"
#include "memory.h"
#include "stdlib.h"
#define PLAIN_FILE_OPEN_ERROR -1
#define KEY_FILE_OPEN_ERROR -2
#define CIPHER_FILE_OPEN_ERROR -3
#define DES_OK 1
#define BUFFER_SIZE 1024
#define ROUND 16//迭代次数,16次以上破解时只能使用穷举法
typedef char ElemType;
int ByteToBit(ElemType ch,ElemType bit[8]);//字节转换成二进制
int BitToByte(ElemType bit[8],ElemType *ch);//二进制转换成字节
int Char8ToBit64(ElemType ch[8],ElemType bit[64]);//将长度为8的字符串转为二进制位串
int Bit64ToChar8(ElemType bit[64],ElemType ch[8]);//将二进制位串转为长度为8的字符串
int DES_MakeSubKeys(ElemType key[64],ElemType subKeys[16][48]);//生成子密钥
int DES_PC1_Transform(ElemType key[64], ElemType tempbts[56]);//密钥置换1
int DES_PC2_Transform(ElemType key[56], ElemType tempbts[48]);//密钥置换2
int DES_ROL(ElemType data[56], int time);//循环左移
int DES_IP_Transform(ElemType data[64]);//IP置换
int DES_IP_1_Transform(ElemType data[64]);//IP逆置换
int DES_E_Transform(ElemType data[48]);//扩展置换
int DES_P_Transform(ElemType data[32]);//P置换
int DES_SBOX(ElemType data[48]);//S盒置换
int DES_XOR(ElemType R[48], ElemType L[48],int count);//异或
int DES_Swap(ElemType left[32],ElemType right[32]);//交换
int DES_EncryptBlock(ElemType plainBlock[8], ElemType subKeys[16][48], ElemType cipherBlock[8]);//加密单个分组
int DES_DecryptBlock(ElemType cipherBlock[8], ElemType subKeys[16][48], ElemType plainBlock[8]);//解密单个分组
//DES算法
int DES_Encrypt(ElemType *plainBuffer, ElemType *keyBuffer, ElemType *cipherBuffer, int n);//加密数据
int DES_Decrypt(ElemType *cipherBuffer, ElemType *keyBuffer, ElemType *plainBuffer, int n);//解密数据
int DES_Encrypt_File(char *plainFile, char *keyStr,char *cipherFile);//加密文件
int DES_Decrypt_File(char *cipherFile, char *keyStr,char *plainFile);//解密文件
//3DES算法
int D3DES_Encrypt(ElemType *plainBuffer, ElemType *keyBuffer, ElemType *cipherBuffer, int n);//加密数据
int D3DES_Decrypt(ElemType *cipherBuffer, ElemType *keyBuffer, ElemType *plainBuffer, int n);//解密数据
int D3DES_Encrypt_File(char *plainFile, char *keyStr,char *cipherFile);//加密文件
int D3DES_Decrypt_File(char *cipherFile, char *keyStr,char *plainFile);//解密文件
//初始置换表IP
static int IP_Table[64] = { 57,49,41,33,25,17,9,1,
59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,
63,55,47,39,31,23,15,7,
56,48,40,32,24,16,8,0,
58,50,42,34,26,18,10,2,
60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6};
//逆初始置换表IP^-1
static int IP_1_Table[64] = {39,7,47,15,55,23,63,31,
38,6,46,14,54,22,62,30,
37,5,45,13,53,21,61,29,
36,4,44,12,52,20,60,28,
35,3,43,11,51,19,59,27,
34,2,42,10,50,18,58,26,
33,1,41,9,49,17,57,25,
32,0,40,8,48,16,56,24};
//扩充置换表E
static int E_Table[48] = {31, 0, 1, 2, 3, 4,
3, 4, 5, 6, 7, 8,
7, 8,9,10,11,12,
11,12,13,14,15,16,
15,16,17,18,19,20,
19,20,21,22,23,24,
23,24,25,26,27,28,
27,28,29,30,31, 0};
//置换函数P
static int P_Table[32] = {15,6,19,20,28,11,27,16,
0,14,22,25,4,17,30,9,
1,7,23,13,31,26,2,8,
18,12,29,5,21,10,3,24};
//S盒
static int S[8][4][16] =//S1
{{{14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7},
{0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8},
{4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0},
{15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13}},
//S2
{{15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10},
{3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5},
{0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15},
{13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9}},
//S3
{{10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8},
{13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1},
{13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7},
{1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12}},
//S4
{{7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15},
{13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9},
{10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4},
{3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14}},
//S5
{{2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9},
{14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6},
{4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14},
{11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3}},
//S6
{{12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11},
{10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8},
{9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6},
{4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13}},
//S7
{{4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1},
{13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6},
{1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2},
{6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12}},
//S8
{{13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7},
{1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2},
{7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8},
{2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11}}};
//置换选择1
static int PC_1[56] = {56,48,40,32,24,16,8,
0,57,49,41,33,25,17,
9,1,58,50,42,34,26,
18,10,2,59,51,43,35,
62,54,46,38,30,22,14,
6,61,53,45,37,29,21,
13,5,60,52,44,36,28,
20,12,4,27,19,11,3};
//置换选择2
static int PC_2[48] = {13,16,10,23,0,4,2,27,
14,5,20,9,22,18,11,3,
25,7,15,6,26,19,12,1,
40,51,30,36,46,54,29,39,
50,44,32,46,43,48,38,55,
33,52,45,41,49,35,28,31};
//左移次数规定
static int MOVE_TIMES[16] = {1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1};
/// des.c
#include "des.h"
#pragma warning(disable:4996)
//字节转换成二进制
int ByteToBit(ElemType ch, ElemType bit[8]){
int cnt;
for(cnt = 0;cnt < 8; cnt++){
*(bit+cnt) = (ch>>cnt)&1;
}
return 0;
}
//二进制转换成字节
int BitToByte(ElemType bit[8],ElemType *ch){
int cnt;
for(cnt = 0;cnt < 8; cnt++){
*ch |= *(bit + cnt)<<cnt;
}
return 0;
}
//将长度为8的字符串转为二进制位串
int Char8ToBit64(ElemType ch[8],ElemType bit[64]){
int cnt;
for(cnt = 0; cnt < 8; cnt++){
ByteToBit(*(ch+cnt),bit+(cnt<<3));
}
return 0;
}
//将二进制位串转为长度为8的字符串
int Bit64ToChar8(ElemType bit[64],ElemType ch[8]){
int cnt;
memset(ch,0,8);
for(cnt = 0; cnt < 8; cnt++){
BitToByte(bit+(cnt<<3),ch+cnt);
}
return 0;
}
//生成子密钥
int DES_MakeSubKeys(ElemType key[64],ElemType subKeys[16][48]){
ElemType temp[56];
int cnt;
DES_PC1_Transform(key,temp);//PC1置换
for(cnt = 0; cnt < ROUND; cnt++){//16轮跌代,产生16个子密钥
DES_ROL(temp,MOVE_TIMES[cnt]);//循环左移
DES_PC2_Transform(temp,subKeys[cnt]);//PC2置换,产生子密钥
}
return 0;
}
//密钥置换1
int DES_PC1_Transform(ElemType key[64], ElemType tempbts[56]){
int cnt;
for(cnt = 0; cnt < 56; cnt++){
tempbts[cnt] = key[PC_1[cnt]];
}
return 0;
}
//密钥置换2
int DES_PC2_Transform(ElemType key[56], ElemType tempbts[48]){
int cnt;
for(cnt = 0; cnt < 48; cnt++){
tempbts[cnt] = key[PC_2[cnt]];
}
return 0;
}
//循环左移
int DES_ROL(ElemType data[56], int time){
ElemType temp[56];
//保存将要循环移动到右边的位
memcpy(temp,data,time);
memcpy(temp+time,data+28,time);
//前28位移动
memcpy(data,data+time,28-time);
memcpy(data+28-time,temp,time);
//后28位移动
memcpy(data+28,data+28+time,28-time);
memcpy(data+56-time,temp+time,time);
return 0;
}
//IP置换
int DES_IP_Transform(ElemType data[64]){
int cnt;
ElemType temp[64];
for(cnt = 0; cnt < 64; cnt++){
temp[cnt] = data[IP_Table[cnt]];
}
memcpy(data,temp,64);
return 0;
}
//IP逆置换
int DES_IP_1_Transform(ElemType data[64]){
int cnt;
ElemType temp[64];
for(cnt = 0; cnt < 64; cnt++){
temp[cnt] = data[IP_1_Table[cnt]];
}
memcpy(data,temp,64);
return 0;
}
//扩展置换
int DES_E_Transform(ElemType data[48]){
int cnt;
ElemType temp[48];
for(cnt = 0; cnt < 48; cnt++){
temp[cnt] = data[E_Table[cnt]];
}
memcpy(data,temp,48);
return 0;
}
//P置换
int DES_P_Transform(ElemType data[32]){
int cnt;
ElemType temp[32];
for(cnt = 0; cnt < 32; cnt++){
temp[cnt] = data[P_Table[cnt]];
}
memcpy(data,temp,32);
return 0;
}
//异或
int DES_XOR(ElemType R[48], ElemType L[48] ,int count){
int cnt;
for(cnt = 0; cnt < count; cnt++){
R[cnt] ^= L[cnt];
}
return 0;
}
//S盒置换
int DES_SBOX(ElemType data[48]){
int cnt;
int line,row,output;
int cur1,cur2;
for(cnt = 0; cnt < 8; cnt++){
cur1 = cnt*6;
cur2 = cnt<<2;
//计算在S盒中的行与列
line = (data[cur1]<<1) + data[cur1+5];
row = (data[cur1+1]<<3) + (data[cur1+2]<<2)
+ (data[cur1+3]<<1) + data[cur1+4];
output = S[cnt][line][row];
//化为2进制
data[cur2] = (output&0X08)>>3;
data[cur2+1] = (output&0X04)>>2;
data[cur2+2] = (output&0X02)>>1;
data[cur2+3] = output&0x01;
}
return 0;
}
//交换
int DES_Swap(ElemType left[32], ElemType right[32]){
ElemType temp[32];
memcpy(temp,left,32);
memcpy(left,right,32);
memcpy(right,temp,32);
return 0;
}
//加密单个分组
int DES_EncryptBlock(ElemType plainBlock[8], ElemType subKeys[16][48], ElemType cipherBlock[8]){
ElemType plainBits[64];
ElemType copyRight[48];
int cnt;
Char8ToBit64(plainBlock,plainBits);
//初始置换(IP置换)
DES_IP_Transform(plainBits);
//16轮迭代
for(cnt = 0; cnt < ROUND; cnt++){
memcpy(copyRight,plainBits+32,32);
//将右半部分进行扩展置换,从32位扩展到48位
DES_E_Transform(copyRight);
//将右半部分与子密钥进行异或操作
DES_XOR(copyRight,subKeys[cnt],48);
//异或结果进入S盒,输出32位结果
DES_SBOX(copyRight);
//P置换
DES_P_Transform(copyRight);
//将明文左半部分与右半部分进行异或
DES_XOR(plainBits,copyRight,32);
if(cnt != ROUND - 1){
//最终完成左右部的交换
DES_Swap(plainBits,plainBits+32);
}
}
//逆初始置换(IP^1置换)
DES_IP_1_Transform(plainBits);
Bit64ToChar8(plainBits,cipherBlock);
return 0;
}
//解密单个分组
int DES_DecryptBlock(ElemType cipherBlock[8], ElemType subKeys[16][48],ElemType plainBlock[8]){
ElemType cipherBits[64];
ElemType copyRight[48];
int cnt;
Char8ToBit64(cipherBlock,cipherBits);
//初始置换(IP置换)
DES_IP_Transform(cipherBits);
//16轮迭代
for(cnt = ROUND - 1; cnt >= 0; cnt--){
memcpy(copyRight,cipherBits+32,32);
//将右半部分进行扩展置换,从32位扩展到48位
DES_E_Transform(copyRight);
//将右半部分与子密钥进行异或操作
DES_XOR(copyRight,subKeys[cnt],48);
//异或结果进入S盒,输出32位结果
DES_SBOX(copyRight);
//P置换
DES_P_Transform(copyRight);
//将明文左半部分与右半部分进行异或
DES_XOR(cipherBits,copyRight,32);
if(cnt != 0){
//最终完成左右部的交换
DES_Swap(cipherBits,cipherBits+32);
}
}
//逆初始置换(IP^1置换)
DES_IP_1_Transform(cipherBits);
Bit64ToChar8(cipherBits,plainBlock);
return 0;
}
/*加密数据(字符串)
*plainBuffer:输入数据
*keyBuffer:密钥(8字节)
*cipherBuffer:输出数据
*n:加密数据长度
*/
int DES_Encrypt(ElemType *plainBuffer, ElemType *keyBuffer, ElemType *cipherBuffer, int n){
int des_size = n;
int des_count = 0;
int count = 0;
ElemType plainBlock[8],cipherBlock[8],keyBlock[8];
ElemType bKey[64];
ElemType subKeys[16][48];
//设置密钥
memcpy(keyBlock,keyBuffer,8);
//将密钥转换为二进制流
Char8ToBit64(keyBlock,bKey);
//生成子密钥
DES_MakeSubKeys(bKey,subKeys);
while (des_count + 8 <= des_size){
memcpy(plainBlock,plainBuffer + des_count,8);
DES_EncryptBlock(plainBlock,subKeys,cipherBlock);
memcpy(cipherBuffer + des_count,cipherBlock,8) ;
des_count += 8;
}
if((count = des_size - des_count)){
memcpy(plainBlock,plainBuffer + des_count,count);
//填充
memset(plainBlock + count,'\0',7 - count);
//最后一个字符保存包括最后一个字符在内的所填充的字符数量
plainBlock[7] = 8 - count;
DES_EncryptBlock(plainBlock,subKeys,cipherBlock);
memcpy(cipherBuffer + des_count,cipherBlock,8);
}
return DES_OK;
}
/*解密数据(字符串)
*cipherBuffer:输入数据
*keyBuffer:密钥(8字节)
*plainBuffer:输出数据
*n:解密数据长度
*返回解密后数据长度
*/
int DES_Decrypt(ElemType *cipherBuffer, ElemType *keyBuffer, ElemType *plainBuffer, int n){
int des_size = n;
int des_count = 0;
int count = 0;
ElemType plainBlock[8],cipherBlock[8],keyBlock[8];
ElemType bKey[64];
ElemType subKeys[16][48];
//设置密钥
memcpy(keyBlock,keyBuffer,8);
//将密钥转换为二进制流
Char8ToBit64(keyBlock,bKey);
//生成子密钥
DES_MakeSubKeys(bKey,subKeys);
while(1){
memcpy(cipherBlock,cipherBuffer + des_count,8);
DES_DecryptBlock(cipherBlock,subKeys,plainBlock);
if(des_count + 8 < des_size){
memcpy(plainBuffer + des_count,plainBlock,8);
des_count += 8;
} else {
break;
}
}
//判断末尾是否被填充
if(plainBlock[7] < 8){
for(count = 8 - plainBlock[7]; count < 7; count++){
if(plainBlock[count] != '\0'){
break;
}
}
}
if(count == 7){
memcpy(plainBuffer + des_count,plainBlock,8 - plainBlock[7]);
return des_count +8 - plainBlock[7];
} else {
memcpy(plainBuffer + des_count,plainBlock,8);
return des_count +8 ;
}
return des_count + 8;
}
//加密文件
int DES_Encrypt_File(char *plainFile, char *keyStr,char *cipherFile){
FILE *plain,*cipher,*key;
ElemType *plainBlock,*cipherBlock,keyBlock[8];
long fileLen_in,fileLen_out;
int count;
if((plain = fopen(plainFile,"rb")) == NULL){
return PLAIN_FILE_OPEN_ERROR;
}
if((key = fopen(keyStr,"rb")) == NULL){
return KEY_FILE_OPEN_ERROR;
}
if((cipher = fopen(cipherFile,"wb")) == NULL){
return CIPHER_FILE_OPEN_ERROR;
}
if((count = fread(keyBlock,sizeof(char),8,key)) == 8){
}
fseek(plain,0,SEEK_END);//将文件指针置尾
fileLen_out = fileLen_in = ftell(plain);//取文件指针当前位置
rewind(plain);//将文件指针重指向文件头
if (fileLen_in % 8 != 0)
fileLen_out = (fileLen_in/8+1)*8;
plainBlock = (ElemType *)malloc(fileLen_out * sizeof(ElemType));
cipherBlock = (ElemType *)malloc(fileLen_out * sizeof(ElemType));
fread(plainBlock,sizeof(char),fileLen_in,plain);
DES_Encrypt(plainBlock,keyBlock,cipherBlock,fileLen_in);
fwrite(cipherBlock,sizeof(char),fileLen_out,cipher);
fclose(plain);
fclose(cipher);
fclose(key);
free(plainBlock);
free(cipherBlock);
return DES_OK;
}
//解密文件
int DES_Decrypt_File(char *cipherFile, char *keyStr,char *plainFile){
FILE *plain,*cipher,*key;
ElemType *plainBlock,*cipherBlock,keyBlock[8];
int count;
long fileLen_in,fileLen_out;
if((plain = fopen(plainFile,"wb")) == NULL){
return PLAIN_FILE_OPEN_ERROR;
}
if((key = fopen(keyStr,"rb")) == NULL){
return KEY_FILE_OPEN_ERROR;
}
if((cipher = fopen(cipherFile,"rb")) == NULL){
return CIPHER_FILE_OPEN_ERROR;
}
if((count = fread(keyBlock,sizeof(char),8,key)) == 8){
}
fseek(cipher,0,SEEK_END);//将文件指针置尾
fileLen_out = fileLen_in = ftell(cipher);//取文件指针当前位置
rewind(cipher);//将文件指针重指向文件头
plainBlock = (ElemType *)malloc(fileLen_in * sizeof(ElemType));
cipherBlock = (ElemType *)malloc(fileLen_in * sizeof(ElemType));
fread(cipherBlock,sizeof(char),fileLen_in,cipher);
count = DES_Decrypt(cipherBlock,keyBlock,plainBlock,fileLen_in);
fwrite(plainBlock,sizeof(char),count,plain);
fclose(plain);
fclose(cipher);
fclose(key);
free(plainBlock);
free(cipherBlock);
return DES_OK;
}
/*3DES加密数据(字符串)
*对区块使用3个64位密钥进行3次加密,相当于增加了密钥长度
*plainBuffer:输入数据
*keyBuffer:密钥(24字节)
*cipherBuffer:输出数据
*n:加密数据长度
*/
int D3DES_Encrypt(ElemType *plainBuffer, ElemType *keyBuffer, ElemType *cipherBuffer, int n){
int des_size = n;
int des_count = 0;
int count = 0;
int i;
ElemType plainBlock[8],cipherBlock[8],keyBlock[24];
ElemType bKey[3][64];
ElemType subKeys[3][16][48];
for (i = 0; i < 3 ; i++)
{
//设置密钥
memcpy(keyBlock+i*8,keyBuffer+i*8,8);
//将密钥转换为二进制流
Char8ToBit64(keyBlock+i*8,bKey[i]);
//生成子密钥
DES_MakeSubKeys(bKey[i],subKeys[i]);
}
while (des_count + 8 <= des_size){
memcpy(plainBlock,plainBuffer + des_count,8);
for (i = 0; i < 3 ; i++)
{
DES_EncryptBlock(plainBlock,subKeys[i],cipherBlock);
}
memcpy(cipherBuffer + des_count,cipherBlock,8) ;
des_count += 8;
}
if((count = des_size - des_count)){
memcpy(plainBlock,plainBuffer + des_count,count);
//填充
memset(plainBlock + count,'\0',7 - count);
//最后一个字符保存包括最后一个字符在内的所填充的字符数量
plainBlock[7] = 8 - count;
{
for (i = 0; i < 3 ; i++)
{
DES_EncryptBlock(plainBlock,subKeys[i],cipherBlock);
}
}
memcpy(cipherBuffer + des_count,cipherBlock,8);
}
return DES_OK;
}
/*3DES解密数据(字符串)
*cipherBuffer:输入数据
*keyBuffer:密钥(24字节)
*plainBuffer:输出数据
*n:解密数据长度
*返回解密后数据长度
*/
int D3DES_Decrypt(ElemType *cipherBuffer, ElemType *keyBuffer, ElemType *plainBuffer, int n){
int des_size = n;
int des_count = 0;
int count = 0;
int i;
ElemType plainBlock[8],cipherBlock[8],keyBlock[24];
ElemType bKey[3][64];
ElemType subKeys[3][16][48];
for (i = 0; i < 3 ; i++)
{
//设置密钥
memcpy(keyBlock+i*8,keyBuffer+i*8,8);
//将密钥转换为二进制流
Char8ToBit64(keyBlock+i*8,bKey[i]);
//生成子密钥
DES_MakeSubKeys(bKey[i],subKeys[i]);
}
while(1){
memcpy(cipherBlock,cipherBuffer + des_count,8);
for (i = 0; i < 3 ; i++)
{
DES_DecryptBlock(cipherBlock,subKeys[i],plainBlock);
}
if(des_count + 8 < des_size){
memcpy(plainBuffer + des_count,plainBlock,8);
des_count += 8;
} else {
break;
}
}
//判断末尾是否被填充
if(plainBlock[7] < 8){
for(count = 8 - plainBlock[7]; count < 7; count++){
if(plainBlock[count] != '\0'){
break;
}
}
}
if(count == 7){
memcpy(plainBuffer + des_count,plainBlock,8 - plainBlock[7]);
return des_count +8 - plainBlock[7];
} else {
memcpy(plainBuffer + des_count,plainBlock,8);
return des_count +8 ;
}
return des_count + 8;
}
//3DES加密文件
int D3DES_Encrypt_File(char *plainFile, char *keyStr,char *cipherFile){
FILE *plain,*cipher,*key;
ElemType *plainBlock,*cipherBlock,keyBlock[24];
long fileLen_in,fileLen_out;
int count;
if((plain = fopen(plainFile,"rb")) == NULL){
return PLAIN_FILE_OPEN_ERROR;
}
if((key = fopen(keyStr,"rb")) == NULL){
return KEY_FILE_OPEN_ERROR;
}
if((cipher = fopen(cipherFile,"wb")) == NULL){
return CIPHER_FILE_OPEN_ERROR;
}
if((count = fread(keyBlock,sizeof(char),24,key)) == 24){
}
fseek(plain,0,SEEK_END);//将文件指针置尾
fileLen_out = fileLen_in = ftell(plain);//取文件指针当前位置
rewind(plain);//将文件指针重指向文件头
if (fileLen_in % 8 != 0)
fileLen_out = (fileLen_in/8+1)*8;
plainBlock = (ElemType *)malloc(fileLen_out * sizeof(ElemType));
cipherBlock = (ElemType *)malloc(fileLen_out * sizeof(ElemType));
fread(plainBlock,sizeof(char),fileLen_in,plain);
D3DES_Encrypt(plainBlock,keyBlock,cipherBlock,fileLen_in);
fwrite(cipherBlock,sizeof(char),fileLen_out,cipher);
fclose(plain);
fclose(cipher);
fclose(key);
free(plainBlock);
free(cipherBlock);
return DES_OK;
}
//3DES解密文件
int D3DES_Decrypt_File(char *cipherFile, char *keyStr,char *plainFile){
FILE *plain,*cipher,*key;
ElemType *plainBlock,*cipherBlock,keyBlock[24];
int count;
long fileLen_in,fileLen_out;
if((plain = fopen(plainFile,"wb")) == NULL){
return PLAIN_FILE_OPEN_ERROR;
}
if((key = fopen(keyStr,"rb")) == NULL){
return KEY_FILE_OPEN_ERROR;
}
if((cipher = fopen(cipherFile,"rb")) == NULL){
return CIPHER_FILE_OPEN_ERROR;
}
if((count = fread(keyBlock,sizeof(char),24,key)) == 24){
}
fseek(cipher,0,SEEK_END);//将文件指针置尾
fileLen_out = fileLen_in = ftell(cipher);//取文件指针当前位置
rewind(cipher);//将文件指针重指向文件头
plainBlock = (ElemType *)malloc(fileLen_in * sizeof(ElemType));
cipherBlock = (ElemType *)malloc(fileLen_in * sizeof(ElemType));
fread(cipherBlock,sizeof(char),fileLen_in,cipher);
count = D3DES_Decrypt(cipherBlock,keyBlock,plainBlock,fileLen_in);
fwrite(plainBlock,sizeof(char),count,plain);
fclose(plain);
fclose(cipher);
fclose(key);
free(plainBlock);
free(cipherBlock);
return DES_OK;
}
3. 对称加密:AES算法
- 高级加密标准(英语:Advanced Encryption Standard,缩写:AES) ,是美国联邦政府采用的一种
区块加密标准这个标准用来替代原先的DES,已经被多方分析且广为全世界所使用,成为对称密钥加密中最流行的算法之一。 - AES加密数据块分组长度
必须为128比特(16字节),密钥长度可以是128比特、192比特、256比特中的任意一个(如果数据块及密钥长度不足时,会补齐)
/*
* Advanced Encryption Standard
* @author Dani Huertas
* @email [email protected]
*
* Based on the document FIPS PUB 197
*/
#include 4. 非对称加密:RSA算法
- RSA公钥加密算法是1977年由罗纳德-本维斯特( Ron Rivest))、阿迪·萨莫尔
(Adishamir)伦纳德·阿曼德(Leonard Adleman)一起提出的。1987年首次
当时他们三人都行麻省理工学院工作。RSA就是他们兰人姓氏开头字母拼在
起组成的。 - RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的绝大多数密码攻击,被ISO推荐为公钥数据加密标准。
- RSA算法是一种非对称密码算法,所谓非对称,就是指该算法需要一对密钥,使用其中一个加密则需要用另一个才能解密。
- RSA的算法涉及三个参数,n、e1、e2。
- 其中,n是两个
大质数p、q的积(n分解为p,q是数学难题),n的二进制表示时所占用的位数,就是所谓的密钥长度。而且根据n来计算出一次加解密的数据长度。 - e1和e2是一对相关的值,e1可以任意取,但要求
e1与(p-1)**(q-1)互质(没有公因数);再选择e2,要求(e2*e1)mod((p-1)*(q-1))=1.。
- 其中,n是两个
- ( n,e1),(n,e2)就是密钥对。其中(n,e1)为公钥,(n,e2)为私钥。
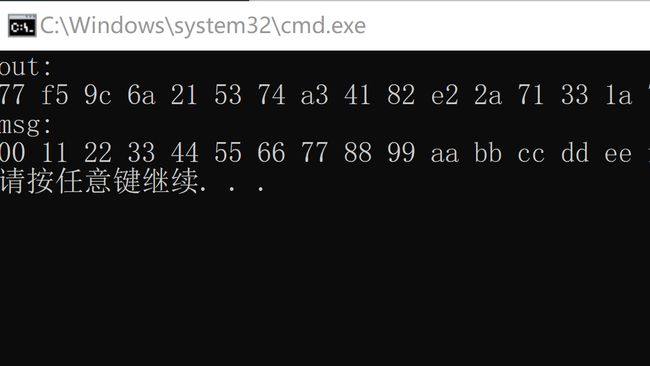
- RSA加解密的算法完全相同,设A为明文,B为密文,则:
#include 5. 基于OpenSSL库的RSA和ASE算法
- OpenSSL (Open Secure Sockets Layer安全套接层)是一个安全套接字层密码库,囊括主要的密码算法、常用的密钥和证书封装管理功能及SSL协议,并提供丰富的应用程序供测试或其它目的使用。
- 由加拿大人Eric A. Young和Tim J.Hudson自1995年开始编写。并产生巨大影响,这是一个没有太多限制的开放源代码的软件包。1998年,OpenSSL项目组接管了OpensSL的开发工作。
- OpenSSL包含一个命令行工具用来完成OpenSSL库中的所有功能。Apache使用它加密’HTTP, OpensSH使用它加密SSH,但是,你不应该只将其作为一个库来使用,它还是一个多用途的、跨平台的密码工具。
- OpenSSL采用C语言作为开发语言,这使得OpenSSL具有优秀的
跨平台性能。OpenSSL整个软件包大概可以分成三个主要的功能部分:SSL协议库、应用程序以及密码算法库。 - OpenssL一共提供了8种对称加密算法,其中7种是
分组加密算法,仅有的一种流加密算法是RC4。这7种分组加密算法分别是AES、DES、Blowfish、CAST、IDEA、RC2、MRC5。OpenSSL一共实现了4种非对称加密算法,包括DH算法、RSA算法、DSA算法和椭圆曲线算法(EC) - OpenSSL曾曝出严重的“心脏流血"漏洞。
编译和使用OpenSSL加解密的方法
准备环境
- 下载并解压openssl源代码
https://www.openssl.org/source/openssl-1.0.2l.tar.gz - 下载并安装ActivePerl
http://downloads.activestate.com/ActivePerl/releases/5.20.2.2002/ActivePerl-5.20.2.2002-MSWin32-x86-64int-299195.msi
并设置perl的安装路径到环境变量Path中。 - 下载并安装nasm
http://www.nasm.us/pub/nasm/releasebuilds/2.11.08/win32/nasm-2.11.08-installer.exe
执行nasm安装目录下的nasmpath.bat(这个文件用于设置nasm的环境变量,如果依然找不到nasm,那么也可以手动设置nasm安装路径到环境变量Path中) - 打开任务栏开始菜单=>所有程序=>打开的VC命令行中切换到openssl解压出来的目录,如:
cd E:\openssl-1.0.2d - 输入
perl Configure VC-WIN32回车执行 - 输入
ms\do_nasm.bat回车执行 - 输入
nmake -f ms\ntdll.mak -a回车执行动态库编译(此为动态链接库,输出目录out32dll) - 输入
nmake -f ms\nt.mak -a回车执行静态库编译(此为静态链接库,输出目录out32) - 运行out32目录中的openssl.exe命令生成公钥和私钥:
- 生成密钥:
openssl genrsa -out test.key 1024 - 生成公钥:
openssl rsa -in test.key -pubout -out test_pub.key
使用openssl
接下来,在VC项目中调用OpenSSL库中的接口:
- 设置OpenSSL的头文件目录:
- 设置OpenSSL的库文件目录:
- 设置OpenSSL的库文件名称:
- 在项目中包含OpenSSL的头文件:
#include "openssl/rsa.h"
#include "openssl/pem.h"
#include "openssl/err.h"
#include "openssl/applink.c"//防止:OPENSSL_Uplink(0098E000,07): no OPENSSL_Applink
然后就可以在项目中使用OpenSSL的接口来进行RSA,AES等加解密了
// openssl-rsa.cpp : Defines the entry point for the console application.
//
#include6. 散列算法:MD5
- MD5Message-Digest Algorithm 5(信息-摘要算法5),用于确保信息传输完整一致。是计算机广泛使用的
哈希算法,将数据运算为另一固定长度值,是哈希算法的基础原理,MD5的前身有MD2、 MD3和MD4。 - MD5算法具有以下特点:
// md5test.cpp : Defines the entry point for the console application.
//
#include "md5c.h"
#include /// md5.h
/* POINTER defines a generic pointer type */
typedef unsigned char * POINTER;
/* UINT2 defines a two byte word */
//typedef unsigned short int UINT2;
/* UINT4 defines a four byte word */
typedef unsigned long int UINT4;
/* MD5 context. */
typedef struct {
UINT4 state[4]; /* state (ABCD) */
UINT4 count[2]; /* number of bits, modulo 2^64 (lsb first) */
unsigned char buffer[64]; /* input buffer */
} MD5_CTX;
void MD5Init (MD5_CTX *context);
void MD5Update (MD5_CTX *context, unsigned char *input, unsigned int inputLen);
void MD5UpdaterString(MD5_CTX *context,const char *string);
int MD5FileUpdateFile (MD5_CTX *context,char *filename);
void MD5Final (unsigned char digest[16], MD5_CTX *context);
void MDString (char *string,unsigned char digest[16]);
int MD5File (char *filename,unsigned char digest[16]);
/// md5.c
/* MD5C.C - RSA Data Security, Inc., MD5 message-digest algorithm
*/
/* Copyright (C) 1991-2, RSA Data Security, Inc. Created 1991. All
rights reserved.
License to copy and use this software is granted provided that it
is identified as the "RSA Data Security, Inc. MD5 Message-Digest
Algorithm" in all material mentioning or referencing this software
or this function.
License is also granted to make and use derivative works provided
that such works are identified as "derived from the RSA Data
Security, Inc. MD5 Message-Digest Algorithm" in all material
mentioning or referencing the derived work.
RSA Data Security, Inc. makes no representations concerning either
the merchantability of this software or the suitability of this
software for any particular purpose. It is provided "as is"
without express or implied warranty of any kind.
These notices must be retained in any copies of any part of this
documentation and/or software.
*/
#include "md5c.h"
#include 三、应用
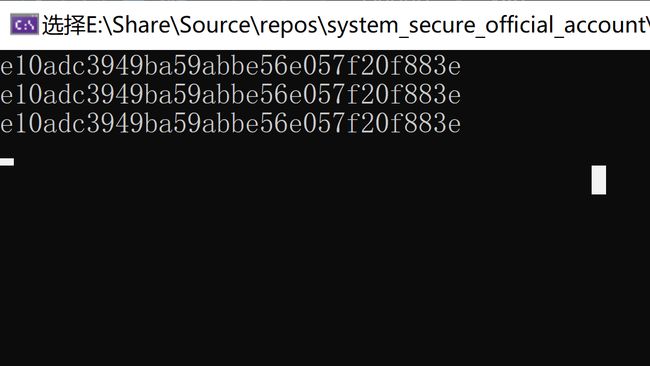
1. 数字签名防篡改
- 计算文件的HASH值(比如MD5值)
- 以
私钥将HASH值加密,然后存储在文件中某个位置(比如头部或者尾部) - 使用的时候,通过
公钥将文件中这个位置的加密数据解密得到HASH值,和文件当前的HASH值进行比对 - 匹配,则文件未被修改;不匹配,文件已被修改
2. 对称与非对称结合加解密
- 对称加密:.快
- 非对称加密:慢
- 对称加密
加密数据+非对称加密加密其密钥
Aeskey_encrypt(data)+publickey_encrypt(aes_key)=发送=>privatekey_decrypt(aes_key)+Aeskey_decrypt(data)