sklearn机器学习之特征选取(feature_selection)
1.导入相应包
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
import numpy as np
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.neighbors import KNeighborsClassifier as KNN
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import f_classif
from sklearn.feature_selection import mutual_info_classif as MIC
2.加载数据集并划分特征和标签
#利用pandas读入数据集
data = pd.read_csv(r"D:\download\sklearnjqxx_jb51\【机器学习】菜菜的sklearn课堂(1-12全课)\03数据预处理和特征工程\digit recognizor.csv")
#标签列为第一列
X = data.iloc[:, 1:]
y = data.iloc[:, 0]
X.shape
此时数据的维度为(42000, 784),可以看到这是一个很恐怖的数字,但是也正很符合当今大数据时代数据之“大”。
3.删除方差为0的特征列
selector = VarianceThreshold()
X_var0 = selector.fit_transform(X)
X_var0.shape
运行结果显示删除方差值为0的特征列后矩阵维度为(42000, 708),这说明特征矩阵中有74列特征的方差值为0。
4.通过方差中位数删除一半的特征列
X_fvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X)
X_fvar.shape
运行后矩阵维度变为(42000, 392),恰好删除一半的特征列。
5.如果特征列服从二项分布
此时我们可以通过概率公式计算方差:
V a r [ X ] = p ( 1 − p ) Var[X] = p(1-p) Var[X]=p(1−p)
我们假设概率为0.8,则有:
X_bvar = VarianceThreshold(0.8 * (1 - 0.8)).fit_transform(X)
X_bvar.shape
输出矩阵维度为(42000, 685)。
6.最后我们选择利用方差中位数为阈值的数据集
X_fsvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X)
X_fsvar.shape
7.接下来利用KNN和随机森林对比效果
#knn算法在数据处理前后的效果
knn_s_1 = cross_val_score(KNN(), X, y, cv=5).mean()
knn_s_2 = cross_val_score(KNN(), X_fsval, y, cv=5).mean()
#随机森林算法在数据处理前后的效果
rfc_s_1 = cross_val_score(RFC(n_estimators=10,random_state=0), X, y, cv=5).mean()
rfc_s_2 = cross_val_score(RFC(n_estimators=10,random_state=0), X_fsvar, y, cv=5).mean()
这里简单介绍一下在一个cell格中记录运行时间的命令
%%timeit
注意:为了计算所需的时间,需要将这个cell中的代码运行很多次(通常是7次)后求平均值,因此运行%%timeit的时间会远远超过cell中的代码单独运行的时间,所以在这种超规模的运算时并不建议。
这里由于电脑运行速度太慢,我们直接拿教程中的数据结果进行比较:
| 原始数据 | 通过方差中位数筛选后的数据 | |
|---|---|---|
| KNN运行时间 | 34min | 20min |
| 随机森林运行时间 | 11.5s | 11.1s |
| KNN精度 | 96.586% | 96.600% |
| 随机森林精度 | 93.800% | 93.881% |
首先可以观察到的是,随机森林的准确率略逊于KNN,但运行时间却连KNN的1%都不到,只需要十几秒钟。其次,方差过滤后,随机森林的准确率也微弱上升,但运行时间却几乎是没什么变化,依然是11秒钟。
为什么随机森林运行如此之快?为什么方差过滤对随机森林没很大的有影响?
这是由于两种算法的原理中涉及到的计算量不同。最近邻算法KNN,单棵决策树,支持向量机SVM,神经网络,回归算法,都需要遍历特征或升维来进行运算,所以他们本身的运算量就很大,需要的时间就很长,因此方差过滤这样的特征选择对他们来说就尤为重要。但对于不需要遍历特征的算法,比如随机森林,它随机选取特征进行分枝,本身运算就非常快速,因此特征选择对它来说效果平平。这其实很容易理解,无论过滤法如何降低特征的数量,随机森林也只会选取固定数量的特征来建模;而最近邻算法就不同了,特征越少,距离计算的维度就越少,模型明显会随着特征的减少变得轻量。因此,过滤法的主要对象是:需要遍历特征或升维的算法们,而过滤法的主要目的是:在维持算法表现的前提下,帮助算法们降低计算成本。
8.对方差过滤后的数据进行相关性过滤
8.1卡方过滤
#chi2表示卡方,这里我们去k=300
X_fschi = SelectKBest(chi2, k=300).fit_transform(X_fsvar, y)
X_fschi.shape
得到最后矩阵维度为(42000, 300)
那么如何获取最好的k呢?
这里我们想起了我们之前的搜索
score = []
#记录每一次的交叉验证精度
for i in range(200, 390, 10):
X_fschi = SelectKBest(chi2, k=i).fit_transform(X_fsvar, y)
one_score = cross_val_score(RFC(n_estimators=5, random_state=0), X_fschi, y, cv=5).mean()
score.append(one_score)
绘制图像
plt.plot(range(200, 390, 10), score)
plt.savefig(r"C:\Users\86377\Desktop\1.png")
plt.show()
得到最后图像为:
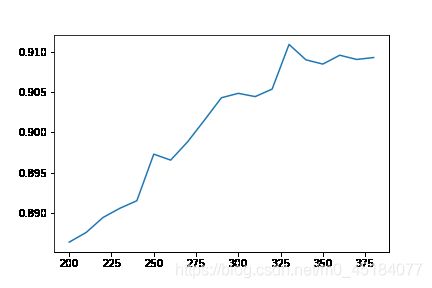
这里我们就可以很清楚选择合适的k值。
但是这样选择耗费的时间成本很大,我们通过显著性>0.05来选取k值:
chivalue, p_valuechi = chi2(X_fsvar, y)
k = chivalue.shape[0] - (p_valuechi > 0.05).sum()
k
最终得到结果k=392,与之前一致,并未发生变化。
8.2F检验
使用方法与卡方检验几乎一致
F, p_valueF = f_classif(X_fsvar, y)
k = F.shape[0] - (p_valueF > 0.05).sum()
k
最终得到结果k=392,与之前一致,并未发生变化。
我们得到结论:没有任何特征的p值大于0.01,所有的特征都是和标签相关的,因此我们不需要相关性过滤。
8.3互信息法
这里和前两者用法有些小差异,这里我们只有一个输出,那就是相关性。
mic = MIC(X_fsvar, y)
k = mic.shape[0] - sum(mic <= 0)
k
得到的结果还是392,说明没有更多的信息去删除。
9.Embedded嵌入法
from sklearn.feature_selection import SelectFromModel
#定义一个随机森林
RFC_ = RFC(n_estimators =10,random_state=0)
#设置阈值为0.005进行筛选
X_embedded = SelectFromModel(RFC_, threshold=0.005).fit_transform(X, y)
X_embedded.shape
最终得到维度为(42000, 47),维度被明显降低了。
但是阈值如何设置呢?
我们采用搜索的方法
#我们在重要程度中
threshold = np.linspace(0, RFC_.fit(X, y).feature_importances_.max(), 20)
score = []
for i in threshold:
X_embedded = SelectFromModel(RFC_, threshold=i).fit_transform(X, y)
one_score = cross_val_score(RFC_, X_embedded, y, cv=5).mean()
score.append(one_score)
plt.plot(threshold, score)
plt.show()
最终得到图像为:
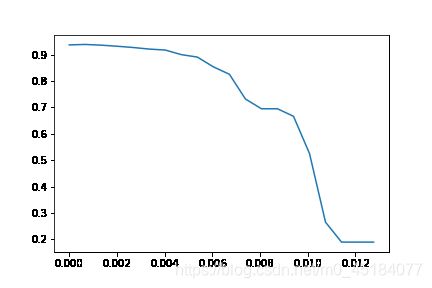
从图像我们看出,随着阈值的不断增大,信息损失的越多,模型拟合的效果越来越差,这里我们可以选择一个更小的范围去获取最大的拟合精度。
9.包装法
from sklearn.feature_selection import RFE
#这里RFC_是模型,n_features_to_select是选择特征的数量,step是每次删除多少特征
selector = RFE(RFC_, n_features_to_select=340, step=50).fit(X, y)
.support_:返回所有的特征的是否最后被选中的布尔矩阵,以及.ranking_返回特征的按数次迭代中综合重要性的排名。
selector.support_
selector.ranking_
获取最后选出的340个特征并训练:
X_wrapper = selector.transform(X)
cross_val_score(RFC_, X_wrapper, y, cv=5).mean()
最终得分为0.93798
可以看到包装法是最能保证模型效果的特征选取方法。
这里我们也可以照样选出最佳的n_features_to_select参数
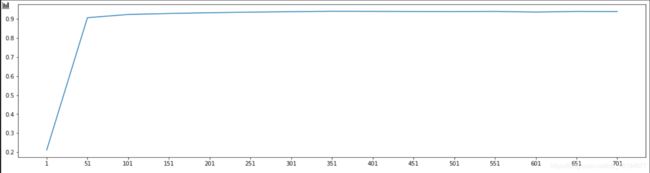
score = []
for i in range(1, 751, 50):
X_wrapper = RFE(RFC_, n_features_to_select=i, step=50).fit_transform(X, y)
one_score = cross_val_score(RFC_, X_wrapper, y, cv=5).mean()
score.append(one_score)
plt.figure(figsize=[20, 5])
plt.plot(range(1, 751, 50), score)
plt.xticks(range(1, 751, 50))
plt.show()
从结果图可以看到随着n_features_to_select参数的增大而增大,而且增大幅度会逐渐变小。