MATLAB中polyval函数用法

目录

语法

说明

示例

计算几个点处的多项式值

对四次多项式求积分

具有误差估计值的线性回归

使用中心化和缩放改善数值属性

---

        polyval函数的功能是多项式计算。

语法

y = polyval(p,x)
[y,delta] = polyval(p,x,S)
y = polyval(p,x,[],mu)
[y,delta] = polyval(p,x,S,mu)

说明

        y = polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量，其元素是 n 次多项式的系数（降幂排序）：

        虽然可以为不同目的使用 polyint、polyder 和 polyfit 等函数计算 p 中的多项式系数，但也可以为系数指定任何向量。要以矩阵方式计算多项式，请改用 polyvalm。

        [y,delta] = polyval(p,x,S) 使用 polyfit 生成的可选输出结构体 S 来生成误差估计值。delta 是使用 p(x) 预测 x 处的未来观测值时的标准误差估计值。

        y = polyval(p,x,[],mu) 或 [y,delta] = polyval(p,x,S,mu) 使用 polyfit 生成的可选输出 mu 来中心化和缩放数据。mu(1) 为 mean(x)，mu(2) 为 std(x)。使用这些值时，polyval 将 x 的中心置于零值处并缩放为具有单位标准差

        这种中心化和缩放变换可改善多项式的数值属性。

示例

计算几个点处的多项式值

        计算多项式 p(x)=3x^2+2x+1在点 x=5,7,9 处的值。多项式系数可以由向量[3 2 1] 表示。

p = [3 2 1];
x = [5 7 9];
y = polyval(p,x)
y = 1×3

    86   162   262

对四次多项式求积分

        计算定积分

        创建一个向量来表示多项式被积函数 项不存在，因此系数为 0。

p = [3 0 -4 10 -25];

        使用 polyint 和等于 0 的积分常量来对多项式求积分。

q = polyint(p)
q = 1×6

    0.6000         0   -1.3333    5.0000  -25.0000         0

        通过在积分范围上计算 q，求解积分的值。

a = -1;
b = 3;
I = diff(polyval(q,[a b]))
I = 49.0667

具有误差估计值的线性回归

        将一个线性模型拟合到一组数据点并绘制结果，其中包含预测区间为 95% 的估计值。

        创建几个由样本数据点 (x,y) 组成的向量。使用 polyfit 对数据进行一次多项式拟合。指定两个输出以返回线性拟合的系数以及误差估计结构体。

x = 1:100; 
y = -0.3*x + 2*randn(1,100); 
[p,S] = polyfit(x,y,1); 

        计算以 p 为系数的一次多项式在 x 中各点处的拟合值。将误差估计结构体指定为第三个输入，以便 polyval 计算标准误差的估计值。标准误差估计值在 delta 中返回。

[y_fit,delta] = polyval(p,x,S);

        绘制原始数据、线性拟合和 95% 预测区间 y±2Δ。

plot(x,y,'bo')
hold on
plot(x,y_fit,'r-')
plot(x,y_fit+2*delta,'m--',x,y_fit-2*delta,'m--')
title('Linear Fit of Data with 95% Prediction Interval')
legend('Data','Linear Fit','95% Prediction Interval')

        如图所示：

使用中心化和缩放改善数值属性

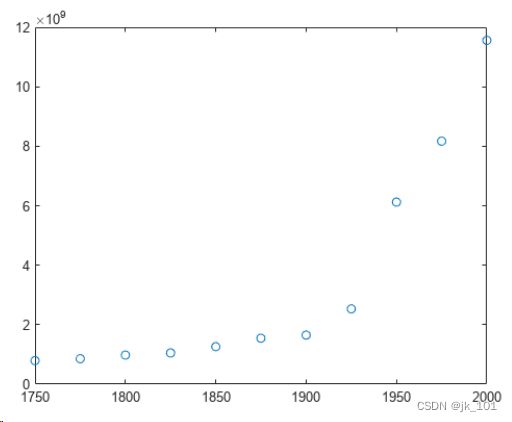
        创建一个由 1750 - 2000 年的人口数据组成的表，并绘制数据点。

year = (1750:25:2000)';
pop = 1e6*[791 856 978 1050 1262 1544 1650 2532 6122 8170 11560]';
T = table(year, pop)
T=11×2 table
    year       pop   
    ____    _________

    1750     7.91e+08
    1775     8.56e+08
    1800     9.78e+08
    1825     1.05e+09
    1850    1.262e+09
    1875    1.544e+09
    1900     1.65e+09
    1925    2.532e+09
    1950    6.122e+09
    1975     8.17e+09
    2000    1.156e+10

plot(year,pop,'o')

如图所示：

        使用带三个输入的 polyfit 拟合一个使用中心化和缩放的 5 次多项式，这将改善问题的数值属性。polyfit 将 year 中的数据以 0 为进行中心化，并缩放为具有标准差 1，这可避免在拟合计算中出现病态的范德蒙矩阵。

[p,~,mu] = polyfit(T.year, T.pop, 5);

        使用带四个输入的 polyval，根据缩放后的年份 (year-mu(1))/mu(2) 计算 p。绘制结果对原始年份的图。

f = polyval(p,year,[],mu);
hold on
plot(year,f)
hold off

        如图所示：

参数说明

p — 多项式系数

        多项式系数，指定为向量。例如，向量 [1 0 1] 表示多项式，向量 [3.13 -2.21 5.99] 表示多项式。

x — 查询点

        查询点，指定为向量。polyval 计算多项式 p 在 x 中的点处的值，并在 y 中返回对应的函数值。

S — 误差估计结构体

        误差估计结构体。此结构体是 [p,S] = polyfit(x,y,n) 的可选输出，可用于获取误差估计值。S 包含以下字段：

字段	描述
R	范德蒙矩阵 x 的 QR 分解的三角因子
df	自由度
normr	残差的范数

        如果 y 中的数据是随机的，则 p 的估计协方差矩阵是 (Rinv*Rinv')*normr^2/df，其中 Rinv 是 R 的逆矩阵。

mu — 中心化值和缩放值

        中心化和缩放值，指定为二元素向量。此向量是 [p,S,mu] = polyfit(x,y,n) 的可选输出，用于改善拟合和计算多项式 p 的数值属性。值 mu(1) 为 mean(x)，mu(2) 为 std(x)。这些值用于以单位标准差将 x 中的查询点的中心置于零值处。

        指定 mu 以计算 p 在缩放点 (x - mu(1))/mu(2) 处的值。

y — 函数值

        函数值，以大小与查询点 x 相同的向量形式返回。向量包含在 x 中的每个点处计算多项式 p 所得的结果。

delta — 预测的标准误差

        预测的标准误差，以大小与查询点 x 相同的向量形式返回。通常，区间 y ± Δ 对应于大型样本的未来观测值约 68% 的预测区间，y ± 2Δ 对应于约 95% 的预测区间。

        如果 p 中的系数是 polyfit 计算的最小二乘估计值，polyfit 数据输入中的误差呈独立正态分布，并拥有常量方差，则 y ± Δ 对应于至少 50% 的预测区间。