C++：【搜索】深度优先搜索与广度优先搜索

在图的搜索中，深度优先搜索（depth-firsrt-serch）和广度优先搜索（breadth-first-seach）是两种非常重要的搜索方式，它们分别对应了对图的不同搜索路径。本文就来介绍一下图的相关知识以及这两种搜索方式。
要学习这两种搜索方式，首先要具备一些图的基本知识，对图不了解的人可以参考一下大佬的文章
数据结构：图(Graph)【详解】

一、深度优先搜索（dfs）

1、dfs介绍

简单来说，dfs就是从图的某一个点开始，沿着一条路走到黑，不撞南墙不回头。在走到尽头的时候，再返回搜索下一条路。举个简单的例子：

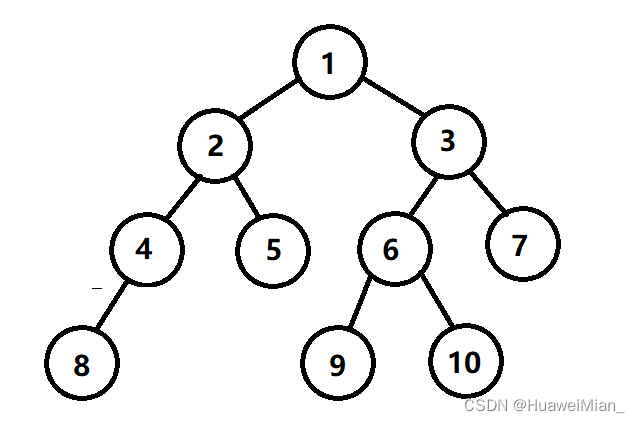
这乍一看好像是一个树，但是其实大部分图都是错综复杂的，树只是一种特殊的图，因为举例子比较方便，所以就先用树状图举例子了。
dfs从1号点开始，假设从最左边这条边开始搜索，那么要搜索到末端，也就是：

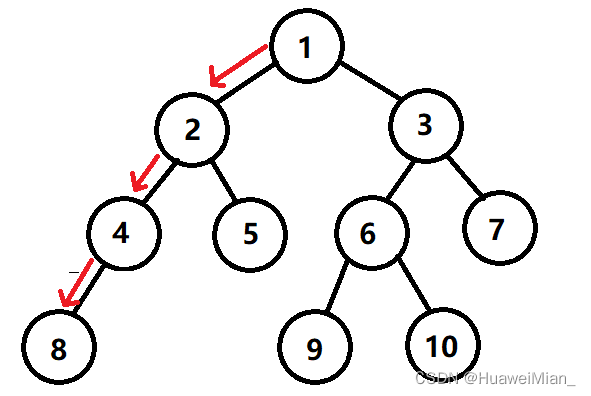
然后就要回头了，那么回到哪里呢？回到离他最近的一个有岔路的点，并从那条岔路一直搜索到末端。也就是：

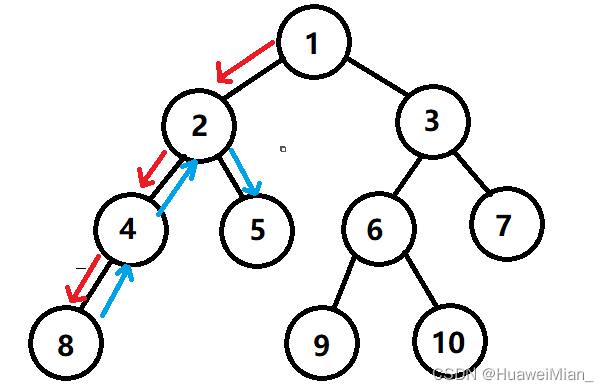
以此类推，直到所有点都被搜索过，也就是出发点的所有出边都被搜索过了，那么就可以结束了。总的来看就是：

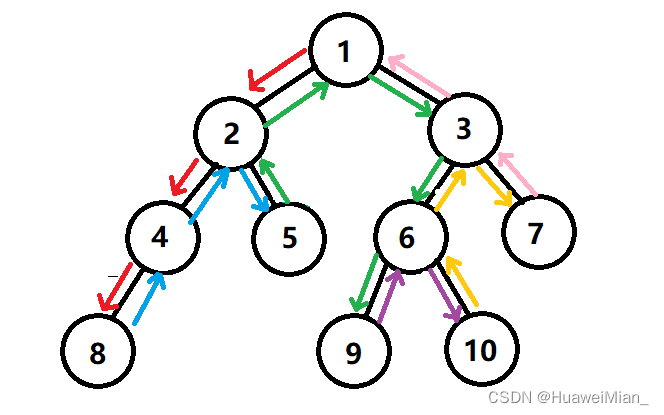
具体路径就是：红 -> 蓝 -> 绿 -> 紫 -> 黄 -> 粉 -> 结束

简单来说，就是一个一搜到底，不撞南墙不回头的过程。这样就可以把一个连通块中的所有点都搜索一遍。dfs就是这样一个过程，现在举两个例子来深入理解一下具体过程。

2、例题.排列数字

原题：acwing排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式
共一行，包含一个整数 n。

输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围
1≤n≤7
输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

对于刚接触搜索的人来说，这道题可能并没有什么头绪。当然经过了长时间的做题积累，很容易就可以明确这是一道dfs题。大致描述一下思路：

1. 要排列数字，首先要从第一位开始，因为是字典序，所以要把数字从小到大填入第一位。
2. 填完第一位后，就要开始填第二位，同样，也要从小到大填入第二位。注意此时要判断一下，因为不能有重复的数字，所以第一位填过的数字就不能填入了。
3. 以此类推，处理后面几位。

了解了大致思路了，来看一下怎么把它抽象为一道dfs。以三个数画个图：

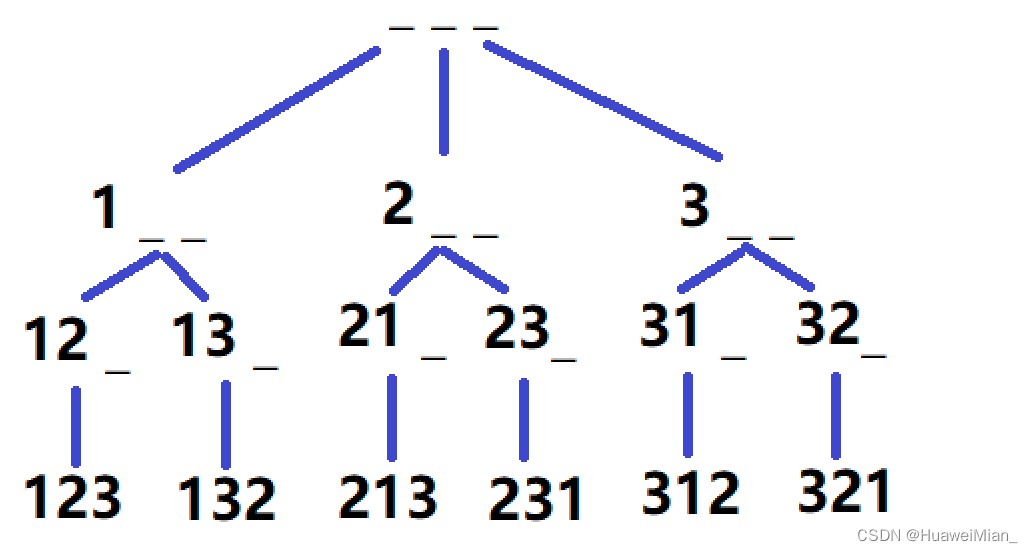
dfs的关键步骤就是回溯，也就是走到一条边的尽头后，如何折返回去。由于dfs的题目要求都比较奇怪，所以没有一个固定的模板，只能说是积累做题经验。
那么这道题目来说，就用函数递归来解决。要检测是否有重复数字，可以设置一个数组表示每个数字的状态，最初设置为0，如果该数字被填充过后就设置为1。
函数的功能是向一个位置填充一个数字，如果填满就返回并打印当前数字，如果未填满就递归调用向下一个位置进行填充。期间要检测当前数字有没有被填充过。
那么接下来处理一下回溯的过程。当走到一条路的尽头以后，在这道题目里也就是每个位置都被填满以后，函数就返回了。也就是：

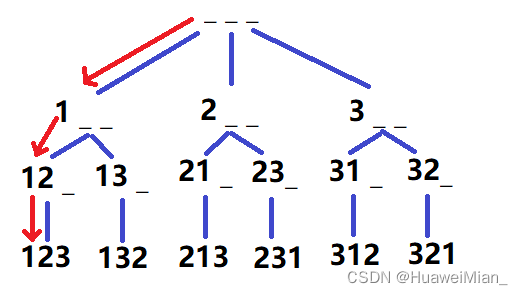
先从12_的位置填入3以后到123的位置，这时候发现填满了，就可以打印输出了，并且返回当前函数调用到12_的位置，注意此时要把3的状态改为未填入，此时发现3以后没有数字可以填入了，所以就再次返回到1_ _的位置，同时把2的状态改为未填入。这时候发现3没被填过，并且之前的数字也没有填过3（因为3的状态为未填过），这时候就可以填入3了，同时把3的状态改为已填入。进入第二条岔路：

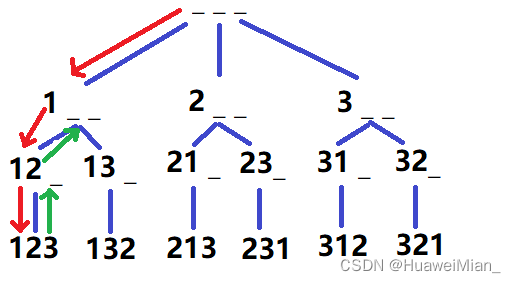
也就是图中绿色的箭头所代表的过程。
这也就实现了回溯。我们可以体会到，其实回溯就是一个恢复作案现场的过程。想要回溯的时候，要把上一步已经确定的状态复原。具体在这道题来说，就是在红色箭头末尾填过3打印后，并回到上一个进程之后，要把3的状态设置为未填过。
以此类推，就可以把所有的情况全部遍历过。

下面给出具体的代码实现：

#include 
#include 

using namespace std;

const int N = 10;

int n;
//st表示每个数的状态
bool st[N];
//path表示当前已经填入的数
int path[N];

//u表示当前已经填入了几个数
void dfs(int u)
{
	//如果填满，就进行打印并返回
    if (u == n)
    {
        for (int i = 0; i < n; i ++ ) cout << path[i] << ' ';
        puts("");
        return;
    }
    
    //遍历每个数，找到符合要求的数
    for (int i = 1; i <= n; i ++ )
    {
        if (!st[i])
        {
        	//如果符合要求（即没被填过），就填入
            path[u] = i;
            //此时把被填入数的状态设置为已填入
            st[i] = true;
            //递归调用填入下一个数
            dfs(u + 1);
            //回溯时要把被填入的数状态设置为为填入，也就是恢复案发现场
            st[i] = false;
        }
    }
}

int main()
{
    cin >> n;
    
    dfs(0);
    
    return 0;
}

总的来看，dfs最难的一点就是回溯。做dfs题目时，应该先构思好每个状态是如何回溯的，只要突破了回溯这一步骤，那么整个题目也就很容易了。

二、广度优先搜索（bfs）

1、bfs介绍

广度优先搜索也叫宽度优先搜索，一般适用于边权相等（也即边的长度）的最短路（有时为最少步骤）问题。bfs是从图的某一个点开始，逐层搜索，先搜索离该点最近的一层，再搜索离该点次近的一层，以此类推直到搜索到最远的一层。举个例子：

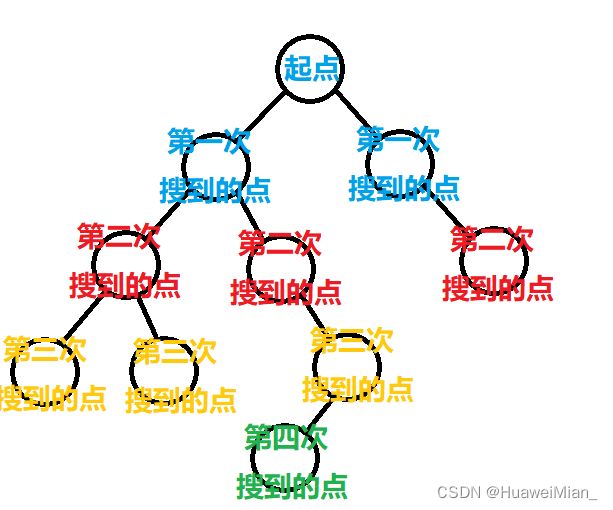
这个例子能很好的解释bfs逐层搜索的过程，也便于理解逐层的含义。通俗来说，就是先近后远的搜索。bfs相较于dfs更加容易理解，因为它不需要回溯，只需要依次搜索距离由近及远的点即可。下面讲述如何实现这样一种由近及远的搜索。
bfs的实现一般是用队列（queue）来实现的。具体来说，就是先让选定的起始点入队，然后通过起点找到离起点最近的点，并且让这些点入队，同时让起点出队（因为起点已经被搜索过），然后通过目前在队列中的这些点（离起点最近的点），找到离这些点最近的点（新找到的这些点也即离起点次近的点），并且让这些点入队，同时让上一波入队的点出队，依次类推直到队列为空（此时所有的点已经被搜索过，因为没有更远的点可以入队了），就能实现由近及远的搜索，同时要注意特别判断一下，已经被搜索过的点就不需要再次入队了。

2、例题.走迷宫

原题：acwing走迷宫

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。
最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

输入格式
第一行包含两个整数 n 和 m。
接下来 n 行，每行包含 m 个整数（0 或 1），表示完整的二维数组迷宫。

输出格式
输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围
1≤n,m≤100
输入样例：

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

8

很明显这是一道边权相等的bfs问题，那么就考虑使用bfs来解决。
本题目较为简单，只给出大致思路：首先读入迷宫，并且开一个和迷宫大小相同的二维数组来存储每个位置到起点的最短距离，最后输出右下角点的距离即可。具体实现为从起点开始逐层搜索，每层搜索到的点距离依次增加，已经搜过的点不需要重复搜索（因为只有最先被搜到的那次搜索才是最短距离）。下面给出注释代码：

#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 110;

//g为迷宫数组，d为每个点到起点的最短距离
int g[N][N], d[N][N];
int n, m;
//q为实现bfs的队列
PII q[N * N];

int bfs()
{
	//初始队列不为空，因为需要起点先入队
    int hh = 0, tt = 0;
    q[0] = {0, 0};
    
    //将所有点的距离设置为-1（不可能的距离），距离值为-1的点代表还未被搜索
    memset(d, -1, sizeof d);
    //起点到起点的距离为0
    d[0][0] = 0;
    
    //小技巧：遇到上下左右移动的问题时，开两个移动数组，并且用数组下标来表示移动方向
    //例如，向右移动为a[x + dx[0]][y + dy[0]]，也即a[x + 0][y + 1]
    int dx[4] = {0, 0, -1, 1}, dy[4] = {1, -1, 0, 0};

	//直到队列为空
    while (hh <= tt)
    {
    	//t为当前点，也即要通过这个点找到离这个点最近的点
        auto t = q[hh ++ ];
        
        //应用上面的小技巧，对四个方向进行搜索，因为本题中离某点最近的点只可能是上下左右
        for (int i = 0; i < 4; i ++ )
        {
            int x = t.first + dx[i], y = t.second + dy[i];
            //判断：当前位置可以走 且 当前位置未被搜索过 且 当前位置没有出界
            if (g[x][y] == 0 && d[x][y] == -1 && x >= 0 && x < n && y >= 0 && y < m)
            {    
            	//距离依次增加
                d[x][y] = d[t.first][t.second] + 1;
                //新的点入队
                q[ ++ tt] = {x, y};
            }
        }
    }
    
    return d[n - 1][m - 1];
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < m; j ++ ) cin >> g[i][j];
        
    cout << bfs() << endl;
    
    return 0;
}