poj 3041 Asteroids （二分图 匈牙利算法）

http://poj.org/problem?id=3041

题意：

给你N*N的矩阵，里面有的方格里有小行星，你需要用激光射掉它。。。激光可以射掉一行 或者一列的小行星，问最小需要发射多少次

 

这道题 很久 以前就做过了  ，现在有做了 一下 ，对 匈牙利 有 个 更好的了解。。。

 

转自 别处 ：

匈牙利算法是寻找最大匹配的优秀算法，那么与这个看上去一点也不像二分图的题来说有什么用处呢？让我们来做一个尝试：把样例数据里面的横坐标作为二分图的一部，纵坐标作为二分图的另一部，坐标为(x, y)的小行星表示为从横坐标x到纵坐标y的一段弧，就有了下图：

 

 

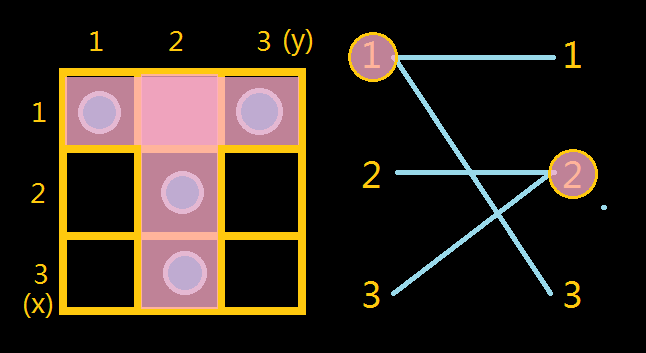
可以看出，原问题变成了下面这个问题：给定一个二分图G = (V, E)，定义一个点如果被覆盖，那么称所有与这个点相邻的弧被覆盖。求出最少需要覆盖多少个点才能覆盖所有的边。如上两个图，原问题中在x = 1和y = 2两处使用超级武器，等价于在右图中覆盖左边的点1和右边的点2。我们称这个问题的答案为最小覆盖数P，显然在样例中P = 2。

现在我们给出结论，若将二分图最大匹配的边集设为M，则P = | M |。也就是最大匹配数。证明如下：

首先证明P ≥ | M | 。对于M中的每一条边，它们都不相邻。那么至少需要覆盖 | M | 个点才能覆盖M中的所有边。故有P ≥ | M | 。

现在给出一种令P = | M |的覆盖方法。如果当前图中对于所有的v ∈ V，都有v ∈ M，显然有P = | M |。否则，任取一条边v0，使v0 ∈ V且v0 ∉ M。那么显然v0的两个端点至少有一个被匹配。

如 果有一端被匹配，设这个端点为a0。首先覆盖a0，然后观察与a0匹配的点a1的状况。如果存在与a1相邻的边v1，满足v1 ∈ V且v1 ∉ M，则v1一定不与没有匹配过的点相邻，否则，v0，v(a0, a1)及v1就形成了增广路。现在继续覆盖与v1相邻的另外一个点a2，然后依次操作，直到新连接到的匹配过的点不与V \ M中的边相邻为止。

如果两端都被匹配，就向两个方向进行同样的操作。从v0的一系列操作结束之后，考察还没有被覆盖的边，继续进行操作。这样最后所有的边一定会被全部覆盖。

如 果说有没有被覆盖到的边，这条边不可能同时与两个匹配过的点相邻。如果这样，在刚才的过程中一定会检索到这条边。所以说它必然是与一个匹配过的点ax相 邻，与一个没有匹配过的点ar相邻，并且ax的匹配点ay一定被覆盖过。那么，从ay向上找寻刚才的过程遍历过的边，与最后的v(ax, ar)一定会形成一条增广路，矛盾。

观察到每条M中的边都有且仅有一个端点被覆盖，所以说P = | M |。

由于P ≥ | M | 且存在P = | M |的状况，故P = | M | ，证明完毕。也就是说，这个题只需要用匈牙利算法求出最大匹配数就可以了。

 

 

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<cmath>
 4 #include<iostream>
 5 #include<algorithm>
 6 #include< set>
 7 #include<map>
 8 #include<queue>
 9 #include<vector>
10 #include< string>
11  #define Min(a,b) a<b?a:b
12  #define Max(a,b) a>b?a:b
13  #define CL(a,num) memset(a,num,sizeof(a));
14  #define eps  1e-12
15  #define inf   0x7fffffff
16 
17  // freopen("data.txt","r",stdin);
18  const  double pi  = acos(- 1.0);
19 typedef   __int64  ll;
20  const  int maxn =  510 ;
21  using  namespace std;
22  int n , m;
23  int mat[maxn][maxn],result[maxn],vis[maxn] ;
24  void init()
25 {
26     memset(mat, 0, sizeof(mat));
27     memset(result, 0, sizeof(result));
28 }
29  int find( int a)
30 {
31      int i;
32      for(i= 1;i<=n;i++)
33     {
34          if(mat[a][i]&&!vis[i])
35         {
36             vis[i]= 1;
37              if(result[i]== 0||find(result[i]))
38             {
39                 result[i]=a;
40                  return  1;
41             }
42         }
43     }
44      return  0;
45 }
46  int main()
47 {
48      int  i ,x,y ;
49      while(scanf( " %d%d ",&n,&m)!=EOF)
50     {
51         init() ;
52          for(i =  0 ; i < m;i++)
53         {
54             scanf( " %d%d ",&x,&y);
55             mat[x][y] =  1;
56 
57         }
58          int ans =  0 ;
59          for(i =  1 ; i<=n;i++ )
60         {
61             CL(vis, 0);
62              if(find(i))ans ++ ;
63         }
64         printf( " %d\n ",ans) ;
65 
66     }
67 }