【代码随想录】算法训练计划02
1、977. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
思路:
这题思路在于——双指针思想
- 简单说就是双指针,左右指针指最外边,谁大放最后边
- 注意条件:i<=j,因为这个元素也要算,加入新数组
// 代码一刷----双指针
func sortedSquares(nums []int) []int {
res := make([]int, len(nums))
k := len(nums)-1
for i,j := 0, len(nums)-1; i<=j; {
if nums[i]*nums[i] > nums[j]*nums[j] {
res[k] = nums[i]*nums[i]
i++
k--
} else {
res[k] = nums[j]*nums[j]
j--
k--
}
}
return res
}
2、209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
思路:
- 滑动窗口,但本质还是双指针法
- j 代表的是终止位置,一旦 sum>=target 就记录最小长度,并把起始位置前移一位
// 代码一刷——双指针——滑动窗口思想
func minSubArrayLen(target int, nums []int) int {
res,sum := 10000000, 0
for i,j := 0,0; j<len(nums); j++ {
sum += nums[j]
for sum >= target {
res = min(res, j-i+1)
sum -= nums[i]
i++
}
}
if res == 10000000 {
return 0
}
return res
}
func min(a,b int) int { if a>b {return b}; return a }
3、59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
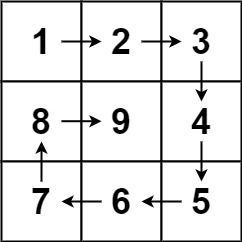
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
思路:
- 这题就是模拟,判断边界条件
- 注意左闭右开法则,保持统一性即可
- 循环次数就是 n/2,如果 n 是奇数就要 center 一下
- 这次写,忘了 i, j := startx, starty 放在循环里边
- 除了 res 外,初始化五个变量,startx,y,offset,count,center
// 代码一刷,循环不变狼——左闭右开规则
func generateMatrix(n int) [][]int {
res := make([][]int, n)
for i:=0; i<n; i++ {
res[i] = make([]int, n)
}
startx,starty := 0,0
offset, count := 1,1
center := n/2
// 开始算法
for k:=0; k<n/2; k++ {
i, j := startx, starty
for ;j<n-offset; j++ {
res[startx][j] = count
count++
}
for ;i<n-offset; i++ {
res[i][j] = count
count++
}
for ; j>startx ; j-- {
res[i][j] = count
count++
}
for ; i>starty ; i-- {
res[i][j] = count
count++
}
offset++
startx++
starty++
}
if n%2 != 0 {
res[center][center] = count
}
return res
}