学习笔记:哈希表及其查找
哈希表及其查找
- 哈希表及其查找
-
- 哈希表
- 哈希函数
-
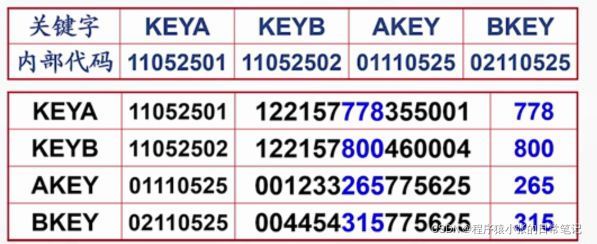
- 1. 直接定址法
- 2. 数字分析法
- 3. 平方取中法
- 4. 折叠法
- 5. 除留余数法
- 6. 随机数法
- 哈希处理冲突方法
-
- 1. 开放定址法
-
- 线性探测再散列 :
- 二次探测再散列:
- 伪随机探测再散列:
- 2. 再散列函数法
- 3. 链地址法
- 4. 公共溢出区法
- 散列表(哈希表)查找的实现
-
- 散列表结构定义:
- 初始化散列表:
- 散列函数:
- 插入关键字进散列表:
- 散列表查找关键字:
- 主函数:
- 运行结果:
- 散列表查找性能的分析:
哈希表及其查找
哈希表
基于线性表的查找法:顺序查找,折半查找
基于树的查找法:二叉排序树,平衡二叉树
特点:记录在表中的位置和关键字间不存在确定关系,查找的过程为给定值依次和各个关键字比较,查找的效率取决进行比较的关键字个数。
这类查找法,平均查找长度都不为零。
若希望ASL=0
方法:预先知道所查关键字在表中的位置 即:记录在表中位置和其关键字之间的确定关系。
在一般情况下,需在关键字与记录在表中的存储位置之间建立一个函数关系,以f(key)作为关键字为key的记录在表中的位置,通常称这个函数f(key)为哈希函数。
通过哈希函数建立的查找表即为哈希表。
哈希函数是一个映像,即:将关键字的集合映射到某个地址集合上。
在一般情况下,容易产生"冲突"现象,key1不等于key2,而f(key1)=f(key2)。
很难找到一个不产生冲突的哈希函数,一般情况下,只能选择恰当的哈希函数,使冲突尽可能少地产生。
哈希表的概念:根据设定的哈希函数H(key)和所选中处理冲突的方法,将一组关键字映像到一个有限的,地址连续的地址集(区间)上,并以关键字在地址集中的"象"作为相应记录在表中的存储位置,如此构造所得的查找表称之为"哈希表"。
哈希函数
哈希函数构造方法:
原则: 1. 函数本身便于计算
2.计算出来的地址分布均匀
若是非数字关键字,则需先对其进行数字化处理。
1. 直接定址法
取关键字的某个线性函数值为散列地址。
f(key) = key 或 f(key) = a*key+b (a,b为常数)
2. 数字分析法
假设关键字集合中的每个关键字都是由s位数字组成(u1,u2,…,u(s)),分析关键字集中的全体,并从中提取分布均匀的若干位或它们的组合作为地址。
3. 平方取中法
以关键字的平方值的中间几位作为存储地址。
不同关键字会以较高的概率产生不同的哈希地址。
4. 折叠法
将关键字分割成若干部分,然后取它们的叠加和为哈希地址。
折叠叠加
移位叠加
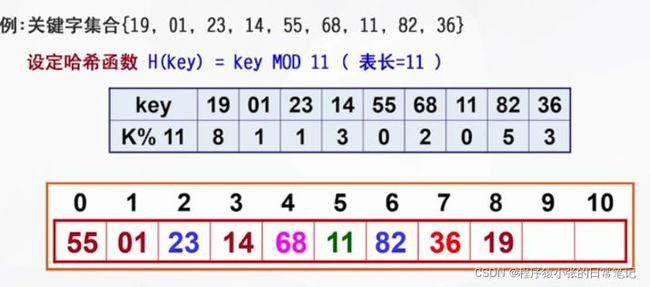
5. 除留余数法
H(key) = key mod p
表长是m,p是<=m的最大素数
6. 随机数法
f(key) = random(key) random是随机函数
总之,现实中,应该视不同的情况采用不同的散列函数。我们只能给出一些考虑的因素来提供参考:
- 计算散列地址所需的实间
- 关键字的长度
- 散列表的大小
- 关键字的分布情况
- 记录查找的频率
哈希处理冲突方法
在哈希表中,尽管构造性能良好的哈希函数可以减少冲突,但实际上冲突是不可避免的。
"处理冲突"是为产生冲突的地址寻找下一个哈希地址。
1. 开放定址法
开放定址法就是一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入。
H0 = H(key)
Hi = (H(key)+di) mod m (i=1,2,3,....,m-1) //再哈希
对增量di有三种取法:
-
线性探测再散列 :
di = c x i 最简单的情况 c=1
哈希函数是对11求余,那如果失败,就意味着失败的所有情况对11求余的结果,可能的范围是0,1…10,一共这11种不同的可能。
当遇到空单元就意味着查找失败了。
-
二次探测再散列:
特点:冲突发生时,在表的右左进行跳跃式探测,比较灵活。
-
伪随机探测再散列:
di=伪随机数列
2. 再散列函数法
准备多个散列函数。
f(key) = Rf(key)
3. 链地址法
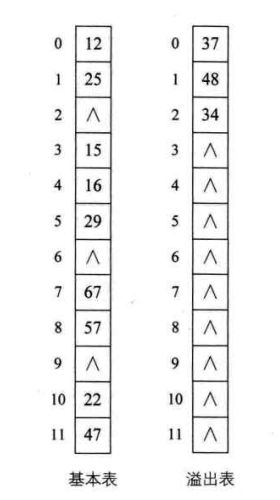
例如:对于关键字集合{12,67,56,16,25,37,22,29,15,47,48,34}
f(key)=key mod 12
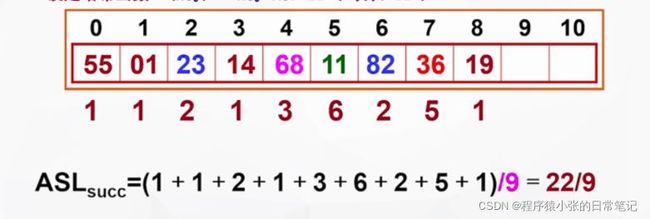
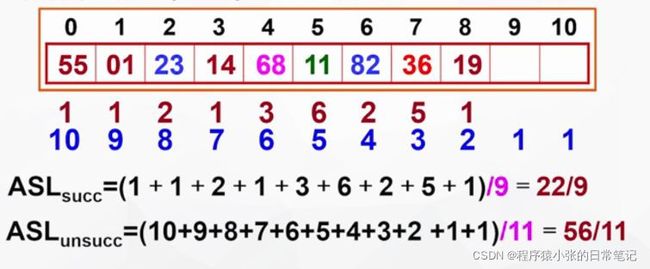
ASL (成功) = (1x9+2x3)/12=15/12
ASL (失败) = (2+2+1+1+1+1+1+2+1)/12=1
4. 公共溢出区法
例如上一个例子,我们共有三个关键字{37,48,34}与之前的关键字位置有冲突,那么就将它们存储到溢出表中
在查找时,对给定值通过散列函数计算出散列地址后,先与基本表的相应位置进行比对,如果相等,则查找成功;如果不相等,则到溢出表去进行顺序查找。
散列表(哈希表)查找的实现
散列表结构定义:
typedef struct
{
int *elem; //数据元素存储基址,动态分配数组
int count; //当前数据元素个数
}HashTable;
初始化散列表:
int m=0; // 散列表表长,全局变量
//初始化散列表
Status InitHashTable(HashTable &H)
{
int i;
m=HASHSIZE;
H.count=m;
H.elem=(int *)malloc(m*sizeof(int));
for(i=0;i<m;i++)
H.elem[i]=NULLKEY;
return OK;
}
散列函数:
int Hash(int key)
{
return key % m; //除留余数法
}
插入关键字进散列表:
void InsertHash(HashTable &H,int key){
int addr = Hash(key); //求散列地址
while (H.elem[addr] != NULLKEY) //如果不为空,则冲突
{
addr = (addr+1) % m; //开放定址法的线性探测
}
H.elem[addr] = key; //直到有空位后插入关键字}
散列表查找关键字:
Status SearchHash(HashTable H,int key,int &addr)
{
addr = Hash(key); //求散列地址
while(H.elem[addr] != key) //如果不为空,则冲突
{
addr = (addr+1) % m; //开放定址法的线性探测
if (H.elem[addr] == NULLKEY || addr == Hash(key)) //如果循环回到原点
return UNSUCCESS; //则说明关键字不存在
}
return SUCCESS;
}
主函数:
#define SUCCESS 1
#define UNSUCCESS 0
#define HASHSIZE 12 /* 定义散列表长为数组的长度 */
#define NULLKEY -32768
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
int main()
{
int arr[HASHSIZE]={12,67,56,16,25,37,22,29,15,47,48,34};
int i,p,key,result;
HashTable H;
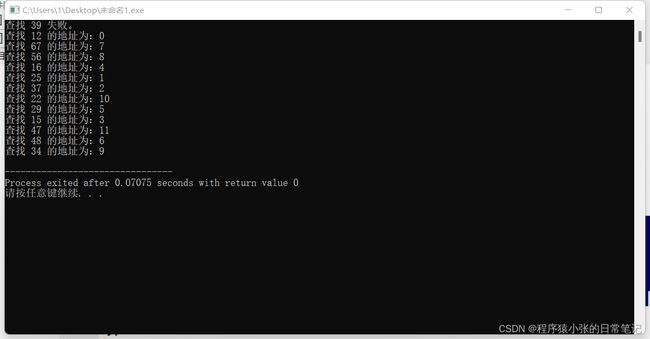
key=39;
InitHashTable(H);
for(i=0;i<m;i++)
InsertHash(H,arr[i]);
result=SearchHash(H,key,p);
if (result)
printf("查找 %d 的地址为:%d \n",key,p);
else
printf("查找 %d 失败。\n",key);
for(i=0;i<m;i++)
{
key=arr[i];
SearchHash(H,key,p);
printf("查找 %d 的地址为:%d \n",key,p);
}
return 0;
}
运行结果:
散列表查找性能的分析:
散列查找是本章中查找效率最高的,它的时间复杂度为O(1)。
散列查找表的平均查找长度取决于
- 散列函数是否均匀
- 处理冲突的方法
- 散列表的装填因子
所谓装填因子a=填入表中的记录个数/散列表的长度。a标志着散列表的装满程度。填入表中的记录越多,a就越大,产生冲突的可能性就越大。