数据结构学习笔记——哈希表
注:本文章的内容大部分摘自由李春葆主编的《数据结构教程》
1、基本概念
哈希表又称散列表,其基本思路是,设要存储的元素个数为n,设置一个长度为m(m>=n)的连续内存单元,以每个元素的关键字ki(0<=i<=n-1)为自变量,通过一个哈希函数 h(ki)将ki映射为内存单元的地址(或下标),并把该元素存储在这个内存单元中,h(ki)成为哈希地址,如此构造的线性表的存储结构为哈希表。
在构建表的时候可能存在这样的问题,两个关键字ki和kj(i != j)且这两个关键字不相等,但会出现映射的地址相同的情况,并把这种情况叫哈希冲突。通常把具有不同关键字而具有相同哈希地址的叫同义词。
2、哈希函数构造方法
1)直接地址法
以关键字k本身或关键字加上某个常量c作为哈希地址的方法。哈希函数为:
![]()
2)除留余数法
用关键字k除以某个不大于哈希表长度m的整数p所得的余数作为哈希地址。哈希函数通常为:
![]()
3)数字分析法
该方法是提取关键字中取值较均匀的数字位作为哈希地址。它适合与所有关键字已知的情况。
3、哈希冲突的解决办法
1)开放地址法
在出现哈希冲突的哈希表中找一个新的空闲位置存放元素。例如要存放关键字为ki的元素,d=h(ki),而地址d的单元已经被其他的元素占据了,那么就在d地址的前后找空闲位置。根据开放地址法找空闲单元的方式又分为线性探测法和平方探测法等。
- 线性探测法
线性探测法是从发生冲突的地址(设为d0)开始,依次探测d0的下一个地址(当到达下标为m-1的哈希表尾时,下一个的探测地址是表首地址0),直到找到一个空闲单元为止(当m>=n时一定能找到空闲单元)。线性探测法的递推描述公式为:
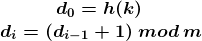
线性探测法的优点是解决冲突简单,一个重大的缺点是容易产生堆积问题。这是由于当连续出现若干个同义词时(设第一个同义词占用单元d0,这连续的若干个同义词将占用哈希表的d0,d0+1,d0+2等单元),随后任何d0+1,d0+2,等单元上的哈希映射都会由于前面的同义词堆积而产生冲突,这些非同义词的冲突,就是哈希函数值不同的两个元素争夺同一个后继哈希地址导致出现的堆积。 - 平方探测法
- 设发生冲突的地址为d0,平方探测法的探测序列为d0+12,
d0-12,d0+22,d0-22,…。其数学描述公式为:
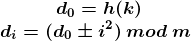
平方探测法是一种较好的处理冲突的方法,可以避免出现堆积的问题。
此外,开方地址法的探测方法还有伪随机序列法,双哈希函数法等。
2)拉链法
拉链法是把所有的同义词用单链表链接起来的方法。,如下图所示,所有哈希地址为 i 的元素对应的节点构成一个单链表,哈希表的地址空间为0~m-1,地址为 i 的单元是一个指向对应单链表的首节点。在这种方法中,哈希表的每个单元中存放的不再是元素本身,而是相应同义词单链表的首节点指针。
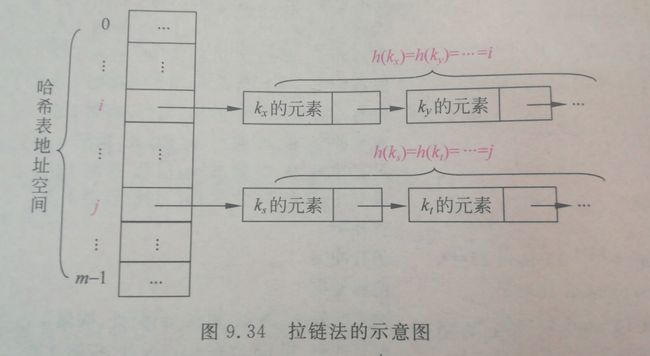
与开放地址法相比,拉链法有以下几个优点:
- 处理冲突简单,无堆积现象,即非同义词绝不会发生冲突,因此平均查找长度较短;
- 由于拉链法中各单链表上的节点空间是动态申请的,它更适合造表前无法确定表长的情况;
- 开放地址法为减少冲突时要求装填因子较小,故当数据规模较大时会浪费很多空间;
- 拉链法删除节点的操作容易实现。
4、解决哈希运算算法
1)线性探测法
- 基本数据结构
#define NULLKEY -1 //定义空关键字
#define DELKEY -2 //定义被删除的关键字
typedef int KeyType;
typedef struct {
KeyType key; //关键字
int count; //探测次数
}HashTable;
//个人感觉增加一个状态位来表明是NULLKEY还是DELKEY要好些,上面的结构中,-1和-2都不能当关键字存储了
- 插入和建表
在建表时首先要将表中各元素关键字清空,使其地址为开放的;然后调用插入算法。将关键字插入到表中,在插入算法中,求出关键字k的哈希地址addr,若该地址可直接存放(即addr位置的关键字为NULLKEY或DELKEY),将其放入;否则出现冲突,采用线性探测法在表中找到一个开放地址,将k插入。若查找次数达到了表最大能存的元素数,则插入失败。
void InsertHT(HashTable ha[], int &n, int m, int p, KeyType k) {
//ha是哈希表的存储空间、n是已存储元素总数,m是哈希表大小,p是哈希函数用的,k是键值
int i, addr;
addr = k%p; //哈希地址
if (ha[addr].key == NULLKEY || ha[addr].key == DELKEY) {
ha[addr].key = k;
ha[addr].count = 1;
}
else {
i = 1;
do {
addr = (addr + i) % m; //线性探测
++i;
} while (ha[addr].key != NULLKEY && ha[addr].key != DELKEY && i < m);
if (i == m){
std::cout << "探测失败" << std::endl;
return;
}
ha[addr].key = k;
ha[addr].count = i; //探测次数
}
++n;
}
void CreateHT(HashTable ha[], int &n, int m, int p, KeyType keys[], int n1) {
//n1是关键字个数
for (int i = 0; i < m; ++i) {
ha[i].key = NULLKEY;
ha[i].count = 0;
}
n = 0;
for (int i = 0; i < n1; ++i)
InsertHT(ha, n, m, p, keys[i]);
}
- 删除
删除,用开放地址法删除时不能简单地将被删除元素的空间置为空,否则将截断在它后面填入哈希表的同义词元素的查找路径,因为在开放地址法中,空地址是查找失败的条件,因此只能在被删除元素上做删除标记DELKEY,而不能真正删除元素
bool DeleteHT(HashTable ha[], int &n, int m, int p, KeyType k) {
int addr;
addr = k%p;
int i = 1;
while (ha[addr].key != NULLKEY && ha[addr].key != k && i < m){
addr = (addr + i) % m;
++i;
}
if (ha[addr].key == k) {
ha[addr].key = DELKEY;
return true;
}
else
return false;
}
- 查找
void SearchHT(HashTable ha[], int m, int p, KeyType k) {
int i = 1, addr;
addr = k%p;
while (ha[addr].key != NULLKEY && ha[addr].key != k && i < m) {
++i;
addr = (k + i) % m;
}
if (ha[addr].key == k)
std::cout << "查找成功,addr:" << addr << std::endl;
else
std::cout << "查找失败" << std::endl;
}
- 性能分析
void ASL1(HashTable ha[], int n, int m, int p) {
int i, j;
int suc = 0, unsuc = 0, s;
for (i = 0; i < m; ++i)
//查找成功的直接计算count和就行
if (ha[i].key != NULLKEY && ha[i].key != DELKEY)
suc += ha[i].count;
std::cout << "查找成功平均比较次数: " << suc / n << std::endl;
for (i = 0; i < p; ++i) {
s = 1; j = 1;
//当遇到第一个NULLKEY就表示查找失败
while (ha[i].key != NULLKEY) {
++s;
j = (j + 1) % m;
}
unsuc += s;
}
std::cout << "查找不成功平均比较次数: " << unsuc / p << std::endl;
}