分治算法④-使用分治算法实现最近点对问题-python
该问题指的是:在一个平面上,有着许多的散点,如果找出欧式距离最近的两个点。从问题表面可以看出,该问题可以用暴力法求解,即求出所有点之间的距离,再统一进行比较,选出距离最近的点对。但这样做,难免时间复杂度较高,所以就需要用别的解法来计算,常用的是分治法:即按X坐标或Y坐标将元素区分成两部分,然后不断划分,直到每个子区间中只有一个元素,求出左右区间中最小点对之间的距离,这样就求出了两个区间最小值。接下来要求出最复杂的第三个最小值:两个点在不同的子区间,如何在不同区间寻找这两个点就成了最近点对问题的难点。
此问题的解决步骤,参考了网上一篇比较容易理解的文章:算法设计与分析——分治法:详解二维最近点对问题,具体步骤如下:
1>选择所有点的某一坐标(X坐标或Y坐标,此处以X轴为例),求出平均值,划分中轴线,将数据按某一坐标轴分为左右两个部分。
2>求出左半边和右半边的最小距离,选取较小值d,此步骤可以用递归实现。
3>根据上一步求出的d,求出最小点对在不同区间时的最小距离。
4>比较这三个最小距离。
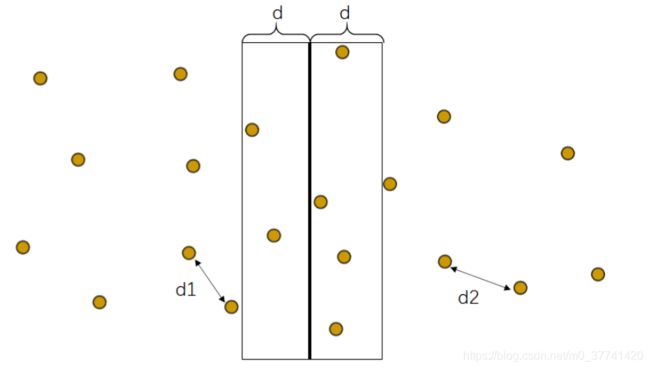
上述步骤中,较难理解的部分是第3步。首先在左右区间各选择一个点时,肯定是在某个区域中选择时,这个区域的宽度如何定义。正确的做法应该是
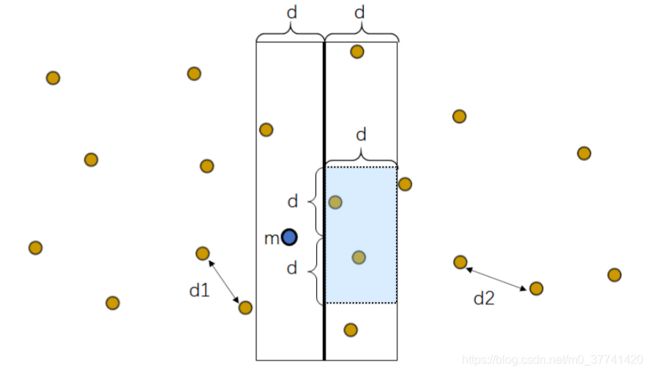
d1和d2分别为左右区间中最小点对之间的距离,d为d1和d2的较小值。 接下来就要确定区域的高度范围了,这个范围不是固定的,需要根据每次选择的点来动态设置。假设我们在左半边选择了一个点,那这个点对应的Y轴坐标的2d之间的高度就是高度范围,因为2d之外的点与当前选择点之间的距离也肯定>d,如下:
算法实现-python:
'''
最小点对算法:给定平面上n个点,找其中的一对点,使得在n个点的所有点对中,该点对的距离最小。严格地说,最接近点对可能多于1对。为了简单起见,这里只限于找其中的一对。
主要算法思想:先把所有点按照x值排序,从最中间(x值中位数b)将所有点分为三个部分,左子域(左子域包括中间子域)、右子域、x值恰好等于中位数的中间子域,分别找出左右子域中的最近点,取最小值为d,
再将左右子域的x值范围缩减到[b-d,b+d]之间,循环遍历左子域中的每个点,在右子域中寻找y值离当前点最近的四个点,分别求距离,取最小距离,然后寻找中间子域中的最近点,取最小距离
通过递归(分治)的方法,最终正确查找到最近点对
'''
import math
# 输入
p = [[0, 0], [1, 1], [3, 4], [0, 3], [3.2, 4.2], [0, -1], [-2, -2], [-1, -2], [0, 0.4], [-1, 2], [0, 2], [0.5, 2]]
# p = [[0,0], [1,1], [3,4]]
n = len(p)
# 预期输出:最近点对是 ( 3.2 , 4.2 ) 和 ( 3 , 4 ), 最短距离为 0.2828427124746193
# 查找最接近的目标的y下标
def find_closed_index(collections, target):
n = len(collections)
low = 0
high = n - 1
mid = 0
while low <= high:
mid = math.floor((low + high) / 2)
if target > collections[mid][1]:
low = mid + 1
elif target < collections[mid][1]:
high = mid - 1
else:
return mid
return mid
def distance(p1, p2):
return math.sqrt(pow(p1[0] - p2[0], 2) + pow(p1[1] - p2[1], 2))
def divide(l, r, res):
if l == r:
return float("inf"), []
if (l + 1) == r:
return distance(p[l], p[r]), [p[l], p[r]]
mid = math.floor((l + r) / 2)
d1, res1 = divide(l, mid, res)
d2, res2 = divide(mid + 1, r, res)
if d1 >= d2:
d = d2
res = res2
else:
d = d1
res = res1
# 先将所有左子域、右子域、同一x值的中间子域,删选出来
left = []
right = []
midd = []
b = p[mid][0]
bl = b - d
br = b + d
for i in range(n):
if ((p[i][0] >= bl) & (p[i][0] <= b)) == True:
left.append(p[i])
if p[i][0] == b:
midd.append(p[i])
elif ((p[i][0] <= br) & (p[i][0] >= b)) == True:
right.append(p[i])
if len(right) == 0:
return d, res
# 将右子域先按照y值大小排好序
right.sort(key=lambda x: x[1])
# 遍历左子域中的每一个点,在右子域中寻找y值最邻近的四个点,求出最小距离以及最近点对
for i in range(len(left)):
closed_point = []
right_num = len(right)
if right_num <= 4:
closed_point = right
else:
index = find_closed_index(right, left[i][1])
if index >= 4:
start = index - 4
else:
start = 0
if index + 5 > len(right) - 1:
end = len(right) - 1
else:
end = index + 5
for j in range(start, end):
closed_point.append(right[j])
# 前四个就是右子域中离左子域最近的四个点
closed_point.sort(key=lambda x: abs(x[1] - left[i][1]))
if len(closed_point) >= 4:
end2 = 4
else:
end2 = len(closed_point)
for k in range(0, end2):
dist = distance(closed_point[k], left[i])
if dist < d:
res = [closed_point[k], left[i]]
d = dist
# 再在中间子域的内部进行比较,看看有没有x值相同,且距离最近的两个点
if len(midd) > 1:
midd.sort()
for j in range(len(midd) - 1):
dist = distance(midd[j], midd[j + 1])
if dist < d:
res = [midd[j], midd[j + 1]]
d = dist
return d, res
# 前期需要按照x值排序
p.sort()
d, res = divide(0, n - 1, [])
print("最近点对是 (", res[0][0], ",", res[0][1], ") 和 (", res[1][0], ",", res[1][1], "), 最短距离为", d)