Java实现回溯算法入门（排列+组合+子集）
算法相关数据结构总结：
| 序号 | 数据结构 | 文章 |
|---|---|---|
| 1 | 动态规划 | 动态规划之背包问题——01背包 动态规划之背包问题——完全背包 动态规划之打家劫舍系列问题 动态规划之股票买卖系列问题 动态规划之子序列问题 算法（Java）——动态规划 |
| 2 | 数组 | 算法分析之数组问题 |
| 3 | 链表 | 算法分析之链表问题 算法（Java）——链表 |
| 4 | 二叉树 | 算法分析之二叉树 算法分析之二叉树遍历 算法分析之二叉树常见问题 算法（Java）——二叉树 |
| 5 | 哈希表 | 算法分析之哈希表 算法（Java）——HashMap、HashSet、ArrayList |
| 6 | 字符串 | 算法分析之字符串 算法（Java）——字符串String |
| 7 | 栈和队列 | 算法分析之栈和队列 算法（Java）——栈、队列、堆 |
| 8 | 贪心算法 | 算法分析之贪心算法 |
| 9 | 回溯 | Java实现回溯算法入门（排列+组合+子集） Java实现回溯算法进阶（搜索） |
| 10 | 二分查找 | 算法（Java）——二分法查找 |
| 11 | 双指针、滑动窗口 | 算法（Java）——双指针 算法分析之滑动窗口类问题 |
文章目录
-
-
- 1. 从全排列问题开始理解回溯算法
-
- 46.全排列
- 47.全排列 II
- 2.组合问题的回溯算法
-
- 39.组合总和
- 40.组合总和 II
- 216.组合总和Ⅲ
- 77.组合
- 3.子集问题
-
- 78.子集
- 90.子集Ⅱ
- 4.排列组合问题的总结
-
回溯是递归的副产品，只要有递归就会有回溯，所以回溯法也经常和二叉树遍历，深度优先搜索混在一起，因为这两种方式都是用了递归。
回溯法 采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：
- 找到一个可能存在的正确的答案；
- 在尝试了所有可能的分步方法后宣告该问题没有答案。
回溯法就是暴力搜索，并不是什么高效的算法，最多再剪枝一下。
回溯算法能解决如下问题：
- 组合问题：N个数里面按一定规则找出k个数的集合
- 排列问题：N个数按一定规则全排列，有几种排列方式
- 切割问题：一个字符串按一定规则有几种切割方式
- 子集问题：一个N个数的集合里有多少符合条件的子集
- 棋盘问题：N皇后，解数独等等
用回溯三部曲来分析回溯算法，回溯法的模板：
void backtracking(参数){
if(终止条件){
存放结果;
return;
}
for(选择：本层集合中元素（树中节点孩子的数量就是集合的大小）){
处理节点;
backtracking(路径，选择列表);
回溯，撤销处理结果;
}
}
1. 从全排列问题开始理解回溯算法
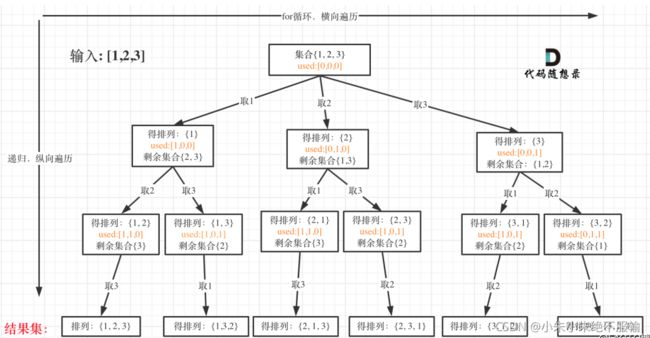
我们尝试在纸上写 3 个数字、4 个数字、5 个数字的全排列，相信不难找到这样的方法。以数组 [1, 2, 3] 的全排列为例。
- 先写以 1 开头的全排列，它们是：[1, 2, 3], [1, 3, 2]，即 1 + [2, 3] 的全排列（注意：递归结构体现在这里）；
- 再写以 2 开头的全排列，它们是：[2, 1, 3], [2, 3, 1]，即 2 + [1, 3] 的全排列；
- 最后写以 3 开头的全排列，它们是：[3, 1, 2], [3, 2, 1]，即 3 + [1, 2] 的全排列。
总结搜索的方法：**按顺序枚举每一位可能出现的情况，已经选择的数字在 当前 要选择的数字中不能出现。**按照这种策略搜索就能够做到 不重不漏。这样的思路，可以用一个树形结构表示。
看到这里的朋友，建议先尝试自己画出「全排列」问题的树形结构。
说明：
- 每一个结点表示了求解全排列问题的不同的阶段，这些阶段通过变量的「不同的值」体现，这些变量的不同的值，称之为「状态」；
- 使用深度优先遍历有「回头」的过程，在「回头」以后， 状态变量需要设置成为和先前一样 ，因此在回到上一层结点的过程中，需要撤销上一次的选择，这个操作称之为「状态重置」；
- 深度优先遍历，借助系统栈空间，保存所需要的状态变量，在编码中只需要注意遍历到相应的结点的时候，状态变量的值是正确的，具体的做法是：往下走一层的时候，path 变量在尾部追加，而往回走的时候，需要撤销上一次的选择，也是在尾部操作，因此 path 变量是一个栈；
- 深度优先遍历通过「回溯」操作，实现了全局使用一份状态变量的效果。
使用编程的方法得到全排列，就是在这样的一个树形结构中完成 遍历，从树的根结点到叶子结点形成的路径就是其中一个全排列。
设计状态变量
- 首先这棵树除了根结点和叶子结点以外，每一个结点做的事情其实是一样的，即：在已经选择了一些数的前提下，在剩下的还没有选择的数中，依次选择一个数，这显然是一个 递归 结构；
- 递归的终止条件是： 一个排列中的数字已经选够了 ，因此我们需要一个变量来表示当前程序递归到第几层，我们把这个变量叫做 depth，或者命名为 index ，表示当前要确定的是某个全排列中下标为 index 的那个数是多少；
- 布尔数组 used，初始化的时候都为 false 表示这些数还没有被选择，当我们选定一个数的时候，就将这个数组的相应位置设置为 true ，这样在考虑下一个位置的时候，就能够以 O(1)的时间复杂度判断这个数是否被选择过，这是一种「以空间换时间」的思想。
这些变量称为「状态变量」，它们表示了在求解一个问题的时候所处的阶段。需要根据问题的场景设计合适的状态变量。
46.全排列
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例一：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]
代码实现：
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
if(nums.length == 0){
return res;
}
Deque<Integer> path = new ArrayDeque<>(); // 用栈去构造path,存储已经选了哪些数
boolean[] used = new boolean[nums.length]; // 用一个used数组判断是否被用过
dfs(nums, 0, path, used, res); // 递归每一层
return res;
}
private void dfs(int[] nums, int depth, Deque<Integer> path, boolean[] used, List<List<Integer>> res){
if(depth == nums.length){ // 当遍历的层数等于数组长度时结束
res.add(new ArrayList<>(path)); // 将path的拷贝加入到res中，就不会出现多余的空列表，要注意
return;
}
for(int i = 0; i < nums.length; i++){
if(used[i]){
continue; // 如果使用过，则跳出
}
path.addLast(nums[i]);
used[i] = true;
dfs(nums, depth+1, path, used, res); // 遍历下一层
path.removeLast(); //回溯，回到上一层结点
used[i] = false;
}
}
}
说明：
状态变量：
- depth，递归到第几层，这里就是数组的长度。
- path，已经选了哪些数，需要回溯撤销，所以用栈实现，Java中推荐使用Deque构建栈。
- used，布尔数组，判断哪些选择过了。
还需要注意的一点是：
if(depth == nums.length){ // 当遍历的层数等于数组长度时结束
res.add(new ArrayList<>(path)); // 将path的拷贝加入到res中，就不会出现多余的空列表，要注意
return;
}
如果直接将path加入到res中，就会出现错误：
if (depth == len) {
res.add(path);
return;
}
变量 path 所指向的列表 在深度优先遍历的过程中只有一份 ，深度优先遍历完成以后，回到了根结点，成为空列表。
在 Java 中，参数传递是 值传递，对象类型变量在传参的过程中，复制的是变量的地址。这些地址被添加到 res 变量，但实际上指向的是同一块内存地址，因此我们会看到空的列表对象。解决的方法很简单，在 res.add(path); 这里做一次拷贝即可。
47.全排列 II
给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。
示例 1：
输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]
思路是：在遍历的过程中，一边遍历一遍检测，在一定会产生重复结果集的地方剪枝。
剪枝
- 回溯算法会应用「剪枝」技巧达到以加快搜索速度。有些时候，需要做一些预处理工作（例如排序）才能达到剪枝的目的。预处理工作虽然也消耗时间，但能够剪枝节约的时间更多；
如果要比较两个列表是否一样，一个容易想到的办法是对列表分别排序，然后逐个比对。既然要排序，我们就可以 在搜索之前就对候选数组排序，一旦发现某个分支搜索下去可能搜索到重复的元素就停止搜索，这样结果集中不会包含重复列表。
画出树形结构如下：重点想象深度优先遍历在这棵树上执行的过程，哪些地方遍历下去一定会产生重复，这些地方的状态的特点是什么？
对比图中标注 ① 和 ② 的地方。相同点是：这一次搜索的起点和上一次搜索的起点一样。不同点是：
- 标注 ① 的地方上一次搜索的相同的数刚刚被撤销；
- 标注 ② 的地方上一次搜索的相同的数刚刚被使用。
产生重复结点的地方，正是图中标注了「剪刀」，且被绿色框框住的地方。
大家也可以把第 2 个 1 加上 ’ ，即 [1, 1’, 2] 去想象这个搜索的过程。只要遇到起点一样，就有可能产生重复。这里还有一个很细节的地方：
- 在图中 ② 处，搜索的数也和上一次一样，但是上一次的 1 还在使用中；
- 在图中 ① 处，搜索的数也和上一次一样，但是上一次的 1 刚刚被撤销，正是因为刚被撤销，下面的搜索中还会使用到，因此会产生重复，剪掉的就应该是这样的分支。
代码实现方面，在第 46 题的基础上，要加上这样一段代码：
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
这段代码就能检测到标注为 ① 的两个结点，跳过它们。
具体代码实现：
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
if(nums.length == 0){
return res;
}
// 排序（升序或者降序都可以），排序是剪枝的前提
Arrays.sort(nums);
Deque<Integer> path = new ArrayDeque<>(); // 用栈去构造path,存储已经选了哪些数
boolean[] used = new boolean[nums.length]; // 用一个used数组判断是否被用过
dfs(nums, 0, path, used, res); // 递归每一层
return res;
}
private void dfs(int[] nums, int depth, Deque<Integer> path, boolean[] used, List<List<Integer>> res){
if(depth == nums.length){ // 当遍历的层数等于数组长度时结束
res.add(new ArrayList<>(path)); // 将path的拷贝加入到res中，就不会出现多余的空列表，要注意
return;
}
for(int i = 0; i < nums.length; i++){
if(used[i]){
continue; // 如果使用过，则跳出
}
// 剪枝条件：i > 0 是为了保证 nums[i - 1] 有意义
// 写 !used[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
path.addLast(nums[i]);
used[i] = true;
dfs(nums, depth+1, path, used, res); // 遍历下一层
path.removeLast(); //回溯，回到上一层结点
used[i] = false;
}
}
}
2.组合问题的回溯算法
39.组合总和
给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。
示例 1：
输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]
示例 2：
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3：
输入: candidates = [2], target = 1
输出: []
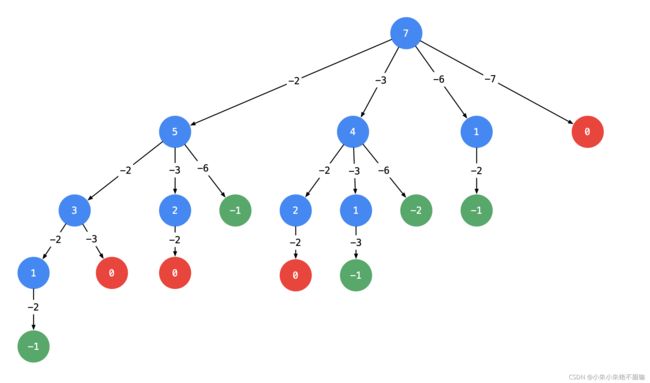
以输入：candidates = [2, 3, 6, 7], target = 7 为例：
说明：
- 以 target = 7 为 根结点 ，创建一个分支的时 做减法 ；
- 每一个箭头表示：从父亲结点的数值减去边上的数值，得到孩子结点的数值。边的值就是题目中给出的 candidate 数组的每个元素的值；
- 减到 0 或者负数的时候停止，即：结点 0 和负数结点成为叶子结点；
- 所有从根结点到结点 0 的路径（只能从上往下，没有回路）就是题目要找的一个结果。
这棵树有 4 个叶子结点的值 0，对应的路径列表是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]]，而示例中给出的输出只有 [[7], [2, 2, 3]]。即：题目中要求每一个符合要求的解是 不计算顺序 的。下面我们分析为什么会产生重复。
产生重复的原因是：在每一个结点，做减法，展开分支的时候，由于题目中说 每一个元素可以重复使用，我们考虑了 所有的 候选数，因此出现了重复的列表。
遇到这一类相同元素不计算顺序的问题，我们在搜索的时候就需要 按某种顺序搜索。具体的做法是：每一次搜索的时候设置 下一轮搜索的起点 begin，请看下图。
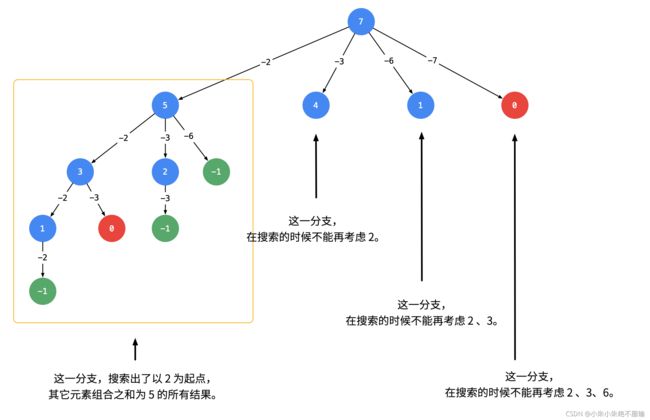即：从每一层的第 2 个结点开始，都不能再搜索产生同一层结点已经使用过的 candidate 里的元素。
剪枝提速：
- 根据上面画树形图的经验，如果 target 减去一个数得到负数，那么减去一个更大的树依然是负数，同样搜索不到结果。基于这个想法，我们可以对输入数组进行排序，添加相关逻辑达到进一步剪枝的目的；
- 排序是为了提高搜索速度，对于解决这个问题来说非必要。但是搜索问题一般复杂度较高，能剪枝就尽量剪枝。
什么时候使用 used 数组，什么时候使用 begin 变量
有些朋友可能会疑惑什么时候使用 used 数组，什么时候使用 begin 变量。这里为大家简单总结一下：
- 排列问题，讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为不同列表时），需要记录哪些数字已经使用过，此时用 used 数组；
- 组合问题，不讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为相同列表时），需要按照某种顺序搜索，此时使用 begin 变量。
代码实现：
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
if(candidates.length == 0){
return res;
}
// 排序是剪枝的前提
Arrays.sort(candidates);
Deque<Integer> path = new ArrayDeque<>();
dfs(candidates, 0, target, path, res);
return res;
}
public void dfs(int[] candidates, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
// 小于0的被剪枝，一次递归的终止条件值只判断等于0的情况
if(target == 0) {
res.add(new ArrayList<>(path));
return;
}
for(int i = begin;i < candidates.length;i++) {
// 前提候选数组有序，然后剪枝
if(target - candidates[i] < 0){
break;
}
path.addLast(candidates[i]);
dfs(candidates, i, target - candidates[i], path, res);
path.removeLast();
}
}
}
40.组合总和 II
给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
注意：解集不能包含重复的组合。
示例一：
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例二：
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
这道题与上一问的区别在于：
- 第 39 题：candidates 中的数字可以无限制重复被选取；
- 第 40 题：candidates 中的每个数字在每个组合中只能使用一次。
相同点是：相同数字列表的不同排列视为一个结果。
如何去掉重复的集合（重点）：
为了使得解集不包含重复的组合。有以下 2 种方案：
- 使用 哈希表 天然的去重功能，但是编码相对复杂；
- 不重复就需要按 顺序 搜索， 在搜索的过程中检测分支是否会出现重复结果 。注意：这里的顺序不仅仅指数组 candidates 有序，还指按照一定顺序搜索结果。
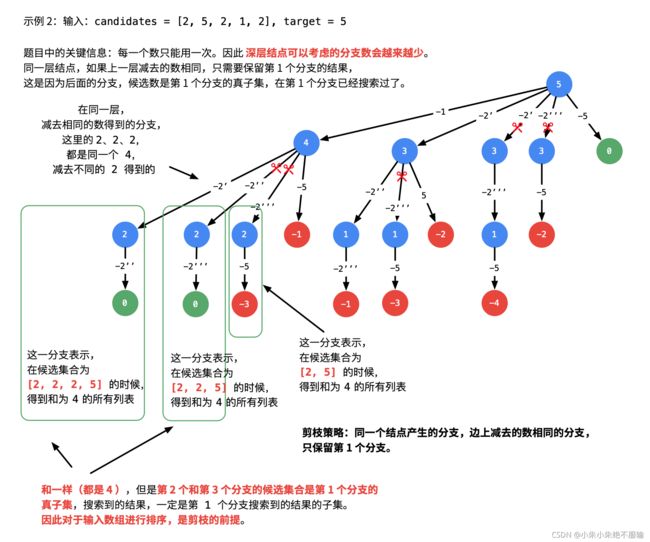由第 39 题我们知道，数组 candidates 有序，也是 深度优先遍历 过程中实现「剪枝」的前提。
将数组先排序的思路来自于这个问题：去掉一个数组中重复的元素。很容易想到的方案是：先对数组 升序 排序，重复的元素一定不是排好序以后相同的连续数组区域的第 1 个元素。也就是说，剪枝发生在：同一层数值相同的结点第 2、3 … 个结点，因为数值相同的第 1 个结点已经搜索出了包含了这个数值的全部结果，同一层的其它结点，候选数的个数更少，搜索出的结果一定不会比第 1 个结点更多，并且是第 1 个结点的子集。
与39题相似，只是增加了一段去重的过程：
// 小剪枝：同一层相同数值的结点，从第 2 个开始，候选数更少，结果一定发生重复，因此跳过，用 continue
if (i > begin && candidates[i] == candidates[i - 1]) {
continue;
}
同时要注意的是：回溯的时候因为元素不能重复使用，递归传递下去的begin变量是i+1而不是 i
// 因为元素不可以重复使用，这里递归传递下去的是 i + 1 而不是 i
dfs(candidates, i+1, target - candidates[i], path, res);
代码实现：
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
if(candidates.length == 0){
return res;
}
Arrays.sort(candidates);
Deque<Integer> path = new ArrayDeque<>();
dfs(candidates, 0, target, path, res);
return res;
}
private void dfs(int[] candidates, int begin, int target, Deque<Integer> path, List<List<Integer>> res){
if(target == 0){
res.add(new ArrayList<>(path));
return;
}
for(int i = begin;i < candidates.length;i++) {
// 前提候选数组有序，然后剪枝
if(target - candidates[i] < 0){
break;
}
// 小剪枝：同一层相同数值的结点，从第 2 个开始，候选数更少，结果一定发生重复，因此跳过，用 continue
if (i > begin && candidates[i] == candidates[i - 1]) {
continue;
}
path.addLast(candidates[i]);
// 因为元素不可以重复使用，这里递归传递下去的是 i + 1 而不是 i
dfs(candidates, i+1, target - candidates[i], path, res);
path.removeLast();
}
}
}
216.组合总和Ⅲ
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。
示例一：
输入: k = 3, n = 7
输出: [[1,2,4]]
示例二：
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
分析：
首先与之前的组合问题雷同。
不同点是，这里限制组合中的元素个数，且不允许元素重复。
终止条件加上限制组合中的元素个数的代码：
if(n == 0 && path.size() == k){ // 终止条件为和等于n且path的size为k
res.add(new ArrayList<>(path));
return;
}
不允许元素重复，则递归还是i+1。
代码实现：
class Solution {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> res = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
int[] can = new int[9];
for(int i = 0; i < 9; i++){ // 构造数组
can[i] = i+1;
}
dfs(can, k, 0, n, path, res);
return res;
}
public void dfs(int[] can, int k, int begin, int n, Deque<Integer> path, List<List<Integer>> res){
if(n == 0 && path.size() == k){ // 终止条件为和等于n且path的size为k
res.add(new ArrayList<>(path));
return;
}
for(int i = begin; i < can.length; i++) {
// 剪枝
if(n - can[i] < 0){
break;
}
path.addLast(can[i]);
dfs(can, k, i+1, n - can[i], path, res); // i+1保证没有重复的
path.removeLast();
}
}
}
77.组合
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
示例一：
输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例二：
输入：n = 1, k = 1
输出：[[1]]
分析：
终止条件：
//终止条件就是path的元素个数为k
path.size() == k
剪枝：
事实上，如果 n = 7, k = 4，从 555 开始搜索就已经没有意义了，这是因为：即使把 5 选上，后面的数只有 6 和 7，一共就 3 个候选数，凑不出 4 个数的组合。因此，搜索起点有上界，这个上界是多少，可以举几个例子分析。
搜索起点和当前还需要选几个数有关，而当前还需要选几个数与已经选了几个数有关，即与 path 的长度相关。
// 剪枝，搜索起点的上界 = n - (k - path.size()) + 1
int i = begin; i <= n - (k - path.size()) + 1; i++
代码实现：
class Solution {
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> res = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
dfs(n, k, 1, path, res); // 不用构造数组,直接传递n,题目是从1开始的
return res;
}
public void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res){
if(path.size() == k){ //终止条件就是path的元素个数为k
res.add(new ArrayList<>(path));
return;
}
// 剪枝，搜索起点的上界 = n - (k - path.size()) + 1
for(int i = begin; i <= n - (k - path.size()) + 1; i++) {
path.addLast(i); //直接把i加进去即可
dfs(n, k, i+1, path, res); // i+1保证没有重复的
path.removeLast();
}
}
}
3.子集问题
78.子集
给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
示例一：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例二：
输入：nums = [0]
输出：[[],[0]]
子集和组合都是无关顺序的，因此是一类问题。
终止条件：
子集问题比较特殊，所有路径都应该加入结果集，所以不存在终止条件，或者说，当递归时begin参数超过数组边界的时候，程序就自己跳过下一层递归了，因此不需要写终止条件，直接加入结果集。
判断是否需要剪枝：
从递归中可以看到没有重复的，也没有不符合条件的，所以不需要剪枝。
只要是每个元素用一次的，都是递归 i+1。
代码实现：
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
if(nums.length == 0){
return res;
}
Deque<Integer> path = new ArrayDeque<>();
dfs(nums, 0, path, res);
return res;
}
private void dfs(int[] nums, int begin, Deque<Integer> path, List<List<Integer>> res){
res.add(new ArrayList<>(path));
// if(begin > nums.length){ // 已经在for循环之外了，可以不需要加了
// return;
// }
for(int i = begin;i < nums.length;i++){
path.addLast(nums[i]);
dfs(nums, i+1, path, res);
path.removeLast();
}
}
}
90.子集Ⅱ
给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。
示例一：
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例二：
输入：nums = [0]
输出：[[],[0]]
分析：
本题与78.子集不同的地方是，给出的数组中含有重复元素，所以会有大量重复的集合，所以需要先对数组排序进行剪枝。
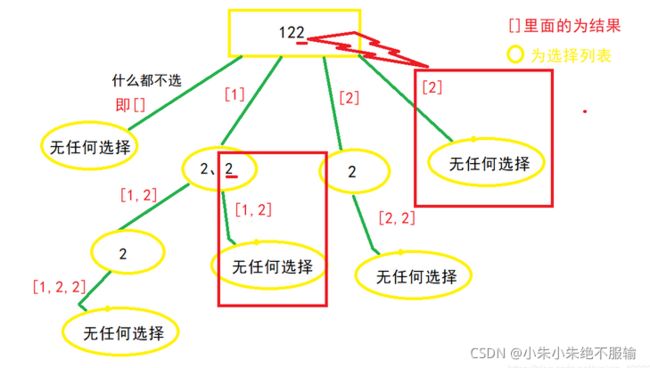
与上题相比只需要添加一段剪枝的代码（先对数组进行排序）：
// 剪枝，重复元素
if(i > begin && nums[i] == nums[i-1]){
continue;
}
代码实现：
class Solution {
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
if(nums.length == 0){
return res;
}
Arrays.sort(nums);
Deque<Integer> path = new ArrayDeque<>();
dfs(nums, 0, path, res);
return res;
}
private void dfs(int[] nums, int begin, Deque<Integer> path, List<List<Integer>> res){
res.add(new ArrayList<>(path));
// if(begin > nums.length){ // 已经在for循环之外了，可以不需要加了
// return;
// }
for(int i = begin;i < nums.length;i++){
// 剪枝，重复元素
if(i > begin && nums[i] == nums[i-1]){
continue;
}
path.addLast(nums[i]);
dfs(nums, i+1, path, res);
path.removeLast();
}
}
}
4.排列组合问题的总结
回溯问题的题型主要分为三种：
- 子集、组合
- 全排列
- 搜索
排列组合问题是回溯算法的基础。
注意：子集、组合与排列是不同性质的概念。子集、组合是无关顺序的，而排列是和元素顺序有关的，如 [1，2] 和 [2，1] 是同一个组合(子集)，但 [1,2] 和 [2,1] 是两种不一样的排列！！！！因此被分为两类问题。
所有问题的解题步骤都是：
- 构建状态变量，path，存储列表，这里用栈去实现。全排列问题使用布尔数组used去判断哪些元素被用过，组合问题使用begin变量去确定搜索顺序。
- 进入回溯，首先确定终止条件，然后判断是否需要剪枝，再然后进入递归（判断递归的循环）。
重要的剪枝问题：
1.组合、子集问题，相同元素不计算顺序的问题，在搜索的时候就需要 按某种顺序搜索，方法是每一次搜索的时候设置 下一轮搜索的起点 begin：for(int i = begin;i < candidates.length;i++)
2.题目中给出的元素是否重复：
有重复元素的话，需要剪枝，方法是先对数组进行排序，在剪枝条件中判断：
- 排列问题判断：
i > 0 && nums[i] == nums[i - 1] && !used[i - 1]； - 组合问题判断：
i > begin && candidates[i] == candidates[i - 1]。
参考：
回溯算法入门级详解 + 练习
一篇总结带你彻底搞透回溯算法！