数据结构学习笔记（第二章：线性表）

2.1 线性表的概念

线性表的定义

• 一个线性表是n个数据元素的有限序列。
• 在稍微复杂的线性表中，一个数据元素可以由若干个数据项 组成。在这种情况下，数据元素也叫做记录，含有大量记录的线性表也叫做文件。

线性结构的特点

• “第一个”数据元素是唯一的，一个线性表中不可能拥有两个“第一个”数据元素。
• 存在唯一的“最后一个”数据元素，线性表不能有两个不同的结尾。
• 除了“第一个”数据元素以外，线性表中每个数据元素都只有一个前驱。
• 除了“最后一个”数据元素以外，线性表中每个数据元素都只有一个后驱

2.2 顺序表（顺序存储）

顺序表的定义

线性表的顺序表：指的是用一组地址连续的存储单元依次存储线性表的数据元素。
顺序表是一种支持随机存取的存储结构。根据起始地址加上元素的序号，可以很方便的访问任意一个元素，这就是随机存取的概念。
它的特点是：每一个数据元素的存储位置都和线性表的起始位置相差一个和数据元素在线性表中的排序成正比的常数，该常数为数据元素的大小。假设该起始位为LOC(L);

数据元素	存储位置
a1	LOC(L)
a2	LOC(L)+1*数据元素的大小
a3	LOC(L)+2*数据元素的大小
…	…

顺序表的实现（C++实现）

在这里，我用c++实现的主要原因是我想要和严蔚敏教材上的内容更为贴近，用&作为形参和教材上提供的算法更像，所以我采用了C++实现。修改成C语言也很容易，但要注意，下面函数的形参不能是带取地址符&的，C语言中没有这样的语法，得换成指针才能用。取地址符作为形参是C++的用法，被称为‘别名’。
下面是定义顺序表的全部代码：

#include 	//C++头文件格式，如果需要可替换成C语言的头文件
using namespace std;

#define list_init_size 100	//初始容量
#define list_increment 10	//线性表存储空间
#define error -1	//因为C语言中没有true和false关键字，虽然C++里有但是这里还是额外定义一下
#define FALSE 0
#define TRUE 1
typedef int elemtype;	//定义数据元素类型，这样做的好处是想要修改类型时只需修改这句话就可以了
typedef int status;	//因为C语言编译器中一般不存在bool,所以这里的定义相当于C++的bool类型，代表函数返回的状态

struct sqlist{
	elemtype *elem;	//存储空间的基址指针
	int length;		//当前顺序表的长度
	int listsize;	//当前分配的空间大小
};

status initlist_sq(sqlist &l){	//顺序表初始化
	l.elem=(elemtype*)malloc(list_init_size*sizeof(elemtype));
	//malloc函数返回申请到的连续空间的基址地址，格式是(申请空间类型*)malloc(申请空间大小)
	if(!l.elem)	return error;//如果申请失败，返回error信号
	l.length=0;
	l.elem[0]=0;//这里为了方便下面的操作，放弃了第0号空间
	l.listsize=list_init_size;
	return TRUE;
}
status destroylist_sq(sqlist &l){	//释放顺序表
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	free(l.elem);
	l.length=0;
	l.listsize=0;
	return TRUE;
}
status clearlist_sq(sqlist &l){	//清空线性表
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	l.length=0;	//顺序表的长度为0就能直接清空了
	return TRUE;
}
status listempty_sq(sqlist &l){	//线性表是否为空，为空则返回TRUE，不空则返回FALSE
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	if(l.length==0)	return TRUE;	//顺序表的长度为0则该线性表为空表
	else return FALSE;
}
int listlength_sq(sqlist &l){	//返回线性表的数据元素个数;
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	return l.length;
}
status get_elem_sq(sqlist l,int i,elemtype &e){	//将线性表l中的第i个数据元素的值赋回给e
	if(!l.elem&&l.length>i)	return error;//初始条件：线性表L和L的第i个元素已经存在
	e=l.elem[i];	//将数据元素赋值给e
	return TRUE;
}
int locate_elem_sq(sqlist l,elemtype e){//返回线性表l中第一个与e相同的的数据元素的位置，如果不存在返回0
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	int i,n=0;
	for(i=1;i<=l.length;i++){
		if(l.elem[i]==e)
		{
			n=i;
			break;
		}
	}
	return n;
}
status prior_elem_sq(sqlist l,elemtype cur_e,elemtype &pre_e){	//求前驱函数，在线性表l返回cur_e的前驱并赋值给pre_e
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	int i,n=0;
	for(i=1;i<=l.length;i++){
		if(l.elem[i]==cur_e)
		{
			n=i-1;
			break;
		}
	}
	if(n==0){	//如果为首个数据元素或者cur_e不存在返回错误信号
		return error;
	}
	else{
		pre_e=l.elem[n];
	}
	return TRUE;
}
status next_elem_sq(sqlist l,elemtype cur_e,elemtype &next_e){	//求后继函数，在线性表l返回cur_e的后一个数据元素并赋值给next_e
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	int i,n=0;
	for(i=1;i<=l.length-1;i++){
		if(l.elem[i]==cur_e)
		{
			n=i+1;
			break;
		}
	}
	if(n==0){	//如果为最后一个数据元素或者cur_e不存在返回错误信号
		return error;
	}
	else{
		next_e=l.elem[n];
	}
	return TRUE;
}
status listinsert_sq(sqlist &l,int i,elemtype e){//在线性表l中的第i个位置之前插入新的数据元素e，l的长度加一
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	if(l.length+1<i||i<1)	return error;//在L线性表中，这个第i位置前还有没有赋值的数据元素，这种情况无法正常赋值。
	if(l.length>=l.listsize){//如果表的空间已满，则需要增加表分配的空间
		elemtype *newbaser=(elemtype *)realloc(l.elem,((l.listsize+list_increment)*sizeof(elemtype)));//realloc函数是重新申请函数对malloc申请的空间进行调整，这段代码的意思是给l.elem的数据元素搬个更大的家
		if(!newbaser)return error;	//申请存储空间失败，返回错误信号
		l.elem=newbaser;//将搬家的新地址登记回来
		l.listsize+=list_increment;	//修改之前登记的家的信息
	}
	l.length++;
	int k;
	for(k=l.length;k>=i+1;k--){
		l.elem[k]=l.elem[k-1];
	}
	l.elem[i]=e;
	return TRUE;
}
status listdelete_sq(sqlist &l,int i,elemtype &e){//删除线性表l第i个数据元素，并用e返回其值，l的长度减一
	int k;
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	if(l.length<i||i<1)	return error;//在L线性表中，这个第i位置还有没有赋值的数据元素，这种情况无法正常删除。
	//开始从后向前替代
	l.length--;
	for(k=i;k<=l.length;k++){
		l.elem[k]=l.elem[k+1];
	}
	
	return TRUE;
}
status list_traverse_sq(sqlist l){//遍历线性表，将线性表中的所有数据元素查看一遍
	if(!l.elem)	return error;//初始条件：线性表L已经存在
	for(int i=1;i<=l.length;i++){
		cout<<l.elem[i]<<" ";
		//C++的输出语句，不需要写变量的格式控制，如果要改成C语言的printf，要注意格式控制符，应该和elemtype保持一致
	}
	printf("\n");
	return TRUE;
}

int main()
{
	int sign;	//接收函数信号
	sqlist s;
	sign=initlist_sq(s);
	if(sign==-1){
		printf("This (initlist_sq) was wrong!\n");	//错误信号处理;
	}
	
	//....
	
	sign=destroylist_sq(s);
	if(sign==-1){
		printf("This (destroylist) was wrong!\n");
	}
	
	return 0;
}

顺序表的简单应用

• 应用一：假设两个线性表 LA 和 LB 分别代表集合 $A$ 和集合 $B$ ，现要求求一个新的集合 $A=A\cup B$，请你利用顺序表设计一个算法：

void union_l(sqlist &la,sqlist lb){
	//la=la U lb
	int lenga,lengb;
	lenga=listlength_sq(la);
	lengb=listlength_sq(lb);
	elemtype e;
	int sign;
	for(int i=1;i<=lengb;i++){
		get_elem_sq(lb,i,e);//因为是la=la U lb，所以检查lb是不是有元素不在la里的即可，没有就插入，有就不做操作
		if(locate_elem_sq(la,e)==0){//必须找不到该元素才可以插入la表中
			listinsert_sq(la,++lenga,e);//插入到尾部，注意使用++lenga，因为插入函数是插入到第i个之前的元素前，所以插到尾部应该是表长度+1的位置之前
		}
	}
	return;
}

• 应用二：已知线性表 LA 和 LB 中的数据元素按值非递减有序排列，先要求将 LA 和 LB 归并为一个新的线性表 LC ，且 LC 中的数据元素扔按值非递减有序数列排序，例如: LA={3,5,8,11},LB={2,6,8,9,11,15,20}，则LC={2,3,5,6,8,8,9,11,11,15,20}，求设计算法：

void mergelist_sq(sqlist la,sqlist lb,sqlist &lc){
	//线性表LA和LB中的数据元素按值非递减有序排列，将LA和LB归并为一个新的线性表LC，且LC中的数据元素扔按值非递减有序数列排序
	initlist_sq(lc);
	int i,j,k=0;
	int lengla=listlength_sq(la);
	int lenglb=listlength_sq(lb);
	for(i=j=1;i<=lengla&&j<=lenglb;){
		elemtype ea,eb;
		get_elem_sq(la,i,ea);
		get_elem_sq(lb,j,eb);
		if(ea>eb){
			listinsert_sq(lc,++k,eb);
			j++;//如果选了lb中的元素则lb进入下一个元素进行比较
		}
		else{
			listinsert_sq(lc,++k,ea);
			i++;//如果选了la中的元素则la进入下一个元素进行比较
		}
	}
	for(;i<=lengla;i++){//查看一下la是否已经全部选完，没有选完则直接将la剩下的元素赋到lc的最后
		elemtype ea;
		get_elem_sq(la,i,ea);
		listinsert_sq(lc,++k,ea);
	}
	for(;j<=lenglb;j++){//查看一下lb是否已经全部选完，没有选完则直接将la剩下的元素赋到lc的最后
		elemtype eb;
		get_elem_sq(lb,j,eb);
		listinsert_sq(lc,++k,eb);
	}	
	return;
}

• 应用三：假设顺序表中的数据元素类型是int型，求从有序顺序表中删除其值在给定值s与t之间（包含s和t，要求s

status delete_1(sqlist &l,int s,int t){
	if(l.length==0||t<s)	return error;	//线性表L不存在,或者s和t的取值不合理，返回错误信号
	int i,j;//因为是有序顺序表，所以s-t之间肯定是截一段数据段，用i标记数据段头，j标记数据段尾
	for(i=1;i<=l.length;i++){
		if(l.elem[i]>=s){
			break;
		}
	}
	for(j=i+1;j<=l.length;j++){
		if(l.elem[j]>t){
			break;
		}
	}
	int k=j-i;
	for(;j<=l.length;j++,i++){
		l.elem[i]=l.elem[j];
	}
	l.length-=k;
	return TRUE;
}

• 应用三：假设顺序表中的数据元素类型是int型，求从顺序表中删除其值在给定值s与t之间（包含s和t，要求s

思考：从头到尾扫描线性表，用k来记录符合删除要求的个数，对于当前扫描到的元素，如果不符合删除要求，则将其移动到前k个位置。

status delete_2(sqlist &l,int s,int t){
	if(l.length==0||t<s)	return error;	//线性表L不存在,或者s和t的取值不合理，返回错误信号
	int i,k=0;
	for(i=1;i<=l.length;i++){
		if(l.elem[i]<=t&&l.elem[i]>=s){
			k++;
		}
		else{
			l.elem[i-k]=l.elem[i];
		}
	}
	l.length-=k;
	return TRUE;
}

• 应用四：已知在一维数组中A[n+m]中依次存放两个线性表$(a_1,a_2...a_n)$和$(b_1,b_2...b_m)$，试编写一个函数，将数组中两个顺序表的位置互换，即把$(b_1,b_2...b_m)$放在$(a_1,a_2...a_n)$前面，要求优先空间复杂度和时间复杂度达到最优解。

思考：一开始我就想着开一组数组临时存放，然后直接交换不就好了，但是因为追求空间复杂度，所以这题就不能这么写了，我们应该先将A[m+n]的全部元素逆置，得到
$(b_m,...,b_2,b_1,a_n,...,a_2,a_1)$，然后再分别将前m个元素和后n个元素原地逆置，即可得到$(b_1,b_2...b_m,a_1,a_2...a_n)$
（忽然发现这题是2010统考题一题的稍微变形题，不过答案都不用变）

status reversal_sq(sqlist &l,int begin,int length){
	//反转函数，将线性表l的从begin的位置将长度为length的数据转置
	if(!l.elem||begin+length-1>l.length){
		return error;
	}
	int mid=begin+(length-1)/2;//找到中间位
	int right=begin+length-1;
	for(int left=begin;left<=mid;left++,right--){
		//将left和right的元素交换
		int t=l.elem[left];
		l.elem[left]=l.elem[right];
		l.elem[right]=t;
	}
	return TRUE;
}
void f(sqlist &l,int n,int m){
	reversal_sq(l,1,l.length);
	reversal_sq(l,1,m);
	reversal_sq(l,m+1,n);
}

2.3 线性链表（链式存储）

线性链表的定义

线性表的链式存储定义是：用一组任意的存储单元存储线性表的数据元素。
它的特点是：

• 插入或删除时，不需要像顺序存储一样，移动其他元素，但是也失去了顺序表可随意读取数据元素内容的特点；
• 每个数据元素$a_i$除了存储自己本身的信息，还有一个指示其直接后继的信息，这两部分组成了数据元素$a_i$的存储映像，称为结点。
• 整个链表的存取必须从头指针开始进行，由于最后一个数据元素没有直接后继，示意图最后一个结点的指针为空（NULL）
  

线性链表的实现（C++实现）

这里我遇到了一个关于定义结构体的小问题，在严蔚敏的数据结构书中是这样写结构体的。

typedef struct lnode{
	elemtype data;
	struct lnode *next;
}lnode,*linklist;

我发现这其实是将结构体struct和typedef类型定义语句组合了起来。
这句话其实可以换成

struct lnode{
	elemtype data;
	struct lnode *next;
};//定义结构体
typedef lnode lnode,*linklist;//将结构体结点重命名

值得注意的是：因为 typedef 语句可以掩饰复合类型，如指针和数组。当经常用到需要申请相同类型的指针或者相同大小的数组时，就可以这样定义，例如

typedef int temp[100];
temp a;

这样执行申请到的a其实是int[100]数组。
所以在这里教材中为了方便的申请到指针使代码更加规范，这里采用了重命名方式将*lnode重新命名为linklist类型。
下面是定义链表的全部代码：

#include 
using namespace std;

#define error -1	//因为C语言中没有true和false关键字，虽然C++里有但是这里还是额外定义一下
#define FALSE 0
#define TRUE 1
typedef int elemtype;	//定义数据元素类型，这样做的好处是想要修改类型时只需修改这句话就可以了
typedef int status;	//因为C语言编译器中一般不存在bool,所以这里的定义相当于C++的bool类型，代表函数返回的状态

struct lnode{
	elemtype data;
	struct lnode *next;
};//定义结构体
typedef lnode lnode,*linklist;//将结构体结点重命名

status createlist_l_head(linklist &l,int n){	//用头插法初始化链表,并建立n个基本数据
	//因为是头插法，所以要求输入的数据应该是倒序，也就是从表尾输入到表头
	l=(linklist)malloc(sizeof(lnode));//申请一个头结点
	//malloc函数格式是(申请空间类型*)malloc(申请空间大小)，linklist等同于*lnode所以这里前面直接使用linklist即可
	if(!l) return error;	//如果申请失败，返回error信号
	l->next=NULL;	//设置头结点的指针为空，现在的链表还是空链表
	for(int i=1;i<=n;i++){
		linklist q=(linklist)malloc(sizeof(lnode));
		q->next=NULL;
		cin>>q->data;	//C++的输入流语句
		q->next=l->next;//头插法将新的数据每次都插在表头
		l->next=q;	//因为表头插入了新元素，所以新元素则为新的表头
	}
	return TRUE;
}
status createlist_l_tail(linklist &l,int n){//用尾插法初始化链表,并建立n个基本数据
	//因为是尾插法，要求输入的数据应该是正序从表头输入到表尾
	l=(linklist)malloc(sizeof(lnode));//申请一个头结点
	//malloc函数格式是(申请空间类型*)malloc(申请空间大小)，linklist等同于*lnode所以这里前面直接使用linklist即可
	if(!l) return error;	//如果申请失败，返回error信号
	l->next=NULL;	//设置头结点的指针为空，现在的链表还是空链表
	linklist p=l;
	for(int i=1;i<=n;i++){
		linklist q=(linklist)malloc(sizeof(lnode));
		q->next=NULL;
		cin>>q->data;	//C++的输入流语句
		p->next=q;		//尾插法将新的结点永远接在表尾
		p=q;	//因为表尾插入了新元素，所以新元素则为新的表尾
	}
	return TRUE;
}
status destroylist_l(linklist &l){//销毁链表释放空间
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	linklist p,q;
	q=l;
	for(p=l->next;p->next!=NULL;p=p->next){//链表利用只有最后一个结点的指针是空指针的特点，销毁除最后一个结点的每一个结点
		free(q);
		q=p;
	}
	free(p);//消除最后一个结点
	return TRUE;
}
status clearlist_l(linklist &l){//清空链表
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	linklist p,q;
	q=l->next;
	for(p=q->next;p->next!=NULL;p=p->next){//链表利用只有最后一个结点的指针是空指针的特点，销毁除最后一个结点和头结点以外的每一个结点
		free(q);
		q=p;
	}
	free(p);//消除最后一个结点
	l->next=NULL;	//这里一定要记得清理链表完毕后，要将头指针重新置空，我在这里卡了很久没发现
	return TRUE;
}
status listempty_l(linklist l){
	//如果链表为空表就返回TRUE否则返回FALSE
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	if(l->next==NULL){
		return TRUE;
	}
	return FALSE;
}
int listlength_l(linklist l){//求链表长度
	linklist q;
	int i=0;
	for(q=l->next;q;q=q->next){
		i++;
	}
	return i;
}
status get_elem_l(linklist &l,int i,elemtype &e){
	//在链表l中取第i个元素赋值给e并返回OK
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	linklist p=l;
	for(int j=1;j<=i&&p;j++){
		p=p->next;		
	}
	if(!p||i<1){
		return error;//如果链表长度不够,或者i<1就报错
	}
	e=p->data;
	return TRUE;
}
int locate_elem_l(linklist l,elemtype e){
	//返回链表l中第一个与e相同的的数据元素的位置，如果不存在返回0
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	int i=0;
	linklist q;
	for(q=l->next;q;q=q->next){
		i++;
		if(e==q->data)
			break;
	}
	if(!q)	return error;	//如果表中不存在e元素，就报错
	return i;
}
status prior_elem_l(linklist l,elemtype cur_e,elemtype &pre_e){//求前驱函数，在线性表l返回cur_e的前驱并赋值给pre_e
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	linklist p,q;
	p=l->next;
	for(q=p->next;q;q=q->next){
		if(cur_e==q->data)
			break;
		p=q;
	}
	if(!q)	return error;	//如果表中不存在e元素或者e数据元素是首个数据没有前驱，就报错
	pre_e=p->data;
	return TRUE;
}
status next_elem_l(linklist l,elemtype cur_e,elemtype &next_e){
	//求后继函数，在链表l返回cur_e的后一个数据元素并赋值给next_e
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	linklist q;
	for(q=l->next;q;q=q->next){
		if(cur_e==q->data)
			break;
	}
	if(!q||q->next==NULL)	return error;	//如果表中不存在e元素或者e数据元素是最后一个元素没有后驱，就报错
	next_e=q->next->data;
	return TRUE;
}
status listinsert_l(linklist &l,int i,elemtype e){//在带头结点的链表l中的第i个位置之前插入新的数据元素e
	if(!l||i<1){
		return error;//如果表没有初始化或者i小于1就报错，返回error信号
	}
	linklist q=l;
	int j;
	for(j=0;q&&j<i-1;j++){
		q=q->next;
	}//找到第i-1个
	if(i>j+1){
		return error;
	}//如果i比链表长度+1还长
	linklist p=(linklist)malloc(sizeof(lnode));	//申请一个结点
	p->data=e;	//赋值
	p->next=q->next;
	q->next=p;
	return TRUE;
}
status listdelete_l(linklist &l,int i,elemtype &e){
	//删除链表l第i个数据元素，并用e返回其值，l的长度减一
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	linklist p,q=l;
	for(int j=1;q&&j<=i;j++){
		p=q;
		q=q->next;
	}
	if(!q||i<1){
		return error;
	}//如果i比链表长度+1还长或者小于1就报错
	e=q->data;
	p->next=q->next;
	free(q);
	return TRUE;
}
status list_traverse_l(linklist l){
	//遍历线性表，将线性表中的所有数据元素查看一遍
	linklist q;
	for(q=l->next;q;q=q->next){
		cout<<q->data<<" ";
	}
	cout<<endl;
	return TRUE;
}

int main(){
	linklist l;
	int sign;
	elemtype e;
	sign=createlist_l_tail(l,3);
	if(sign==-1){
		printf("This (createlist_l) was wrong!\n");	//错误信号处理;
	}

	//...
	list_traverse_l(l);
	sign=destroylist_l(l);
	if(sign==-1){
		printf("This (destroylist_l) was wrong!\n");	//错误信号处理;
	}
	return 0;
}

链表的重点应该是尾插和头插法，所以要着重注意头插法和尾插法的原理，和区别。

线性链表的扩展

• 扩展：利用头插法实现链表的转置，比如要求将链表L={27,16,10}转置，请你设计算法实现：

void list_reversal_l(linklist &l){//用头插法将链表l翻转
	linklist t,q,p;
	t=q=l->next;	//因为转置后第一个结点会变成最后一个结点，所以这里用t记录一下结点
	for(;q;){
		p=q->next;	//因为后面q的next指针就被更改了，但是next的结点下一轮循环还需要使用，所以这里应该提前记忆一下next的信息
		q->next=l->next;	//头插法，将结点插到表头
		l->next=q;
		q=p;	//进入下一个结点进行循环
	}
	t->next=NULL;	//最后一个结点next置空
	return;
}

2.4 顺序表和链表在复杂度上的区别

插入和删除

顺序表：

• 最好的情况：新元素插表尾，不需要移动数据，时间复杂度为$O(1)$;
• 最坏的情况：新元素插表头，移动原有的n个所有数据，时间复杂度$O(n)$;
• 平均情况：假设新元素插入到任何一个位置的概率相同，则平均移动$\frac{n}{2}$个元素，所以平均时间复杂度$O(\frac{n}{2})$，即$O(n)$;

链表：

• 最好的情况：新元素插表头，指针能不用移动直接插入，时间复杂度为$O(1)$;
• 最坏的情况：新元素插表尾，指针移动经过到n个结点后才可插入，时间复杂度$O(n)$;
• 平均情况：假设新元素插入到任何一个位置的概率相同，则平均查找$\frac{n}{2}$个元素，所以平均时间复杂度$O(\frac{n}{2})$，即$O(n)$;

删除同理。

查找

顺序表：

• 按位查找：最好、最坏、平均时间都是$O(1)$
• 按值查找：最好的情况目标元素在表头，时间复杂度为$O(1)$，最坏的情况目标元素在表尾，时间复杂度$O(n)$；平均情况假设目标元素在任何一个位置的概率相同，则平均查找$\frac{n}{2}$个元素，所以平均时间复杂度$O(\frac{n}{2})$，即$O(n)$;

链表：

• 无论是按位查找还是按值查找，时间复杂度都是$O(n)$;

2.5 双链表

双链表的含义

双链表，可进可退，比单链表多消耗一点存储空间来储存前驱的地址。

双链表的部分实现

这里只实现一部分函数，因为大多数函数操作是和单链表相差不大的，重复写我觉得没有多大的意义。

#include 
using namespace std;

#define error -1	//因为C语言中没有true和false关键字，虽然C++里有但是这里还是额外定义一下
#define FALSE 0
#define TRUE 1
typedef int elemtype;	//定义数据元素类型，这样做的好处是想要修改类型时只需修改这句话就可以了
typedef int status;	//因为C语言编译器中一般不存在bool,所以这里的定义相当于C++的bool类型，代表函数返回的状态

struct dulnode{
	elemtype data;
	struct dulnode *prior;//前驱指针
	struct dulnode *next;//后驱指针
};
typedef dulnode *dulinklist;

status init_dulinklist(dulinklist &l){//初始化带头结点双向链表指针
	l=(dulinklist )malloc(sizeof(dulnode));	//创建头结点
	if(!l)return error;//如果创建失败，返回错误信号
	l->next=NULL;
	l->prior=NULL;
	return TRUE;
}
status listinsert_dul(dulinklist &l,int i,elemtype e){//在带头结点的双向链表l中的第i个位置之前插入新的数据元素e
	if(!l||i<1){
		return error;//如果表没有初始化或者i小于1就报错，返回error信号
	}
	dulinklist q=l;
	int j;
	for(j=0;q&&j<i-1;j++){
		q=q->next;
	}//找到第i-1个
	if(i>j+1){
		return error;
	}//如果i比链表长度+1还长
	dulinklist p=(dulinklist)malloc(sizeof(dulnode));	//申请一个结点
	p->data=e;	//赋值
	p->next=q->next;
	if(q->next)q->next->prior=p;	//避免q为最后一个结点，当q为最后一个结点的时候没有后驱，指针为空
	q->next=p;
	p->prior=q;
	return TRUE;
}
status listdelete_dul(dulinklist &l,int i,elemtype &e){//删除在带头结点的双向链表l中的第i个位置的数据元素，并将删除的值赋值回e
	if(!l||i<1){
		return error;//如果表没有初始化，返回error信号
	}
	dulinklist q=l;
	int j;
	for(j=0;q&&j<i;j++){
		q=q->next;
	}//找到第i个
	if(!q){
		return error;
	}//如果i比链表长度还长或者小于1就报错
	q->prior->next=q->next;
	if(q->next)q->next->prior=q->prior;
	e=q->data;
	free(q);
	return TRUE;
}
status destroylist_dul(dulinklist &l){//销毁链表释放空间
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	dulinklist p,q;
	q=l;
	for(p=l->next;p->next!=NULL;p=p->next){//链表利用只有最后一个结点的指针是空指针的特点，销毁除最后一个结点的每一个结点
		free(q);
		q=p;
	}
	free(p);//消除最后一个结点
	return TRUE;
}
status list_traverse_dul(dulinklist l){
	//遍历线性表，将线性表中的所有数据元素查看一遍
	dulinklist q;
	for(q=l->next;q;q=q->next){
		cout<<q->data<<" ";
	}
	cout<<endl;
	return TRUE;
}
int main(){
	dulinklist l;
	int sign;
	elemtype e;
	sign=init_dulinklist(l);
	if(sign==-1){
		printf("This (createlist_l) was wrong!\n");	//错误信号处理;
	}
	//...
	list_traverse_dul(l);
	sign=destroylist_dul(l);
	if(sign==-1){
		printf("This (destroylist_l) was wrong!\n");	//错误信号处理;
	}
	return 0;
}

2.6 循环链表

循环链表的含义

循环链表分为循环单链表和循环双链表两种：
循环单链表：与单链表唯一的差别就是，表中的最后一个结点的指针不是NULL，而改为只想头结点，从而整个链表形成一个环。如下图：

note:很多时候对链表的操作都是在头部和尾部
指针L的位置如果在头结点：找到尾部的时间复杂度$O(n)$
指针L的位置如果在尾结点：找到头结点的时间复杂度$O(1)$，而且尾部的时间复杂度也是$O(1)$，只是在插入和删除时可能需要多修改一个L的位置。

循环双链表：与双链表的差别就是，表头结点的prior指向表尾，表尾结点的next指向头结点。如下图：

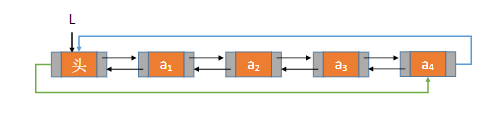
循环双链表的部分实现

#include 
using namespace std;

#define error -1	//因为C语言中没有true和false关键字，虽然C++里有但是这里还是额外定义一下
#define FALSE 0
#define TRUE 1
typedef int elemtype;	//定义数据元素类型，这样做的好处是想要修改类型时只需修改这句话就可以了
typedef int status;	//因为C语言编译器中一般不存在bool,所以这里的定义相当于C++的bool类型，代表函数返回的状态

struct dulnode{
	elemtype data;
	struct dulnode *prior;//前驱指针
	struct dulnode *next;//后驱指针
};
typedef dulnode *dulinklist;

status init_dulinklist(dulinklist &l){//初始化带头结点双向链表指针
	l=(dulinklist )malloc(sizeof(dulnode));	//创建头结点
	if(!l)return error;//如果创建失败，返回错误信号
	l->next=l;//循环链表尾结点next指向表头
	l->prior=l;//链表头结点prior指向表尾
	return TRUE;
}
status listinsert_dul(dulinklist &l,int i,elemtype e){//在带头结点的双向链表l中的第i个位置之前插入新的数据元素e
	if(!l||i<1){
		return error;//如果表没有初始化或者i小于1就报错，返回error信号
	}
	dulinklist q=l;
	int j;
	for(j=0;q->next!=l&&j<i-1;j++){
		q=q->next;
	}//找到第i-1个
	if(i>j+1){
		return error;
	}//如果i比链表长度+1还长
	dulinklist p=(dulinklist)malloc(sizeof(dulnode));	//申请一个结点
	p->data=e;	//赋值
	p->next=q->next;
	q->next->prior=p;	//这里和单向双链表不一样注意区分
	q->next=p;
	p->prior=q;
	return TRUE;
}
status listdelete_dul(dulinklist &l,int i,elemtype &e){//删除在带头结点的双向链表l中的第i个位置的数据元素，并将删除的值赋值回e
	if(!l||i<1){
		return error;//如果表没有初始化，返回error信号
	}
	dulinklist q=l;
	int j;
	for(j=0;q->next!=l&&j<i;j++){
		q=q->next;
	}//找到第i个
	if(i>j){
		return error;
	}//如果i比链表长度还长报错
	q->prior->next=q->next;
	q->next->prior=q->prior;//这里和单向双链表不一样注意区分
	e=q->data;
	free(q);
	return TRUE;
}
status destroylist_dul(dulinklist &l){//销毁链表释放空间
	if(!l){
		return error;//如果表没有初始化，返回error信号
	}
	dulinklist p,q;
	q=l;
	for(p=l->next;p->next!=l;p=p->next){//链表利用只有最后一个结点的指针是空指针的特点，销毁除最后一个结点的每一个结点
		free(q);
		q=p;
	}
	free(p);//消除最后一个结点
	return TRUE;
}
status list_traverse_dul(dulinklist l){
	//遍历线性表，将线性表中的所有数据元素查看一遍
	dulinklist q;
	for(q=l->next;;q=q->next){
		cout<<q->data<<" ";
		if(q->next==l)break;
	}
	cout<<endl;
	return TRUE;
}
status list_reverse_traverse_dul(dulinklist l){
	//遍历线性表，将线性表中的所有数据元素反向查看一遍
	dulinklist q;
	for(q=l->prior;;q=q->prior){
		cout<<q->data<<" ";
		if(q->prior==l)break;
	}
	cout<<endl;
	return TRUE;
}
int main(){
	dulinklist l;
	int sign;
	elemtype e;
	sign=init_dulinklist(l);
	if(sign==-1){
		printf("This (createlist_l) was wrong!\n");	//错误信号处理;
	}
	//...
	sign=destroylist_dul(l);

	if(sign==-1){
		printf("This (destroylist_l) was wrong!\n");	//错误信号处理;
	}
	return 0;
}

2.7 静态链表

静态链表的定义

静态链表：分配一段连续的内存空间，各个结点集中安置。

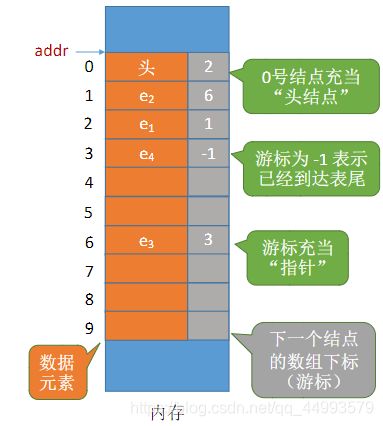
静态链表如上图所示，接下来用一个单链表作类比
静态链表内存中的addr指针相当于单链表中的L，游标相当于单链表中的next指针，与单链表不同的是，静态链表由数组存放，而单链表是一个一个分开的结点存放构成。
也就是说单链表的实现需要依靠指针申请空间操作的，但是有些低级语言是不存在这种操作的，但是又想在这种低级语言的环境下使用单链表的特性和功能，这时候静态链表就由此而生了。

静态链表的部分实现

静态链表的实现的难点在于：需要自己实现在实现单链表时所用的malloc函数和free函数。
这时候想要实现这两个函数的功能就需要引出备用链表的概念了。
备用链表的作用是回收数组中未使用或之前使用过（目前未使用）的存储空间，留待后期使用。

也就是说：静态链表使用数组申请的物理空间中，存有两个链表，一条连接数据，另一条连接数组中未使用的空间。

在这里注意：游标为0时，链表达到链尾。且备用链表的头指针为space[0].cur+
，而如果有数据则数据链表的头指针为space[MAXSIZE-1].cur。

#include 
using namespace std;

#define error -1	//因为C语言中没有true和false关键字，虽然C++里有但是这里还是额外定义一下
#define FALSE 0
#define TRUE 1
#define MAXSIZE 1000
typedef int elemtype;	//定义数据元素类型，这样做的好处是想要修改类型时只需修改这句话就可以了
typedef int status;	//因为C语言编译器中一般不存在bool,所以这里的定义相当于C++的bool类型，代表函数返回的状态

typedef struct{
	elemtype data;
	int cur;
}component,slinklist[MAXSIZE];
	
status initspace_sl(slinklist &space){
	//初始化静态链表，这时候静态链表还没有存放数据，所以其实是初始化备用链表而已
	//将一维数组space空闲的存储空间全部链成一个链表，sqace[0].cur为头指针
	for(int i=0;i<MAXSIZE-1;i++){
		space[i].cur=i+1;
	}
	space[MAXSIZE-1].cur=0;
	return TRUE;
}
int malloc_sl(slinklist &space){
	//若备用空间链表非空，则返回分配的结点下标，否则返回错误信号0
	int i=space[0].cur;
	if(space[0].cur)//如果备用链表没到链尾，就表示还有空间可以分配
		space[0].cur=space[i].cur;//空间被分配出去了，备用链表需要更新一下
	return i;
}
status free_sl(slinklist &space,int k){
	//将下标为k的结点回收到备用链表
	space[k].cur=space[0].cur;
	space[0].cur=k;
	return true;
}
status listinsert_sl(slinklist &space,int i,elemtype e){
	//在静态链表中的第i个位置之前插入新的数据元素e
	if(!space||i<1)
		return error;
	int j;
	int t=space[MAXSIZE-1].cur;//指向头指针
	for(j=1;j<=i-1;j++){//定位到第i-1个元素的位置
		if(!t)	break;
		t=space[t].cur;
	}
	if(i>j+1){
		return error;//如果i比链表长度+1还长则返回错误信号
	}
	int c=malloc_sl(space);
	space[c].data=e;
	space[c].cur=space[t].cur;
	space[t].cur=c;
	return TRUE;
}
status list_traverse_sl(slinklist sl){
	//遍历线性表，将线性表中的所有数据元素查看一遍
	int t=sl[MAXSIZE-1]
}
int main(){
	slinklist sl;
	initspace_sl(sl);

	return 0;
}