数据结构和算法：归并排序（合并排序）详解

归并排序(Merge Sort)是用分治策略（分治法）实现对n个元素进行排序的一种高速的、稳定的排序算法。

在介绍归并排序之前，我们首先简单的认识一下分治法

分治法

基本思想：
将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且原问题相同。递归地解这些子问题，然后将各子问题的解合并得到原问题的解。
精髓：
分——将问题分解为规模更小的子问题。
治——将这些规模更小的子问题逐个击破。
合——将已解决的子问题合并，最终得到原问题的解。

在简单的了解过分治法之后，我们便开始介绍本文的“主角”——归并排序了。在正式介绍之前，再补充说明一下：归并排序是分治法的一个典型应用和完美体现，它是一种平衡的、简单的二分分治策略。

归并排序

基本思想：
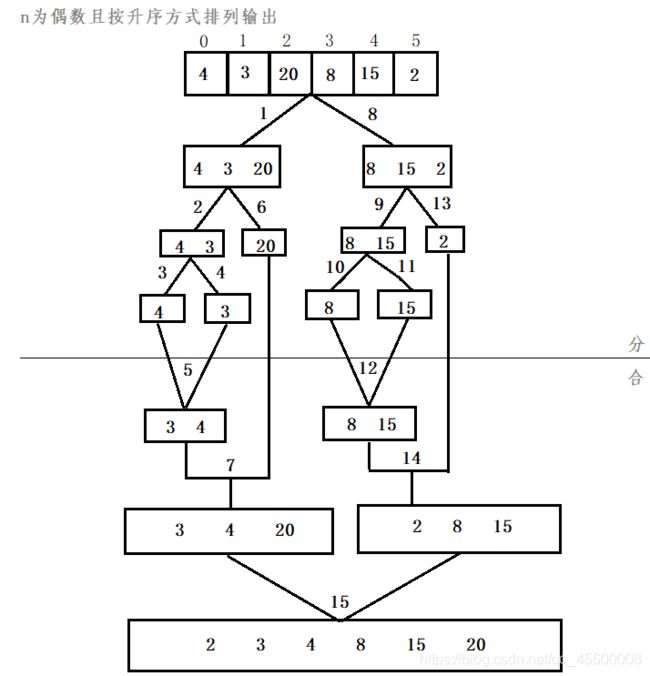
将原始数组A[0:n-1]中的元素分成两个大小大致相同的子数组：A[0:n/2]和A[n/2+1:n-1]，分别对这两个子数组单独排序，然后将已排序的两个数组归并成一个含有n个元素的有序数组。（不断地进行二分，直至待排序数组中只剩下一个元素为止，然后不断合并两个排好序的数组段）
稳定性：
归并排序包括不相邻元素之间的比较，但并不会直接交换。在合并两个已排序数组时，如果遇到了相同元素，只要保证前半部分数组优先于后半部分数组，相同元素的顺序就不会颠倒。
复杂度：
时间复杂度：
归并排序算法的时间复杂度为O(nlogn)。（logn即为log₂n）
解析如下：
当n=1时：T(n)=O(1)
当n>1时：T(n)=2T(n/2)+O(n)
其中，O(1)代表仅仅是计算出子序列的中间位置需要的常数时间。
2T(n/2)代表递归求解两个规模为n/2的子问题所需的时间。
O(n)代表合并算法可以在O(n)时间内完成。（因合并处理中，由于两个待处理的序列（局部数组）都已经完成了排序，因此可以在O(n₁+n₂)->O(n)时间内完成，n₁指前半部分序列的长度，n₂指后半部分序列的长度）
解T(n)=2T(n/2)+O(n)由递推求解得：
T(n)=2^xT(n/2^x)+xO(n)
当递推最终的规模为1时，n/2^x=1，那么x=logn
则T(n)=nT(1)+logn*O(n)=n+lognO(n)=O(nlogn)
空间复杂度：
程序中变量占用了一些辅助空间，这些辅助空间都是常数阶，每合并一次会分配一个适当大小的缓冲区，且在退出时释放。最多分配大小为n，所以空间复杂度为O(n)。
递归调用占用的栈空间是递归树的深度logn

在介绍完归并排序的基本思想、稳定性和复杂度之后，我们在看代码实现之前先看下图解了解一下。

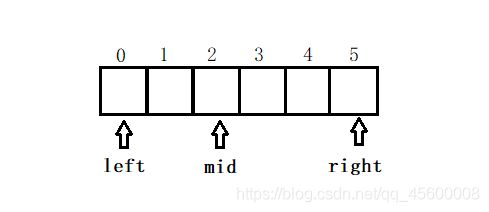
归并排序中遇到的下标（标记）
left代表序列在数组中的下界
mid代表下界和上界的中间位置（mid=(left+right)/2）
right代表序列在数组中的上界

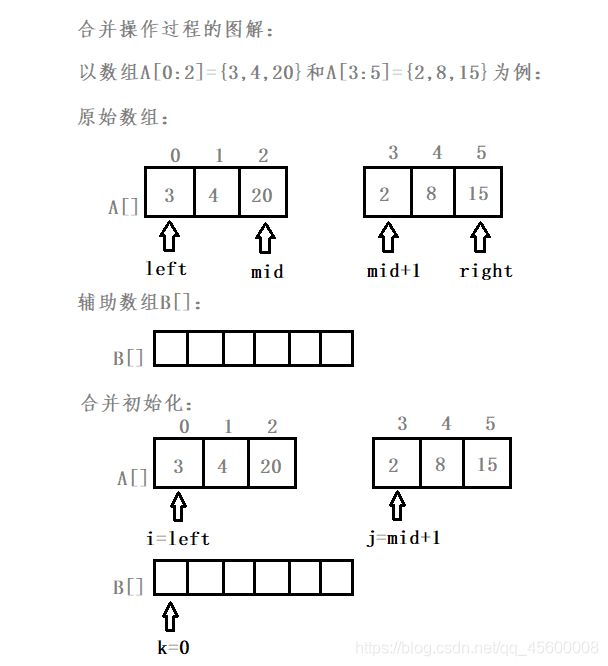
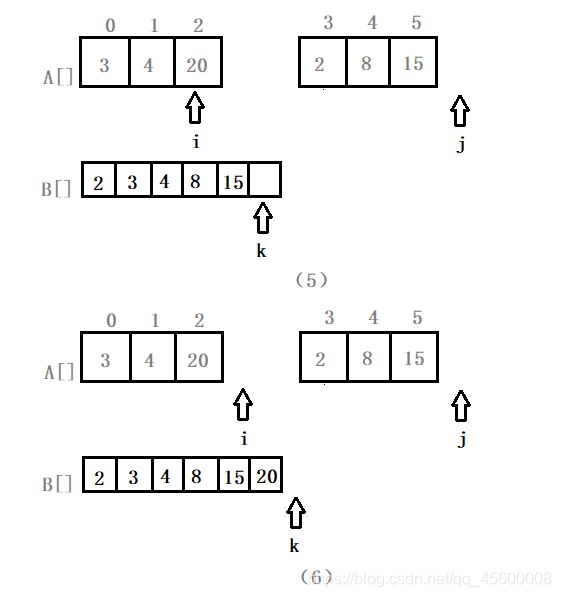
接下来我们举个例子来看一下当n为偶数的时候归并排序的过程以及合并操作过程的图解

在看过图解之后，接下来就看下对应的代码实现：

辅助合并函数Merge(A,left,mid,right)，该函数将排好序列的两个子序列A[left:mid]和A[mid+1:right]进行合并。（整个算法的基础）

void Merge(int A[], int left, int mid, int right)             //合并操作的代码实现
{
	int *B = new int[right - left + 1];                       //申请一个辅助数组B[]，与传递过来的序列数组等长
	//图中的三个辅助标记（工作指针）
	int i = left;                                             //指向待排序子序列数组A[left:mid]中当前待比较的元素
	int j = mid + 1;                                          //指向待排序子序列数组A[mid+1:right]中当前待比较的元素
	int k = 0;                                                //k指向辅助数组B[]中待放置元素的位置

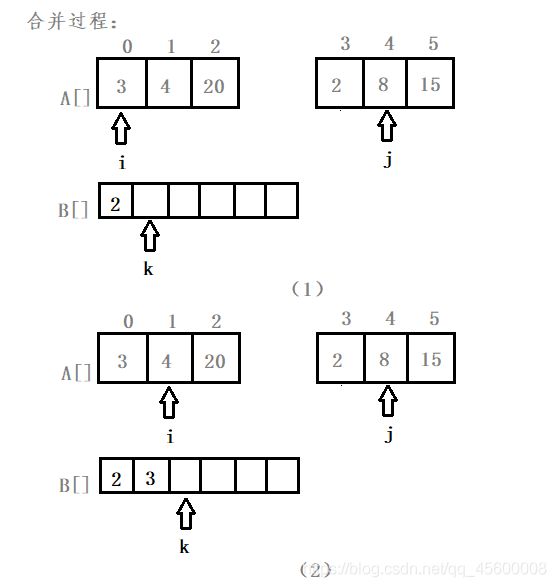
	while (i <= mid && j <= right)                             //当i和j都指向未超过数组范围的时候
	{                                                          //从小到大排序，将A[i]和A[j]中的较小元素放入B[]中
		if (A[i] <= A[j])                                      //当前半部分数组A[left:mid]的值不大于后半部分数组A[mid+1:right]的值时，将前半部分数组辅助标记对应的值存入辅助数组中（具有稳定性）
			B[k++] = A[i++];                                   //存入辅助数组B[]中，且与之对应的辅助标记后移
		else                                                   //否则将后半部分辅助标记对应的值存入B[]中
			B[k++] = A[j++];                                   //存入辅助数组且与之对应的辅助标记后移
	}

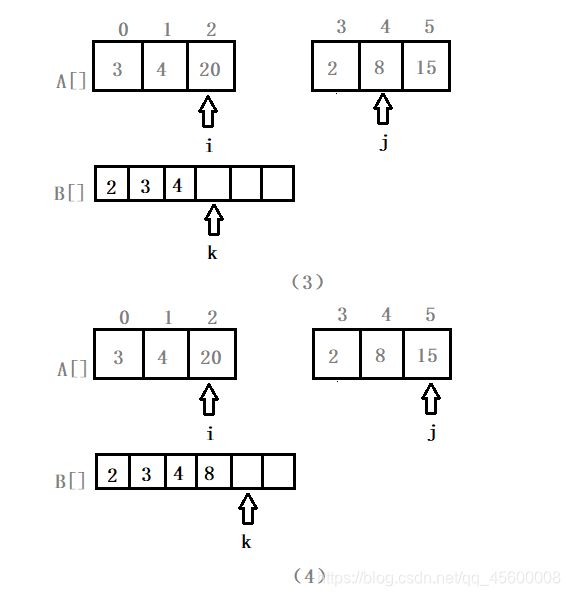
	while (i <= mid)                                           //对序列A[left:mid]剩余的部分依次进行处理，与图中的（5）对应
		B[k++] = A[i++];                                       //将辅助标记对应的值存入辅助数组中且辅助标记后移

	while (j <= right)                                         //对序列A[mid+1:right]剩余的部分依次进行处理
		B[k++] = A[j++];                                       //将辅助标记对应的值存入辅助数组中且辅助标记后移  

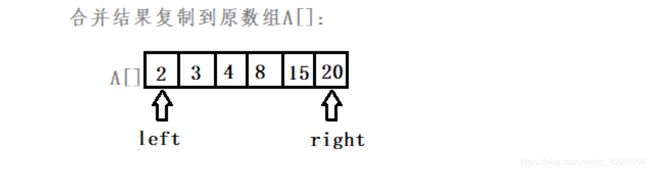
	for (i = left, k = 0; i <= right; i++)                     //将合并后的序列复制到原来的A[]序列
		A[i] = B[k++];

	delete[] B;                                                //释放动态创建的辅助数组空间
}

递归形式的归并排序函数MergeSort(A,left,right)
1、将给定的包含n个元素的局部数组“分割”成两个局部数组。
2、对两个局部数组分别执行归并排序。
3、通过合并函数Merge(A,left,mid,right)将两个已排序完毕的局部数组“整合”成一个数组。

//递归形式的归并排序算法
void MergeSort(int A[], int left, int right)                   //归并排序
{
	if (left < right)                                          //当数组内的元素数大于1时进行二分操作，只有一个元素的时候，不作任何处理直接结束
	{
		int mid;
		mid = (left + right) / 2;                              //计算中间位置
		MergeSort(A, left, mid);                               //对数组A[left:mid]中的元素进行归并排序
		MergeSort(A, mid + 1, right);                          //对数组A[mid+1:right]中的元素进行归并排序
		Merge(A, left, mid, right);                            //进行合并操作
	}
}

在了解完代码实现后，看下归并排序的代码实现的执行顺序（与图解的联系）

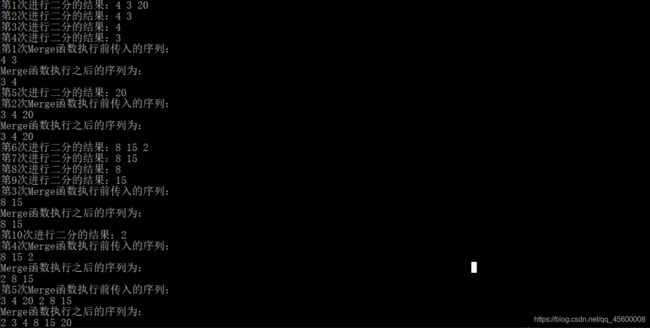
归并排序的改进

1、在数组长度比较短的情况下不进行递归，而选择其他排序方案：如插入排序。
2、归并过程中，可以用记录数组下标的方式代替申请新内存空间，从而避免A和辅助数组间的频繁数据移动。
3、从分支策略的机制入手，容易消除算法中的递归：
先将数组A中相邻元素两两配对。用合并算法将他们排序，构成n/2组长度为2的排好序的子数组段，再将他们排序成长度为4的排好序的子数组段。如此继续下去，直至整个数组排好序。

//消去递归后的合并排序算法可描述如下：
void Merge(ElemType C[], ElemType D[], int left, int mid, int right)                               //合并C[left:mid]和C[mid+1:right]到D[left:right]
{
	int i = left;
	int j = mid + 1;
	int k = left;

	while (i <= left && j <= right)
		if (C[i] <= C[j])
			D[k++] = C[i++];
		else
			D[k++] = C[j++];

	while (i <= mid)
		D[k++] = C[i++];

	while (j <= right)
		D[k++] = C[j++];
}

void MergePass(ElemType X[], ElemType Y[], int s, int n)       //函数MergePass()用于合并排好序的相邻数组段，具体的合并算法由Merge()函数来实现
{                                                              //合并大小为s的相邻子数组
	int i = 0;         

	while (i <= n - 2 * s)
	{
		Merge(X, Y, i, i + s - 1, i + 2 * s - 1);              //合并大小为s的相邻2段子数组
		i = i + 2 * s;                                         //标记后移
	}

	if (i + s < n)                                              //剩下的元素个数小于2s
		Merge(X, Y, i, i + s - 1, n - 1);
	else
		for (int j = i; j <= n - 1; j++)
			Y[j] = X[j];
}

void MergeSort(ElemType A[], int n)
{
	ElemType *B = new ElemType[n];                          //动态申请一个辅助数组
	int s = 1;
	while (s < n)                                           //当数组A[]中的元素个数大于1时
	{
		MergePass(A, B, s, n);                              //合并到数组B
		s += s;
		MergePass(B, A, s, n);                              //合并到数组A
		s += s;
	}
}

例题

题目描述

利用归并排序法将包含n个整数的数列S按升序排序

输入

输入有两行：第一行输入一个正整数n，第二行输入n个整数

输出

输出排序完毕的数列S，相邻的元素之间空格隔开

程序代码如下

#include
#include
#define ElemType_I int

using namespace std;

void Merge(ElemType_I A[], ElemType_I left, ElemType_I mid, ElemType_I right)             //合并
{
	ElemType_I *B = new ElemType_I[right - left + 1];                                     //申请辅助数组
	ElemType_I i = left;
	ElemType_I j = mid + 1;
	ElemType_I k = 0;

	while (i <= mid && j <= right)
		if (A[i] <= A[j])
			B[k++] = A[i++];
		else
			B[k++] = A[j++];

	while (i <= mid)
		B[k++] = A[i++];

	while (j <= right)
		B[k++] = A[j++];

	for (i = left, k = 0; i <= right; i++)
		A[i] = B[k++];

	delete[] B;
}

void MergeSort(ElemType_I A[], ElemType_I left, ElemType_I right)                             //递归形式的归并排序
{
	if (left < right)
	{
		ElemType_I mid;
		mid = (left + right) / 2;
		MergeSort(A, left, mid);
		MergeSort(A, mid + 1, right);
		Merge(A, left, mid, right);
	}
}

int main()
{
	ElemType_I n;
	cin >> n;
	ElemType_I *A = new ElemType_I[n];
	for (int i = 0; i < n; i++)
		cin >> A[i];

	MergeSort(A, 0, n - 1);                                          //调用归并排序              

	for (int i = 0; i < n; i++)
		cout << A[i] << " ";

	cout << endl;
	//system("pause");                                                        //输出暂停，头文件

	return 0;
}

程序运行结果如下

[注释1]：当n为奇数时的图解以及稳定性的图解与上述类似，因此就不再进行描述了。归并排序也可以将数组分成A[left:mid]和A[mid:right]，其中left指局部数组的开头元素，right指局部数组末尾+1的元素，A[left:mid]包括left到mid（不包括mid），A[mid:right]包括mid到right（不包括right），但其代码实现和图解需要部分修改。
[注释2]：基于关键字比较的排序算法的平均时间复杂度的下界为O(nlogn)