知识表示学习【知识图谱专栏】

一、知识图谱

知识图谱是将现实世界的具象事物与抽象概念表示为实体，将实体间的联系表示为关系，并最终以（头实体、关系、尾实体）三元组为基本元素结构来表示知识。

比如：

• （淘宝，从属于，阿里巴巴）

• （支付宝，从属于，阿里巴巴）

1、符号定义：

2、三元组表示的缺陷：

• 计算效率低下。知识图谱的三元组符号表示需要图算法进行计算。这些图算法计算复杂度较高，在大规模知识图谱上难以快速运行，难以扩展至其他情况。
• 数据稀疏性强。大规模知识图谱中的实体与关系存在长尾分布，有很多实体只存在着极少数的关系与之相连。对这些稀疏的实体和关系，往往很难有效理解与推理。

故需要对三元组表示的缺陷，思考其他表示方法，弥补这些缺陷。

二、知识表示学习

知识表示学习基于分布式表示的思想，将实体（或关系）的语义信息映射到低维、稠密、实值的向量空间（联想词向量的One-hot表示与word2vec词向量表示），使得语义相似的两个对象之间的距离也相近。用粗体的符号h，t，r表示头尾实体与关系对应的表示向量。

比如将：

• （淘宝，从属于，阿里巴巴）

• （支付宝，从属于，阿里巴巴）

映射到一个向量空间，用向量表示每个三元组信息。实体对应空间的一个点，语义相近的两个实体，在向量空间中，它们的向量表示应该比较相近。

如 淘宝 和 支付宝，这两个实体应该比较相近的，认为这两个向量表示是不同的，他们之间有一定的区分。

1、分布式表示的特点：

• 分布式表示学习到的是低维向量。使得实体与关系之间的语义联系能够在低维空间中得以高速计算，提升计算效率。

• 传统独热表示基于所有对象的相互独⽴假设，所有向量之间两两正交，丢失了⼤量对象之间的相似及关联信息。而分布式表示则能通过稠密低维向量之间的相似度计算表达对象之间的关系，较好地缓解数据稀疏带来的问题。

• 分布式表示能够将多源异质信息映射到同一语义空间中，建立多源跨模态的信息交互，且分布式表示也能更便捷地融入深度学习的模型框架中。（可以结合语音、图像、文本信息，实现跨模态）

2、三元组和词向量分布式表示

词向量表示：

• 离散表示（one-hot representation）

  把每个词表示为一个长向量。这个向量的维度是词表大小，向量中只有一个维度的值为1，其余维度为0，这个维度就代表了当前的词。

  面临着数据稀疏性和维度灾难的问题。优势在于高维空间中，很多应用任务线性可分。

• 分布式表示（distribution representation）

  将词转化成一种分布式表示，又称词向量（Word embedding）。将词表示成一个定长的连续的稠密向量。

  分布式表示优点：

  (1) 词之间存在相似关系，存在“距离”概念，这对很多自然语言处理的任务非常有帮助。

  (2) 词向量能够包含更多信息，并且每一维都有特定的含义。

可发现，词向量和三元组的知识表示核心思想是十分一致的，都是解决数据稀疏和维度灾难的问题而提出的向量化的方法。三元组和词向量结合，也有相应的应用，例如：word2vec + transE 知识表示模型

word2vec + transE 知识表示模型

• 将文本方法 (word2vec) 和知识库方法 (transE) 相融合作知识表示，即将外部知识库信息（三元组）加入word2vec语言模型，作为正则项指导词向量的学习，将得到的词向量用于分类任务，提升模型效果。

三、知识表示经典模型

1、TransE模型

TransE模型

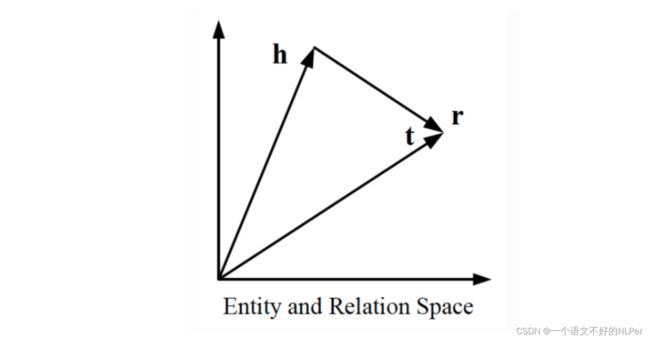
应用词向量空间存在平移不变的特性，将知识库中的关系看作实体间的某种平移向量。对于每个事实三元组(h,r,t)，TransE模型将实体和关系表示为同一空间中，把关系向量r看作为头实体向量h和尾实体向量t之间的平移即h+r≈t。

比如：对于给定的2个事实

• (淘宝，从属, 阿里巴巴)
• (天美, 从属, 腾讯)

除了可以得到：淘宝 + 从属≈阿里巴巴 和 天美 + 从属≈腾讯，还可以通过平移不变性得到：腾讯 - 天美 ≈ 阿里巴巴 –淘宝，即得到两个事实相同的关系的向量表示。

我们也可以将r,看作从h到t，的翻译，因此TransE也被称为翻译模型。

知识库中的实体关系类型可分为 一对一 、一对多 、 多对一 、多对多4 种类型，而复杂关系主要指的是 一对多 、 多对一 、多对多的 3 种关系类型。

$$具体地,对于给定的三元组(h,r,t),TransE模型将关系r看作从头实体h到尾实体的平移向量。$$

$$基于以上平移假设,平移模型得到一个三元组的实体与关系向量\mathbf{h},\mathbf{t},\mathbf{r}\in {\mathbb{R}}^d之间存在\mathbf{h}+\mathbf{r}\approx \mathbf{t}的关系。$$

$$形式化地,TransE模型对三元组(h,r,t)定义如下评分函数：$$

$$E(h,r,t)=\Vert \mathbf{h}+\mathbf{r}-\mathbf{t}{\Vert }_{L_1/L_2}，评分函数应该是在0附近的量，越接近于0，则效果越好。$$

$$实际中,TransE模型使用最大间隔方法,定义目标函数$$

$$\mathcal{L}=\sum _{(h,r,t)\in \mathcal{T}}\sum _{\left(h^{\prime },r,t^{\prime }\right)\in {\mathcal{T}}^{\prime }}\max \left(\gamma +E(h,r,t)-E\left(h^{\prime },r,t^{\prime }\right),0\right)$$

$$其中,\mathcal{T}为正例三元组集合,{\mathcal{T}}^{\prime }=\left\{\left(h^{\prime },r,t\right)\mid h^{\prime }\in \mathcal{E}\right\}\cup \left\{\left(h,r,t^{\prime }\right)\mid t^{\prime }\in \mathcal{E}\right\}为负例三元组集合$$

$$\gamma >0为正负例三元组得分的间隔距离。TransE模型通过最大化正负例三元组之间的得分差来优化知识表示。$$

• 减去负例三元组集合的评分函数是因为：无关实体间的差异性越大越好，相关实体间的差异越接近越好，由一个约等于0的值减去一个正值，则前面的整体是一个负值，通过取max，如果前面部分是负值，最终取到的是0。
• 为什么要使用max？：当前面的部分结果为负值时，无关样本差异越大，是我们理想的结果，这对模型而言没有损失，故通过max将目标函数得分进行修正为0，若前面部分结果为正时，则取前面的结果（此时是有损失的）。
• γ的意义：如果无关实体间差异性较小，则无法区分损失是来源于正例样本的约等于的影响，还是负例样本之间的差异，故引入超参数γ（γ＞0），控制无关样本的差异程度，相当于一个阈值，超出一定范围，才可认为没有损失。

问题：

虽然TransE模型的参数较少，计算的复杂度显著降低，并且在大规模稀疏知识库上也同样具有较好的性能与可扩展性。但是TransE 模型不能用在处理复杂关系上，比如对于一个集团的多个子公司，通过TransE模型，会得到 子公司1 ≈ 子公司2 ≈ 子公司3 的结论，但是各子公司是不同的实体，应该用不同的实体进行表示。

映射在同一个低维实值空间，同时可能收敛时间较长，甚至不会收敛，尤其是当d取值较低时（d指映射的向量空间维度），会带来收敛问题。

2、TransH模型

为了解决TransE模型在处理一对多 、 多对一 、多对多复杂关系时的局限性，TransH模型提出让一个实体在不同的关系下拥有不同的表示。对于关系r，TransH模型同时使用平移向量r和超平面的法向量w_r来表示它。

3、TransR模型

虽然TransH模型使每个实体在不同关系下拥有了不同的表示，它仍然假设实体和关系处于相同的语义空间中，这一定程度上限制了TransH的表示能力。TransR模型则认为，一个实体是多种属性的综合体，不同关系关注实体的不同属性。TransR认为不同的关系拥有不同的语义空间。对每个三元组，首先应将实体投影到对应的关系空间中，然后再建立从头实体到尾实体的翻译关系。

虽然TransR模型较TransE和TransH有显著改进，它仍然有很多缺点:

• 在同一个关系:下，头、尾实体共享相同的投影矩阵。然而，一个关系的头、尾实体的类型或属性可能差异巨大.例如，对于三元组(美国，总统，奥巴马)，美国和奥巴马的类型完全不同，一个是国家，一个是人物。

• 从实体空间到关系空间的投影是实体和关系之间的交互过程，因此TransR让投影矩阵仅与关系有关是不合理的。

• 与TransE和TransH相比，TransR由于引入了空间投影，使得TransR模型参数急剧增加，计算复杂度大大提高。