Eigen库的学习使用

环境准备

在虚拟机上安装Eigen
sudo apt-get install libeigen3-dev
下载好视觉SLAM十四讲对应的代码后，下载KDevelop，KDevelop位于Ubuntu系统的软件仓库，可以使用apt-get来安装。

1.打开project，选择对应目录下的CMakeLists.txt。

会生成build目录：

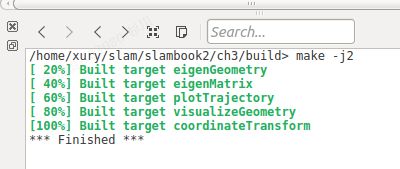
2.build该工程

报错1： By not providing “FindPangolin.cmake” in CMAKE_MODULE_PATH this project has asked CMake to find a package configuration file provided by “Pangolin”, but CMake did not find one.
没有Pangolin导致(Pangolin是对OpenGL进行封装的轻量级的OpenGL输入/输出和视频显示的库。可以用于3D视觉和3D导航的视觉图，可以输入各种类型的视频、并且可以保留视频和输入数据用于debug。)之前复现ORB_SLAM2的时候因为版本的问题安装这个库搞了很久，所以这次之前复用之前的方法。
step1：安装依赖项

sudo apt-get install libglew-dev libpython2.7-dev

step2：到github官网上下载0.5版本的Pangolin，解压后到该目录下。

cd Pangolin
mkdir build
cd build
cmake ..
make -j16
sudo make install

报错2：

添加头文件#include

编译成功：

3.执行程序

1.在run-——>Current Launch Configuration中配置选择要执行的文件。

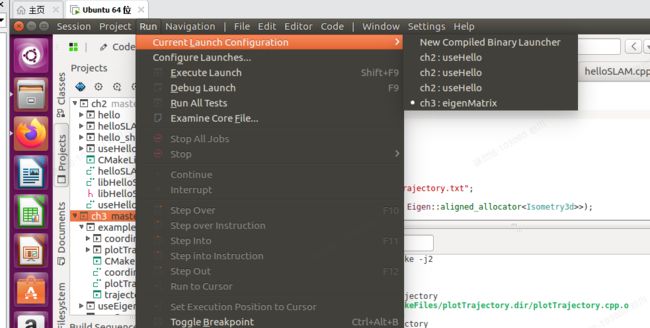
Executable中选择build目录下生成的可执行文件，最后在Launch Configurations选择要执行的文件，点击界面中的"Execute"即可。

执行结果：

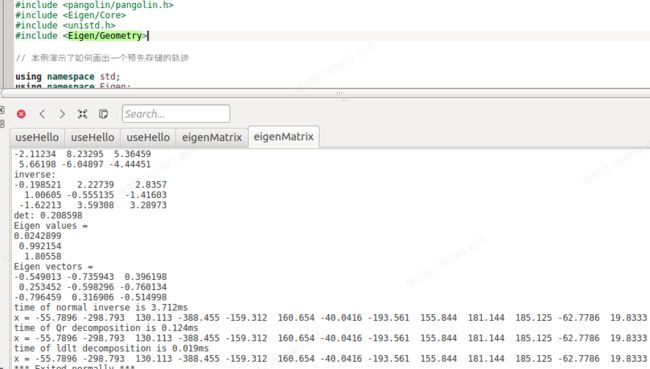
编程学习

KDevelop常用的快捷键，可以在setting中的configure shortcuts设置。
win+left 上次访问的上下文
win+right 下次访问的上下文
Ctrl+d 注释
Ctrl+Shift+d 解注释
F9运行程序

使用Eigen的头文件

//Eigen的核心部分
#include
//稠密矩阵的代数运算（逆、特征值等）
#include
//Eigen的几何模块，提供各种旋转和平移的表示
#include

1.动态矩阵和静态矩阵的定义和初始化

//定义并初始化一个2*3的矩阵
Matrix<float,2,3> matrix_23;
matrix_23 << 1,2,3,4,5,6;

//定义一个动态矩阵
MatrixXd matrixXd;
Matrix<double,Dynamic,Dynamic> matrix_dynamic;

//向量的定义,Vector3d实质是Matrix
Vector3d v_3d;
v_3d<<3,2,1;
Vector4d v_4d;

2.如何访问并操作矩阵中的元素

//访问第2行第1列的元素
cout<<matrix_23(2,1);
//假设m是一个3*3的矩阵并已经初始化，对里面的元素进行操作
m(0, 0) = 1;
m(0, 1) = 2;
m(1, 0) = m(0, 0) + 3;
m(1, 1) = m(0, 0) * m(0, 1);

3.如何使元素类型不同的矩阵相乘（float和double）

//用cast()显示转换
Matrix<double,2,1> result = matrix_23.cast<double>()*v_3d;

4.求矩阵的转置、和、迹、逆、行列式等基本操作

Matrix3d matrix_33 = Matrix3d::Random();//随机数矩阵
Matrix3d matrix_33_other = Matrix3d::Random();//随机数矩阵
cout << "random matrix: \n" << matrix_33 << endl;
cout << "transpose: \n" << matrix_33.transpose() << endl;      // 转置
cout << "sum: " << matrix_33.sum() << endl;            // 各元素和
cout << "trace: " << matrix_33.trace() << endl;          // 迹
cout << "times 10: \n" << 10 * matrix_33 << endl;               // 数乘
cout << "inverse: \n" << matrix_33.inverse() << endl;        // 逆
cout << "det: " << matrix_33.determinant() << endl;    // 行列式
cout << "det: " << matrix_33.conjugate() << endl;    // 共轭矩阵
cout << "det: " << matrix_33.adjoint() << endl;    // 伴随矩阵
cout << "det: " << matrix_33.mincoeff() << endl;    // 最小值
cout << "det: " << matrix_33.maxcoeff() << endl;    // 最大值
cout << "det: " << matrix_33.mean() << endl;    // 平均值
cout << "det: " << matrix_33.prod() << endl;    // 所有元素求积
cout << "det: " << matrix_33.dot(matrix_33_other ) << endl;    // 点乘
cout << "det: " << matrix_33.cross(matrix_33_other ) << endl;    // 叉乘

5.求矩阵的特征值和特征向量

Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);
cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl << endl;

6.解方程

  // 解方程
  // 我们求解 matrix_NN * x = v_Nd 这个方程
  // N的大小在前边的宏里定义，它由随机数生成
  // 直接求逆自然是最直接的，但是求逆运算量大
  Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
  matrix_NN = matrix_NN * matrix_NN.transpose();  // 保证半正定
  Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);
  // 直接求逆
  Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;
  cout << "x = " << x.transpose() << endl;
  // 通常用矩阵分解来求，例如QR分解，速度会快很多
  x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
  cout << "x = " << x.transpose() << endl;
  // 对于正定矩阵，还可以用cholesky分解来解方程
  x = matrix_NN.ldlt().solve(v_Nd);
  cout << "x = " << x.transpose() << endl;

7.旋转矩阵、旋转向量、四元数、欧拉角的定义和之间的转换

//1.定义旋转矩阵和旋转向量，将旋转向量转为旋转矩阵
Matrix3d rotation_matrix = Matrix3d::Identity();
AngleAxisd rotation_vector =(M_PI/4,Vector3d(0,0,1));
//.matrix()将旋转向量转为旋转矩阵
cout<<rotation_vector.matrix()<<endl;
//.toRotationMatrix()也可以将旋转向量转为旋转矩阵
rotation_matrix = rotation_vector.toRotationMatrix();

//现在有一个三维向量，利用旋转矩阵、旋转向量、欧式变换矩阵分别对其进行坐标变换
Vector3d v(1,0,0);
//旋转向量进行坐标变换
Vector3d v_rotated = rotation_vector*v;
//旋转矩阵进行坐标变换
v_rotated = rotation_matrix*v;
//用欧式变换矩阵进行坐标变换
Isometry3d T = Isometry3d::Identity();
T.rotate(rotation_vector);
T.pretanslate(Vector3d(1,3,4));
//相当于Rv+t
Vector3d v_tranformed = T*v

//将旋转矩阵转为欧拉角 按ZYX顺序 roll pitch yow
Vector3d enlur_angle = rotation_matrix.enlurAngles(2,1,0);

//把旋转矩阵或旋转向量赋值给四元数
Quaterniond q = Quaterniond(rotation_vector);
q = Quaterniond(rotation_matrix);
//使用四元数旋转一个向量
v_rotated = q*v;
//用四元数和平移向量表示两个坐标系的变换关系，怎么进行坐标转换
Quaterniond q1(0.35, 0.2,0.3,0.1),q2(-0.5,0.4,-0.1,0.2);
q1.normalize();
q2.normalize();
Vector3d t1(0.3,0.1,0.1),t2(-0.1,0.5,0.3);
Vector3d p1(0.5,0,0.2);
//得到机器人坐标系1、2到世界坐标系的变换矩阵
Isometry3d T1w(q1),T2w(q2);
T1w.pretranslate(t1);
T2w.pretranslate(t2);
//将机器人坐标系p1转到机器人坐标系p2
Vector3d p2 = T2w * T1w.inverse() * p1;
cout<<p2.transpose()<<endl;