189.轮转数组（力扣）详解-JAVA

189.轮转数组（力扣）详解-JAVA

轮转数组的三种解法

首先我们要明白一点，当k 是 nums.length倍数的时候，就相当于没有旋转。所以实际旋转的次数 是 k % nums.length

1. 翻转实现
例子：nums= [1,20,3,2,4]，k=2；
a. 整体翻转 [4,2,3,20,1]
b. (1-2)翻转[2,4]
c. (3-5)翻转[1,20,3]
d. 合并[2,4,1,20,3]
2. 使用额外数组取余
数组下标 i =0~4；k=2；（i+k）% length=2,3,4,0,1 — 对应原数组轮换后的结果数组下标
3. 环状替换
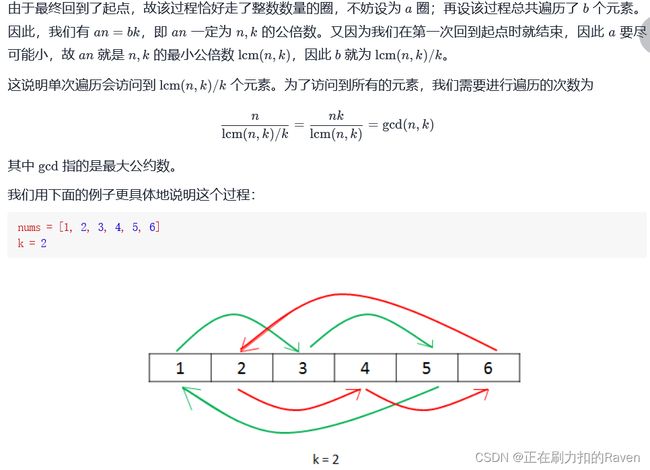
由下标0开始，将当前元素放至结果位置 next（next=(current+k)%n），再从next位置开始重复遍历直至回到开始位置。但是从0开始 到0结束的一次循环可能并没有遍历到所有的数。如：当n是k的倍数时，需要多次重复count=gcd(n,k)次上述循环直至每一个数都被遍历到。
==因为an是n,k的公倍数是一定的，又因为遍历次数要尽可能小，所以an是n，k的最小公倍数。==因为an=bk，b=an/k=lcm(n,k)/k（lcm(n,k)是n,k的最小公倍数=an）即单次遍历会访问到 b=lcm(n,k)/k个元素，为访问到所有元素，需进行count=n/b=n/lcm(n,k)/k次；nk/lcm(n,k)是n，k的最大公约数=gcm(n,k)=count

以上三种方法实现代码（Java）

1. 翻转实现代码

public static void rotate(int[] nums, int k) {
		int n=nums.length;
  	k=k%n;//防止越界
		reverse(nums,0,n-1);
		reverse(nums,0,k-1);
		reverse(nums,k,n-1);
	}

	private static void reverse(int[] nums, int i, int j) {
		int n=nums.length;
		while(i<j) {
			int temp=nums[i];
			nums[i]=nums[j];
			nums[j]=temp;
			i++;
			j--;
		}
	}

2. 使用额外数组取余实现代码

public static int[] rotate(int[] nums, int k) {
		int n=nums.length;
		int[] newArr=new int[n];
		for(int i=0;i<n;i++) {
			newArr[(i+k)%n]=nums[i];
		}
		return newArr;
	}

3. 环状替换实现代码

public static void rotate(int[] nums, int k) {
		int n = nums.length;
		k = k % n; // 令k<5;如k=6相当于k=1,k=5相当于轮转一圈没有改变
		int count = gcd(k, n); // count=k,n的最大公约数
							   // count表示需重复count次下列for循环才能遍历所有的数
		for (int start = 0; start < count; ++start) {
			int current = start; // 位置current的元素会放至 next=(current+k)%n的位置 
			int prev = nums[start];
			do {
				int next = (current + k) % n;
				int temp = nums[next];
				nums[next] = prev; // 完成next位置的更新
				prev = temp;
				current = next; // 再从next位置重复操作
			} while (start != current); // start恒等于0，循环至初始位置0时中断本次while循环
		}
	}

	public static int gcd(int x, int y) {
		return y > 0 ? gcd(y, x % y) : x;
	}

注意事项

k若大于n，可能会出现数组下标越界的情况，因此需对k做k=k%n处理