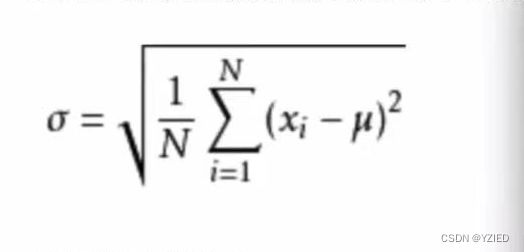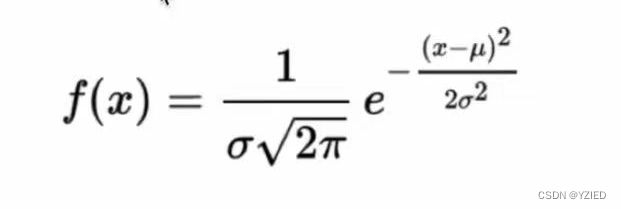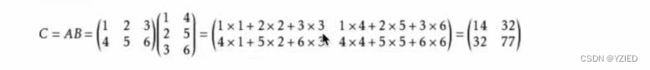Numpy

Numpy

1.Numpy的介绍

①Numpy是一个科学计算库，用于快速处理任意维度的数组

②支持常见的数组和矩阵操作

2.ndarray

1.ndarray的说明

①提供了一个N维数组类型ndarray，描述了相同类型的items的集合

②array中存储一个列表，列表中有存放多个列表

    import numpy as np
    #array中存储一个列表，列表中有存放多个列表
    score = np.array([[80, 79, 60, 98, 99],
                      [80, 79, 60, 98, 99],
                      [80, 79, 60, 98, 99],
                      [80, 79, 60, 98, 99],
                      [80, 79, 60, 98, 99],
                      [80, 79, 60, 98, 99],
                      [80, 79, 60, 98, 99],
                      [80, 79, 60, 98, 99]])
    #输出列表
    print(score)
    
#比较使用nunpy与list效率的比较
import numpy as np
import random
import time

# 由于要生成随机数组和计时，因此我们导入random和time包
a = []
# 生成10000000个随机数放入数组
for i in range(10000000):
    # 利用random.random()来生成随机数
    a.append(random.random())
t1 = time.time()
sum_number = sum(a)
t2 = time.time()
print(sum_number)
nparray = np.array(a)
d1 = time.time()
sum_array = sum(nparray)
d2 = time.time()
print(t2 - t2)
print(d2 - d1)
print(sum_array)

③列表与ndarray的比较

​ 存储风格：ndarray存储相同数据类型，list存储不同数据类型

​ 并行化运算：ndarray支持向量(并行)化运算

​ 底层语言：ndarray底层使用c语言，解除了GIL

④ndarray一般用于处于数字，很少用于处理字符串

2.nuarray的常用属性

①ndarray的常用属性有：shape(数组维度的元组)、ndim(数组维度)、size(数组中的元素数量)、itemsize(一个数组元素的长度)、dtype(数组元素类型)，可以通过 变量.属性 的方式对属性进行查看，其中shape和dtype最常用

import numpy as np

score = np.array([[80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99]])
# 查看ndarray的形状
print(score.shape)  # (8, 5)
# 查看ndarray的维度
print(score.ndim)  # 2
# 查看ndarray的元素个数
print(score.size)  # 40
# 查看ndarray的类型：在创建ndarray时没有主动指定类型，如果是数值型则为int32/64
print(score.dtype)  # int32

1.shape–数组的形状

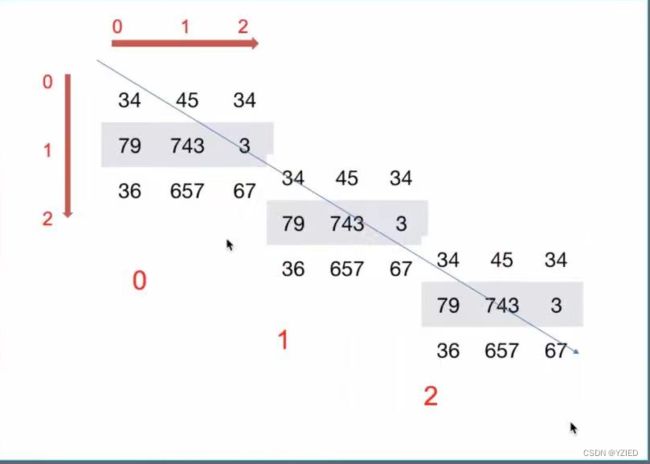
①几个维度：最简单的方法是看左侧有几个[

②每一个数字表示该维度的元素个数

import numpy as np
# 每一个数字表示该维度的元素个数
# 几个维度：最简单的方法是看左侧有几个[
a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([1, 2, 3, 4])
c = np.array([[[1, 2, 3], [4, 5, 6]], [[1, 2, 3], [4, 5, 6]]])
print(a.shape)  # (2, 3)
print(b.shape)  # (4,)：维度为，1,因此用一个数字表示，元素个数为4，由于表示形式为元组，因此只有一个数字时要加一个逗号
print(c.shape)  # (2, 2, 3):

③nparray三位数组结构：先看有几个数组，然后再看每个数组中有几个维度，最后看有几个元素

2.dtype–数组的类型

①在创建ndarray时没有主动指定类型，如果是数值型则为int32/64，浮点型为float32/64

②可以在创建数组时来指定类型

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]],dtype='float32')
b = np.array([1, 2, 3, 4],dtype=np.float32)

3.Numpy的基本操作

①numpy的操作方式有两种：

​ ndarray.方法()

​ np.函数名()

1.生成数组的方法

1.生成0和1

①生成一组0–np.zeros(shape=(a,b),dtype=‘类型’)

​ 生成一组1–np.ones(shape=(a,b),dtype=‘类型’)

​ 其中shape可以是元组或列表

import numpy as np

# 生成一组0--np.zeros(shape) 生成一组1--np.ones(shape),其中shape可以是元组或列表
zeros_array = np.zeros(shape=(3, 4))
zeros_array1 = np.zeros(shape=[3, 4], dtype='float32')
print(zeros_array)
print(zeros_array1)

one_list = np.ones(shape=(2, 3))
one_list1 = np.ones(shape=[2, 3])
print(one_list)
print(one_list1)

2.从现有数组中生成

①从现有数组中生成：

​ np.array() ,

​ np.copy() ,

​ np.asarray()，

​ 括号中可以是一个现有的数组，也可以将自己手写进去

②其中np.array() np.copy()为深拷贝，拷贝成功后再修改原数组不会对这两个方式生成的数组的值造成影响；np.asarray()为浅拷贝，即便是生成后元素组再被修改，该数组的相应元素也会修改

③使用索引进行获取与修改，下标从0开始

④np.array()最常用

import numpy as np

# 从现有数组中生成：np.array() np.copy()    np.asarray()，括号中可以是一个现有的数组，也可以将自己手写进去
# 其中np.array() np.copy()为深拷贝，拷贝成功后再修改原数组不会对这两个方式生成的数组的值造成影响；np.asarray()为浅拷贝，即便是生成后元素组再被修改，该数组的相应元素也会修改
# 利用手写先生成一个数组
score = np.array([[80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99],
                  [80, 79, 60, 98, 99]])
# 从现有数组中生成
score1 = np.array(score)
score2 = np.copy(score)
score3 = np.asarray(score)
score[2, 1] = 90  # 利用索引进行获取与修改，下标从0开始
print(score1)  # 第三行第二列元素未改变为90
print(score2)  # 第三行第二列元素未改变为90
print(score3)  # 第三行第二列元素改变为90

3.生成固定范围的数组

①生成固定范围的数组：

​ np.linspace(min,max,count)：生成从min到max(都可以取到)等距离的count个元素

​ np.arange(a,b,size)：生成从a到b(左闭右开)步长为size的元素，a，b如果写ing型则为整型，float型则为float型，如果只写一个参数则该参数参数表示b

# 生成固定范围的数组：np.linspace(min,max,count)：生成从min到max(都可以取到)等距离的count个元素
# np.arange(a,b,size)：生成从a到b(左闭右开)步长为size的元素

num1 = np.linspace(1, 10, 5)  # 从1开始每2.25生成一个数
num2 = np.arange(1, 26, 3)
num3 = np.arange(9.0)
print(num1)  # [ 1.    3.25  5.5   7.75 10.  ]
print(num2)  # [ 1  4  7 10 13 16 19 22 25]
print(num3)  # [0. 1. 2. 3. 4. 5. 6. 7. 8.]

4.生成随机数组

①分布状况：直方图可以用来表示分布状况

1.均匀分布

①均匀分布：表示每一个的可能性时相等的

②生成均匀分布数组

​ np.random.uniform(low=-1, high=1, size=100000)：均匀分布，生成从low到high之间size个随机数，size也可以传递一个shape，入size=(8,10)8行10列共80个数

import numpy as np
import matplotlib.pyplot as plt
# 均匀分布：表示每一个的可能性时相等的
# np.random.uniform(low=-1, high=1, size=100000)：均匀分布，生成从low到high之间size个随机数
data1 = np.random.uniform(low=-1, high=1, size=100000)
print(data1)

# 利用到matplotlib生成一个直方图
# 创建画布
plt.figure(figsize=(20,8),dpi=80)
# 绘制直方图
plt.hist(data1,1000)
# 显示图像
plt.show()

2.正态分布

①正态分布是具有两个参数μ和o（cgema）的连续随机变量分布，μ是服从正态分布的随机变量的均值，σ是此随机变量的方差，因此正态分布记作N（μ，σ）。方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数，可以理解为幅度、波动程度、集中程度、稳定性、离散程度的意思。方差越小越稳定，所有的数据相同时方差为0（因为数据和该数据的平均数一样，相减为0），最稳定

②u在坐标轴上表示该图形以谁做对称轴，方差越大图像越低(扁)，即数据更加分散

③生成正态分布数组：

​ np.random.normal(loc=,scale=,size=)：loc表示均值，scale表示标准差，size为形状(数值个数)

import numpy as np
import matplotlib.pyplot as plt

# np.random.normal(loc=,scale=,size=)：loc表示均值，scale表示标准差，size为形状(数值个数)
data = np.random.normal(loc=1.75, scale=0.1, size=1000)
print(data)
#也可以使用matpotlib生成直方图
plt.figure(figsize=(4, 5), dpi=60)
plt.hist(data, 100)
plt.show()

④

其中M为这组数据的平均数，s为标标准差，s的平方为一个整体即方差

⑤标准差

⑤正态分布特点

2.数组的索引、切片操作

import numpy as np
# 数组的切片、索引操作(下标从0开始)
# 一位数组获取数据及修改：将2修改为3
num = np.array([1, 2, 3])
num[1] = 3

# 二维数组获取数据及修改：获取第一个数组的前三个数据
stock_data = np.random.normal(loc=0, scale=1, size=(8, 10))
data = stock_data[0, 0:3]
data = stock_data[7, 1:3]  # [第8个维度的数据,1到2数据]
data = stock_data[0:8 , 1:3] #获取1到7行，每行获取2到3列的数据，如果是改行所有的数据则可以写成:
# 三位数组获取数据及修改：获取9，获取5，6，将2，3修改为22，33
a = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
num1 = a[1, 0, 2]
num2 = a[0, 1, 1:3]
a[0, 0, 1:3] = [22, 33]
import numpy as np

# 多维度矩阵转置：(2,4,3)矩阵进行转置则会将维列互换，即(3,4,2)：先将数组写出来，从第一个元素竖这将不同维度对应位置的数组合
a = np.array(
    [[[1, 2, 3], [13, 14, 15], [4, 5, 6], [24, 25, 26]], [[7, 8, 9], [10, 11, 12], [17, 16, 18], [34, 35, 63]]])
print(a)
b = a.T
[[[1,7],[13,10],[4,17],[24,34]] , [[2,8],[14,11],[5,16],[25,35]] , [[3,9],[15,12],[6,18],[26,63]]]

3.数组形状修改

①方式一、方式二仅会改变形状不会对行列进行转换：数组只是修改了形状,将数据按顺序重新分组并未修改顺序，如(2,3)的[1,2,3],[4,5,6]改为(3,2)的[1,2],[3,4],[5,6]

# 形状修改：让二维列表的行列反过来

# 方法一：数据变量.reshape(shape)：返回新的数组，并不会对原来的数组进行修改
new_stock_data = stock_data.reshape((10, 8))
# 方法二：数据变量.resize(shape)：对原有的数组进行修改，没有返回值,个reshape一样，只改变形状不会对行列的值进行转换
stock_data.resize((10, 8))
# 方式三：数据变量.T()：数组的转置,返回新的数组
new_stock_data = stock_data.T

4.类型的修改

①转为指定类型–数据变量.astype(‘type’)：将数组类型修改成type，返回一个新的数组，原数据不会被影响

②转为字符串类型–数据变量.tostring():将数组转换为字符串(将数据序列化到本地)，无返回值，本身为字符串但是以字节形式存储，因此相当于数据变量.tobytes()

data = np.random.normal(loc=0, scale=1, size=(8, 10))
# 转为指定类型--数据变量.astype('type')：将数组类型修改成type，返回一个新的数组，原数据不会被影响
data = data.astype('int32')
# 转为字符串类型--数据变量.tostring():将数组转换为字符串(将数据序列化到本地)，无返回值，本身为字符串但是以字节形式存储，因此相当于数据变量.tobytes()
data.tostring()
print(data.tostring())

5.数组的去重

①数组的去重：之前可以将其转换为set()，因为集合中不会有重复元素，但是numpy数组是不可以转换成set，只有一维的可以使用set进行转换，因此多维的数组需要使用unique方法

②np.unique(数据变量)：去掉数组中重复的元素，并将不重复的元素作为一个新的ndarray数组返回

# np.unique(数据变量)：去掉数组中重复的元素，并将不重复的元素作为一个新的ndarray数组返回
a = np.array([[1, 2, 3, 4], [5, 2, 2, 4]])
a = np.unique(a)
print(a)  # [1 2 3 4 5]
print(a.shape)(5, )

③多维数组使用set来去重需要先用flatten转换为一位数组，然后再用set转换为集合

​ 数据变量.flatten()：将数组变成一维的，有返回值，原数组不会造成影响

import numpy as np
a = np.array([[1, 2, 3, 4], [5, 2, 2, 4]])
# 数据变量.flatten()：将数组变成一维的，有返回值，原数组不会造成影响
a = a.flatten()  # [1 2 3 4 5 2 2 4]
# 将a转换为set去重
a = set(a)
print(a)

4.Ndarray的三大运算

1.逻辑运算

①如果想要操作符合某一条件的数据时，应该用逻辑运算

1.对每一个元素进行判断

①data表示数组中的每一个元素，使用data可以对数组中的每一个元素进行逻辑判断，并且可以将该逻辑表达式作为标记写入[]来进行批量更改

import numpy as np

data = np.random.normal(loc=0, scale=1, size=(8, 10))
# 对数组中的每一个元素进行操作，如数据变量>n:数组中的每个元素>n返回True，否则返回False，将这些True和False存入一个数组中返回
a = data > 0.5  # a的类型为ndarray
# 数据变量[条件表达式/条件比表达式返回值变量]=n：将数组中满足条件的元素改为n或其他操作
data[a] = 1.1  # 或data[data>0.5]=1.1
data[data - 0.5 > 0] = 1  # 每个元素-0.5如果大于0则将该元素设置为1

2.通用判断函数

1.np.all(布尔值)

①布尔值参数中只要有一个False就返回False，全是True则返回True

data = np.random.normal(loc=0, scale=1, size=(8, 10))
# 判断数据是否全是正数
print(np.all(data > 0))  # False

2.np.any(布尔值)

①布尔值中只要有一个True则返回True，全是False则返回False

data = np.random.normal(loc=0, scale=1, size=(8, 10))
# 判断前五行是否有整数
print(np.any(data[:5, :] > 0))  # 因为是8行10列的二维数组，所以第一个参数0:5表示1到5行，:表示0：11即全部列

3.三元运算符–np.where

①np.where(条件，value1/操作1，value2/操作2)：对元素进行判断，如果满足条件，则将其值置为valu1，如果不满足条件则将其值置为value2

②如果条件是一个符合的逻辑判断，如大于0并且小于1，或大于1或小于0等用到与和或，需要使用

np.logical_and–与

np,logical_or–或

np.logical_not–非

np.logical_xor–异或

③np.where(np.logical_and(data>0.5,data<1),1,0)

import numpy as np

data = np.random.normal(loc=0, scale=1, size=(8, 10))
# 前4行前前四列的数如果大于0置为1，否则置为2
data = np.where(data[0:4, 0:4] > 0, 1, 2)
# 前4行前前四列的数如果大于0置为对应元素+1，否则置为对应元素+10
data = np.where(data[0:4, 0:4] > 0, data[0:4, 0:4] + 1, data[0:4, 0:4] + 10)
# 前4行前前四列的数如果大于0并且小于1的元素置为对应元素+1，否则置为对应元素+10
data = np.where(np.logical_and(data[:4, :4] > 0, data[:4, :4] < 1), data[0:4, 0:4] + 1, data[0:4, 0:4] + 10)
# 可以先将前四行前四列的数据取出来，在where中直接中
temp = data[0:4, 0:4]
data = np.where(np.logical_and(temp > 0, temp < 1), data[0:4, 0:4] + 1, data[0:4, 0:4] + 10)

2.统计运算

1.统计指标函数

①min、max、median(中位数)、var（方差）、std（标准差）、mean（平均值）

②使用方式

np.函数名(数据变量,axis=0/1)：其中min、max、mean、median可以设置asix，当axis为0或-2是表示求每列的最大值，为1或-1表示求每行的最大值,不同的版本或库不一样，用的时候可以先试一下
#案例：
import numpy as np
data = np.random.normal(loc=0, scale=1, size=(8, 10))
# 求前四行四列中最大的
temp = data[0:4, 0:4]
print(np.max(temp))  # 1.80911462161872
# 求前四行四列中某一行的最大值
print(np.max(temp, axis=1))  # [0.91864224 1.66607471 1.21918327 1.80911462]

2.最大值、最小值所在位置

①np.argmax(data,axis)：返回最大值所在的位置

②np.argmin(data,axis)：返回最小值所在位置

import numpy as np
data = np.random.normal(loc=0, scale=1, size=(8, 10))
# np.argmax(data,axis)：返回最大值所在的位置
print(np.argmax(temp, axis=1))  # [3 0 2 3]
# np.argmin(data.axis)：返回最小值所在位置
print(np.argmin(temp, axis=-1))  # [0 3 1 0]

3.数组间运算

1.数组与数的运算

①在numpy中可以直接利用变量对所有元素进行操作，如果不借助numpy则需要使用for循环

import numpy as np
arr = np.array([[1, 2, 4, 5, 16, 43, 123], [1, 2, 4, 5, 14, 41, 45]])
# 在numpy中可以直接利用变量对所有元素进行操作，如果不借助numpy则需要使用for循环
arr = (arr + 100) / 1

2.数组与数组的运算

①形状相同的数组可以进行运算

②形状不同的数组满足广播机制也可以进行运算

③广播机制：

​ (1)对应维度上元素个数相等

​ (2)某一对应的维度元素个数不等，但是其中一个数组该维度元素个数为1

计算结果的形状：从对应维度中选取非1的维度，如果只有1就选1

注：观察方法：写出两个数组的shape，然后右对齐，缺数的就补1

import numpy as np

# arr1两行7列，arr2两行3列
arr1 = np.array([[1, 2, 4, 5, 16, 43, 123], [1, 2, 4, 5, 14, 41, 45]])
arr2 = np.array([1, 2, 3], [4, 5, 5])
# 两个不同形状的数组不可以直接进行运算如：arr1+arr2
# 广播机制(Broadcast)：为了放方便不同形状的ndarray进行运算，则满足一下的规则就可以进行运算
# 1.维度上元素个数相等    2某一维度上元素个数不等但元素个数为1。注从后往前排没有的补1
# 计算结果：非1的维度
# 有两个数组，首先写出维度，如果维度不齐则用1来补(即第二个数组0的位置为1),根据条件可以进行运算，运算结果为2,2,1(非1的数字)
(2, 2, 1) - -[[[1], [2]], [[3], [4]]]
(0, 0, 1) - -[1]
# 运算结果9875
(9, 1, 7, 1)
(0, 8, 1, 5)
(9, 8, 7, 5)
# 下面的不可以进行运算：不满足规则
# 第一组
(3)[1, 2, 3]
(2)[4, 5]
# 第二组
(2, 1) - [[1], [2]]
(3, 2, 3) - [[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]], [[12, 14, 15], [16, 17, 18]]]

arr1 = np.array([[[[1], [1], [3]]], [[[4], [5], [6]]]])
arr2 = np.array([[[1, 2]], [[1, 2]]])
arr3 = arr1 + arr2
# 相加结果
[[[[2 3]
   [2 3]
   [4 5]]

  [[2 3]
   [2 3]
   [4 5]]]


 [[[5 6]
   [6 7]
   [7 8]]

  [[5 6]
   [6 7]
   [7 8]]]]

3.矩阵运算

1.矩阵的说明

①矩阵必须是2维的

②矩阵一定是二维数组，二维数组不一定是矩阵

2.矩阵的存储

# 方式一：np.array(二维数组)，该方法创造出来的数组维nparray类型
arr1 = np.array([[90, 91], [85, 86], [88, 90], [90, 90], [91, 90]])  # 二维：5行2列
print(arr1, type(arr1))
# 方式二：np.mat(二维数组)，该方法创造出来的数组维matri类型
arr2 = np.mat([[90, 91], [85, 86], [88, 90], [90, 90], [91, 90]])
print(arr2, type(arr2))
[[90 91]
 [85 86]
 [88 90]
 [90 90]
 [91 90]] <class 'numpy.ndarray'>
[[90 91]
 [85 86]
 [88 90]
 [90 90]
 [91 90]] <class 'numpy.matrix'>

3.矩阵的乘法运算

①要求

形状：第一个矩阵的列数和第二个矩阵的行数相等，结果为第一个矩阵的行数第二个矩阵的列数。即(m,n)*(n,l)=(m,l)

运算规则：

import numpy as np

arr1 = np.array([[90, 91], [85, 86], [88, 90], [90, 90], [91, 90]])
arr2 = np.array([[1], [2]])
arr3 = np.mat([[90, 91], [85, 86], [88, 90], [90, 90], [91, 90]])
arr4 = np.mat([[1], [2]])
print(type(arr4))
# 方式一：np.matmul(arr1,arr2),arr1，arr2可以是不同的类型
result = np.matmul(arr1, arr2)
# 方式二：np.dot(arr1,arr2),arr1，arr2可以是不同的类型
result = np.dot(arr3, arr4)
# 方式三：如果至少包含一个matri类型可以直接用*
result = arr1 * arr4
# 方式四：如果全是nparray类型也可以使用@来代替*。因为满足广播机制，因此数组不可以做*，因此要使用矩阵的方法而不是用数组的规则
result = arr1 @ arr2

4.矩阵求逆–np.linalg.inv(arr)

①数组类型求逆:np.linalg.inv(arr)

② mat类型和数组类型求逆： arr.I

# 数组类型求逆:np.linalg.inv(arr)
a = np.array([[1, 2], [3, 4]])  # 初始化一个非奇异矩阵(数组)
print(np.linalg.inv(a))  # 对应于MATLAB中 inv() 函数

# mat类型和数组类型求逆： arr.I
A = np.mat(a)
print(A.I)
print(np.linalg.inv(A))

5.合并、分割、IO操作、数据处理(了解)

1.拼接

1.np.hstack((arr1,arr2))–水平拼接

①水平拼接要保证两个数组的行数维度一样

②拼接方式：直接拼接在数组后方

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
arr = np.hstack((arr1, arr2))
# [1,2,3] 与 [4,5,6] = [1, 2, 3, 4, 5, 6]

arr3 = np.array([[1], [2], [3]])
arr4 = np.array([[4], [5], [6]])
arr = np.hstack((arr3, arr4))
# [1] 与 [4] = [[1 4]
# [2] 与 [5] =  [2 5]
# [3] 与 [6] = [ 3 6]]

2.np.vstack((arr1,arr2))–垂直拼接

①垂直拼接要保证两个数组列数维度一样

②拼接方式：直接拼接在数字下方

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
arr = np.vstack((arr1, arr2))
#  [1,2,3]
#  [4,5,6]
#	拼接
# [[1 2 3]
#  [4 5 6]]

arr3 = np.array([[1], [2], [3]])
arr4 = np.array([[4], [5], [6]])
arr = np.vstack((arr3, arr4))
# [1]
# [2]
# [3]
# 与
# [4]
# [5]
# [6]
# 拼接
# [[1]
#  [2]
#  [3]
#  [4]
#  [5]
#  [6]]

3.np.concatenate((arr1,arr2/arr2.T),axis=0/1)–可选择拼接

①np.concatenate((arr1,arr2/arr2.T),axis=0/1):axis=0竖直拼接，axis=1水平拼接

②当两个数组不满足该拼接方式但是还想要拼接时，可以给数组进行转置

arr5 = np.array([[1, 2], [3, 4]])
arr6 = np.array([[5, 6]])
arr = np.concatenate((arr5, arr6.T), axis=1)
# [[1 2 5]
#  [3 4 6]]
arr = np.concatenate((arr5, arr6), axis=0)
# [[1 2]
#  [3 4]
#  [5 6]]

2.np.split(arr,groupcount/分割点列表)–分割

①np.split(arr, groupcount)：将arr进行分割，分成groupcount组，使用此方法进行分割时必须保证等份分割

②np.split(arr, [分割点index1,分割点index2,分割点index3…])：将arr进行分割，从分割index之前开始分割，参数二为存放分割点下标的列表

import numpy as np

# np.split(arr, groupcount)：将arr进行分割，分成groupcount组，使用此方法进行分割时必须保证等份分割
arr = np.arange(9)  # [0 1 2 3 4 5 6 7 8]
result = np.split(arr, 3)
# [array([0, 1, 2]), array([3, 4, 5]), array([6, 7, 8])]

# np.split(arr, [分割点index1,分割点index2,分割点index3...])：将arr进行分割，从分割index之前开始分割，参数二为存放分割点下标的列表
arr = np.arange(2, 9)
result = np.split(arr, [3, 4, 6, 10])
print(result)

3.IO操作与数据处理

1.np.genfromtxt(‘文件路径’,delimiter=‘分隔符’)–读取文件

①np.genfromtxt(‘文件路径’,delimiter=‘分割符’)：读取数据文件，delimiter表示用什么来进行分割,由于读取的字符串为nan因此，一般不使用

import numpy as np

# np.genfromtxt('文件路径',delimiter=',')：读取数据文件，delimiter表示用什么来进行分割,由于读取的字符串为nan因此，一般不使用
data = np.genfromtxt('D:/百度网盘/百度网盘下载内容/Python数据挖掘基础教程资料/资料二/day2资料/02-代码/test.csv',
                     delimiter=',')
# [[  nan   nan   nan   nan]
#  [  1.  123.    1.4  23. ]
#  [  2.  110.    nan  18. ]
#  [  3.    nan   2.1  19. ]]
print(type(data[2, 2]))  # 

②缺失值：当我们读取本地文件为float的时候，如果有缺失值（或None），就会出现nan，nan为float类型

③怎么处理缺失值nan

​ (1)直接删除含有缺失值得样本

​ (2)替换/插补：求nan所在列非nan数据的平均值或中位数，然后放到nan处（用pandas来完成，用numpy完成很麻烦）

def fill_nam_by_column_mean(t):
    for i in range(t.shape[1]):
        # 计算nan的个数
        nan_num = np.count_nonzero(t[:, i][t[:, i] != t[:, i]])
        if nan_num > 0:
            now_col = t[:, i]
            now_col_not_nan = now_col[np.isnan(now_col) == False].sum()
            now_col_mean = now_col_not_nan / (t.shape[0] - nan_num)
            now_col[np.isnan(now_col)] = now_col_mean
            t[:, i] = now_col
    return t
fill_nam_by_column_mean(data)
nan  18. ]
#  [  3.    nan   2.1  19. ]]
print(type(data[2, 2]))  # 

②缺失值：当我们读取本地文件为float的时候，如果有缺失值（或None），就会出现nan，nan为float类型

③怎么处理缺失值nan

​ (1)直接删除含有缺失值得样本

​ (2)替换/插补：求nan所在列非nan数据的平均值或中位数，然后放到nan处（用pandas来完成，用numpy完成很麻烦）

def fill_nam_by_column_mean(t):
    for i in range(t.shape[1]):
        # 计算nan的个数
        nan_num = np.count_nonzero(t[:, i][t[:, i] != t[:, i]])
        if nan_num > 0:
            now_col = t[:, i]
            now_col_not_nan = now_col[np.isnan(now_col) == False].sum()
            now_col_mean = now_col_not_nan / (t.shape[0] - nan_num)
            now_col[np.isnan(now_col)] = now_col_mean
            t[:, i] = now_col
    return t
fill_nam_by_column_mean(data)