LeetCode刷题笔记

前言： 2021-8-24，我开始刷LeetCode了！！！为了让自己有动力，能坚持下去，最重要的是能有人跟我一起讨论题目。于是在师兄的建议下，我拉了一个小群，带领实验室的一些小伙伴们一起刷题。虽然目前刷题的人数还不是很多，但我相信不久以后我们的队伍一定会更加壮大的。嘿嘿！！希望我们能一路坚持下去。加油！！
由于比较菜，好多题目都没思路，但并不能因为这就放弃刷题，不会就看答案，看懂了再敲代码。反复积累，经过一段时间，一定会有很多收获的。

数组

1、删除排序数组中的重复项

❤ 2021-8-24 ❤

1）题目：给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。
不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1：
输入：nums = [1,1,2]
输出：2, nums = [1,2]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

2）思路1： 对于有序数组，使用两个指针，右指针始终往右移动，
如果右指针指向的值等于左指针指向的值，左指针不动。
如果右指针指向的值不等于左指针指向的值，那么左指针往右移一步，然后再把右指针指向的值赋给左指针。原来的值被覆盖。

class Solution {
public:
	int removeDuplicates(vector<int>& nums) {
		if (nums.size() < 2)
			return nums.size();
		int left = 0;
		for (int right = left+1; right < nums.size(); right++) {
			if (nums[left] != nums[right])
				nums[++left] = nums[right];
		}
		return ++left;
		
	}
};

3）思路2： 如果是无序数组，遍历数组，让第i个元素与它后面的所有元素比较，
如果后面的元素一旦有相同的元素出现，就跳出循环让i+1跟后面所有元素比较；
如果后面的所有元素没有相同的元素，就把第i个元素存在“新数组”中

int removeDuplicates(int* nums, int numsSize) {
	int len = 0, j;
	for (int i = 0; i < numsSize; i++) {
		for (j = i + 1; j < numsSize; j++) {
			if (nums[i] == nums[j])
				break;
		}
		if (j == numsSize) {
			nums[len++] = nums[i];

		}
	}
	return len;
}

❤ 2021-8-25 ❤

2、买卖股票的最佳时机

1）题目： 给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

2）思路： 想要获利最大就要高抛低吸，因为我们可以提前知道下一天的价格，并且每天最多可以操作一次，而且必须在再次购买前卖掉之前的。所以只要第二天的价格比前一天高，就默认在前一天买了，第二天卖出。累积求和就是最大收益。

int maxProfit3(vector<int>& prices) {
		int length = prices.size();
		int i,sum=0;
		for (i = 1; i < length; i++) {
			if (prices[i] > prices[i - 1])
				sum += prices[i] - prices[i - 1];
		}
		return sum;
	}

❤ 2021-8-26 ❤

3、旋转数组

1）题目： 给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

2）思路1： 把前面的length-k个元素存放在新数组里
把后面的k个元素向前移动，在两个数组拼接在一起。尤其要注意 k>length 的情况

3）思路2： 把数组整体倒序；再从第K个数一分为二；k左侧倒序；k右侧也倒序

❤ 2021-8-27 ❤

4、存在重复元素

1）题目： 给定一个整数数组，判断是否存在重复元素。
如果存在一值在数组中出现至少两次，函数返回 true 。如果数组中每个元素都不相同，则返回 false 。
示例 1:
输入: [1,2,3,1]
输出: true

2）思路一： 两层遍历，明显超时；
3）思路二： 先给数组排序，这样相同的元素就挨在一起了，所以只要比较相邻元素就行了。

❤ 2021-8-28 ❤

5、只出现一次的数字

1）题目： 给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
说明：
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？
示例 1:
输入: [2,2,1]
输出: 1

2）思路1： 开始以为先排序，这样有相同的就挨在一起了了；如果这个元素跟他的上一个元素不同，而且跟他的下一个元素也不同，那么就出现了一次。第一个元素和最后一个元素单独考虑。
提交错误：提示考虑情况不全面。

3）思路2： 进行异或运算
首先针对异或运算，这里做一个知识点的总结：
任何数和自己做异或运算，结果为 0，即 a⊕a = 0 。
任何数和 0 做异或运算，结果还是自己，即 a⊕0 = a。
异或运算中，满足交换律和结合律，也就是 a⊕b⊕a = b⊕a⊕a = b⊕(a⊕a) = b⊕0 =b。

❤ 2021-8-29 ❤

6、两个数组的交集

1）题目： 给定两个数组，编写一个函数来计算它们的交集。
示例 1：
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]

2）思路：

class Solution {
public:
	vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
		//先对两个数组进行排序
		sort(nums1.begin(), nums1.end());
		sort(nums2.begin(), nums2.end());
		int length1 = nums1.size(), length2 = nums2.size(),p=0;
		//int* result = new int[];
		vector<int> result;
		//定义上下两个指针,当他们任意一个大于长度时终止循环
		int i=0, j=0;
		while (i<length1 && j<length2)
		{
			if (nums1[i] < nums2[j]) {
				//如果i指向的值小于j指向的值说明，i向右移动
				++i;
			}
			else if (nums1[i] > nums2[j])
			{
				//如果i指向的值大于j指向的值说明，j向右移动
				++j;
			}
			else
			{
				// 如果i和j指向的值相同，说明这两个值是重复的，
				// 把他加入到集合中，然后i和j同时都往后移一步
				result.push_back (nums1[i]);
				++i;
				++j;
			}	
		}
		return result;
	}
};

❤ 2021-8-31 ❤

7、加一

1）题目： 给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。
最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外，这个整数不会以零开头。
示例 1：
输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。

2）思路： 数组采用倒序“遍历”的方式
如果数组的最后一个数字不是9，那么就直接加1，返回该数组；
如果是9，就把该位变成0，数组的上一位加1；
如果数组的所有位都是9，那么数组的长度要加1；

class Solution {
public:
	vector<int> plusOne(vector<int>& digits) {
		int length = digits.size();
		for (int i = length - 1; i >= 0; i--) {
			if (digits[i] != 9) {
				digits[i] += 1;
				return digits;
			}
			else
			{
				digits[i] = 0;
			}
		}
		digits[0] = 1;
		digits.push_back(0);
		return digits;
	}
};

❤ 2021-9-1 ❤
9月的第一天真是开门红，今天在完全没有看答案的情况下，自己完整的做出了一道题。真的超级开心！！坚持还是有效果的。继续加油！真是一个不错的开始！

8、移动零

1）题目： 给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
必须在原数组上操作，不能拷贝额外的数组。
尽量减少操作次数

2）思路1： 遍历数组；如果该位不是0，就把他放在一个“新数组”（此处的新数组并不是新开辟一个数组空间）里面；如果非0数组的长度小于原来数组的长度就把其他位都变为0；

class Solution {
public:
	void moveZeroes(vector<int>& nums) {
		//先记下数组长度
		int length = nums.size();
		//记录非0数组的长度
		int j = 0;
		//找出不是0的数依次排在数组中
		for (int i = 0; i < length; ++i) {
			if (nums[i] != 0) {
				nums[j++] = nums[i];
			}
		}
		//把其余位都变为0
		while (j<length)
		{
			nums[j++] = 0;
		}
	}
};

2）思路2： 双指针，第一个指针 i 记录0的位置，第二个指针 j 遍历数组，遇到0不管，遇见不是0的就和他前一个是0的（也就是nums[i]）交换值。
注意： 交换时 nums[j] = temp 不是 = 0；否则 数组是 {1} 就执行错误了。

void moveZeroes2(vector<int>& nums) {
		//双指针，遍历数组，遇到0不管，遇见不是0的就和他前一个是0的交换值
		int length = nums.size();
		int i=0;
		for (int j = 0; j < length; ++j) {
			if (nums[j] != 0) {
				int temp = nums[i];
				nums[i] = nums[j];
				nums[j] = temp;
				++i;
			}
		}
	}

❤ 2021-9-2 ❤

9、两数之和

1）题目：

2）思路1： 两层for循环，这是最容易想到的，但很费时间，要388ms。

	vector<int> twoSum(vector<int>& nums, int target) {
		vector<int> result;
		int length = nums.size();
		int i, j;
		for (i = 0; i < length; ++i) {
			for ( j = i+1; j < length; j++)
			{
				if (nums[i] + nums[j] == target) {
					result.push_back(i);
					result.push_back(j);
					return result;
				}

			}
		}
		//没有这行会报错
		return { i,j };
	}

3）思路2： 使用两次哈希表

vector<int> twoSum2(vector<int>& nums, int target) {
		//创建哈希表存放数组元素
		map<int, int> a;
		vector <int> result;
		//把数据放入哈希表中，关键字是nums[i],值是i
		for (int i = 0; i < nums.size(); i++) {
			//a.insert(map::value_type(nums[i], i));
			a[nums[i]] = i;
		}
		//在哈希表中查找目标元素
		for (int i = 0; i < nums.size(); i++) {
			//目标元素target-nums[i]出现的次数大于0，并且目标元素不能是本身
			if (a.count(target - nums[i]) > 0 && a[target - nums[i]] != i) {
				result.push_back(i);
				result.push_back(a[target - nums[i]]);
				//找到一组值跳出循环，否则会返回4个值
				break;
			}
		}
		return result;
	}

注：
1、使用map函数要引入 map的命名空间

#include 

2、count函数用于返回指定元素出现的次数。
3、if (a.count(target - nums[i]) > 0 && a[target - nums[i]] != i)是为了查到它本身。
比如数组是 [3,2,4] 目标值是 6,3+3=6,所以要避免它查找自身。

3）思路3： 使用一次哈希表，边找边存，先找再存。

vector<int> twoSum3(vector<int>& nums, int target) {
		//创建哈希表存放数组元素
		map<int, int> a;
		vector <int> result;
		int i;
		//在哈希表中查找目标元素
		for (i = 0; i < nums.size(); i++) {
			//目标元素target-nums[i]出现的次数大于0
			if (a.count(target - nums[i]) > 0) {
				result.push_back(a[target - nums[i]]);
				result.push_back(i);
				//找到一组值跳出循环，否则会返回4个值
				break;
			}
			//反过来放入map中，用来获取结果下标
			a[nums[i]] = i;
		}
		return result;
	}

❤ 2021-9-3 ❤

10、有效数独

1）题目：


2）思路： 今天没有想出思路，o(╥﹏╥)o看了一位大佬的解题思路：依次遍历求解

class Solution {
public:
	bool isValidSudoku(vector<vector<char>>& board) {
		//第一个参数表示行数（或列数、或盒子数）
		//第二个参数存放的是0-9之间任意一个数
		int row[9][10] = { 0 };//存储每一行的每个数是否出现过
		int col[9][10] = { 0 };//存储每一列的每个数是否出现过
		int box[9][10] = { 0 };//存储每一个3*3的box的每个数是否出现过
		for (int i = 0; i < 9; i++)
		{
			for (int  j = 0; j < 9; j++)
			{
				if (board[i][j] == '.')
					continue;
				int number = board[i][j] -'0';
				if (row[i][number])
					return false;
				if (col[j][number])
					return false;
				if (box[j / 3 + (i / 3) * 3][number])
					return false;
				//之前没出现过，现在出现了就置1，下次再row、col或box中再出现时就会返回false。
				row[i][number] = 1;
				col[j][number] = 1;
				box[j / 3 + (i / 3) * 3][number] = 1;
			}
		}
		return true;
		
	}
};

3）总结： 与昨天题目的思路3类似。row、col、box的第一个参数相当于哈希表的键（关键字），第二个参数相当于键值。
int number = board[i][j] -‘0’; board里面存的是一个char类型的数，它的ASCI码减去0的ASCI码，正好是其存放的数（0-9之间的一个数字）。
box[j / 3 + (i / 3) * 3][number] 第一个参数的设定，解释请参考链接。

❤ 2021-9-5 ❤

11、旋转图像

1）题目： 中等难度

2）思路一：
很容易看出来，第 J 行转化后变成了倒数第 J 行；
再具体到每一个元素上 ，第 i 行第 j 列转化后成了第 j 行第 (length-1-i) 列。
可以先把原数组拷贝一份。（c++中的拷贝函数是 auto）

class Solution {
public:
	void rotate(vector<vector<int>>& matrix) {
		//翻转后第I行变成了倒数第I列
		//第I行第J列的元素变为第J行第（length-1-i)列的元素
		//把原数组拷贝一下；
		auto matrix_new = matrix;
		int length = matrix.size();
		for (int i = 0; i < length; i++)
		{
			for (int j = 0; j < length; j++)
			{
				matrix[j][length - 1 - i]= matrix_new[i][j];
			}

		}
		}
	}

3）思路二：
在思路一关键式（matrix[j][length - 1 - i]= matrix_new[i][j];） 的基础上原地旋转
从最外层开始旋转，四个数为一组旋转，以3*3矩阵为例，（1,3，9,7）为一组，（2,6，8,4）为一组，5自己一组。找着四个数的位置关系。最主要的是旋转多少次，即 i,j 的最大值。

	void rotate2(vector<vector<int>>& matrix) {
		int length = matrix.size();
		//注意i和j的范围
		for (int i = 0; i < length/2; i++)
		{
			for (int j = 0; j < (length+1)/2; j++) {
				int temp = matrix[i][j];
				matrix[i][j] = matrix[length - 1 - j][i];
				matrix[length - 1 - j][i] = matrix[length - 1 - i][length - 1 - j];
				matrix[length - 1 - i][length - 1 - j] = matrix[j][length - 1 - i];
				matrix[j][length - 1 - i] = temp;
			}
		}
		
	}

3）思路三：
把原矩阵 倒着按第一列（7,4，1），第二列（8,5，2），第三列（9,6，3）…的顺序存放在 一个一维数组中。数组变为（7,4，1,8，5,2，9,6，3）；再把数组中的值赋值给矩阵。

void rotate3(vector<vector<int>>& matrix) {
		int length = matrix.size();
		vector<int> temp;
		for (int j = 0; j < length ; j++)
		{
			for (int i = length-1; i>=0 ; i--) {
				temp.push_back(matrix[i][j]);
			}
		}
		for (int i = 0; i < length; i++)
		{
			for (int j = 0; j < length; j++)
			{
				matrix[i][j] = temp[i * length + j];
			}

		}
	}

字符串

❤ 2021-9-6 ❤

1、反转字符串

1）题目： 简单

2）思路一：沿对称轴翻转，S[i] 和 S[length-1-i] 互换就是反转后的结果。

void reverseString(vector<char>& s) {
		//沿对称轴交换
		int length = s.size();
		for (int i = 0; i < length/2; i++)
		{
			swap(s[i], s[length - 1 - i]);
		}
	}

3）思路二： 双指针；首端一个left，末端一个right，交换两个数，并且left向右移，right向左移，直到left>right;

void reverseString(vector<char>& s) {
		int length = s.size();
		int i = 0,j=length-1;
		while (i<j)
		{
			swap(s[i], s[j]);
			++i;
			--j;
		}
	}

❤ 2021-9-7 ❤

2、整数反转

1）题目： 简单（并不觉得简单，o(╥﹏╥)o 我太菜了！）

2）思路一： 我开始认真思考了一下这道题，觉得思路并不难。
首先，把 int 型数字与10进行取余得到每一位的数字，再把这些数字存放到 vector 向量中；
然后，根据向量下标与进制的关系输出。

int reverse2(int x) {
		double result = 0;
		vector<char> buf;
		while (x > 0)
		{
			buf.push_back(x % 10);
			x = x / 10;
		}
		int length = buf.size();
		for (int i = 0; i < length; i++)
		{
			result += buf[i] * pow(10, length - 1 - i);
			//如果超出int存储的范围，返回0；
			if (result > (pow(2, 31) - 1) || result < pow(-2, 31))
				return 0;
		}
		
		return result;
	}

但是，这种情况不能让处理负数，为了能同时处理正负数，我把上面的代码封装成了一个函数，让下面的代码调用它。

	int reverse(int x) {

		if (x > (pow(2, 31) - 1) || x < -pow(2, 31))
		{
		return 0;
		}
		else if (x < 0) {
			int t = -1;
			x = -x;
			return t * reverse2(x);
		}
		else
		{
			return reverse2(x);
		}
	}

本以为这就成功了，但是当输入的 x 超出 int 的范围
就会报错。想了半天也没有找出原因，无奈地点开来官方答案。
3）思路二： 官方是这样说的 整数反转

class Solution {
public:
	int reverse(int x) {
		int rev = 0;
		while (x != 0) {
			if (rev < INT_MIN / 10 || rev > INT_MAX / 10) {
				return 0;
			}
			int digit = x % 10;
			x /= 10;
			rev = rev * 10 + digit;
		}
		return rev;
	}
};

❤2021-9-8 ❤

3、字符串中的第一个唯一字符

1）题目： 简单

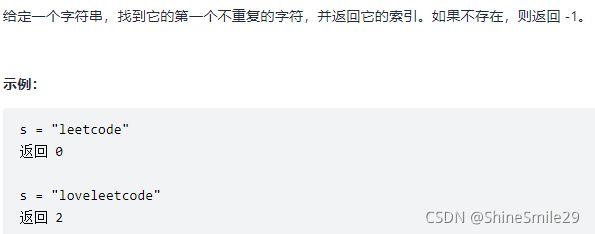
2）思路一： 32ms 双指针，指针 i 指向要匹配的元素，指针 j 表示待匹配的，如果是s[i]==s[j]，说明 s[i] 不是惟一的元素，则i++，让下一个元素再依次匹配。

int firstUniqChar(string s) {
		int j,i = 0;
		int length = s.size();
		while (i<length)
		{
			for ( j = 0; j < length ; j++) {
				if (s[i] == s[j] && j != i) 
					break;	
			}
			if (j == length)
				return i;
			else
			{
				++i;
			}
		}
		return -1;	
	}

下面是官方思路。
3）思路二： 64ms 对字符串进行两次遍历，第一次记录下每个字符出现的次数，并存入哈希表中；第二次遍历，我们只要遍历到了一个只出现一次的字符，那么就返回它的索引，否则在遍历结束后返回 −1。
键是存入的字符，键值是字符出现的次数。

int firstUniqChar2(string s) {
		int length = s.size();
		map<int, int>frequence;
		for (char ch:s)
		{
			++frequence[ch];
		}
		for (int i = 0; i < length; i++)
		{
			if (frequence[s[i]] == 1)
				return i;
		}
		return -1;
	}

注意： 此处有一种新的循环方式 for (char c : s)
这是C++11中新增的一种循环写法，对数组(或容器类,如vector和array)的每个元素执行相同的操作，此外string类也支持这种对字符的遍历循环操作。
如: double prices[5] = {4.99,5.99,6.99,7.99,8.99};
for(double x:prices)
cout << x << endl;
其中,x最初表示数组prices的第一个元素,显示第一个元素后,不断执行循环,而x依次表示数组的其他元素。

4）思路三： 84ms 第一次将数据存入哈希表，键是字符，键值是索引；如果字符已存在，就将其索引值改为-1；否则就将其存入数组中。第二次遍历，查找键值不是 -1，并返回最小的索引值。

int firstUniqChar3(string s) {
		int length = s.size();
		map<int, int> position;
		for (int i = 0; i < length; i++)
		{
			if (position.count(s[i]))
				position[s[i]] = -1;
			else
			{
				position[s[i]] = i;
			}
		}
		for (int i = 0; i < length; i++)
		{
			if (position[s[i]] != -1)
				return i;

		}
		return -1;
	}

5）思路四： 80ms 队列 先进先出 ，很适合用来找出第一个满足某个条件的元素。

int firstUniqChar4(string s) {
		int length = s.size();
		map<int, int>position;
		//pair是将2个数据组合成一组数据放在queue中
		queue<pair<char, int>> q;
		for (int i = 0; i < length; i++)
		{
			//如果哈希表中没有S[I]就存入，并插入队列
			if (!position.count(s[i])) {
				position[s[i]] = i;
				q.emplace(s[i], i);
			}
			//如果哈希表中有S[I]，就把键值设为-1，如果队列非空并且该值在队列的队首就移除。
			//注意在队首才移除
			else
			{
				position[s[i]] = -1;
				while (!q.empty()&&position[q.front().first]==-1)
				{
					q.pop();
				}
			}
		}
		return q.empty() ? -1 : q.front().second;
	}

❤ 2021-9-10 ❤

1）题目： 简单

2）思路一： 创建两个哈希表，键是字符，键值是字符出现的次数，一个存放 s 的，一个存放 t 的，比较两个哈斯表是不是一样。
太费时间了，要24ms。

bool isAnagram(string s, string t) {
		map<char, int> str1;
		map<char, int> str2;
		int length = s.size();
		if (s.size() != t.size())
			return false;
		for (int i = 0; i < length; i++)
		{
			++str1[s[i]] ;
			++str2[t[i]];
		}
		for (int i = 0; i < length; i++)
		{
			if (str1!=str2)
				return false;
		}
		return true;
	}

3)思路二： 创建两个向量，分别存放 s 和 t 的的 ASCII 码；在对两个向量进行排序，看两个向量是否相同。
16ms ,时间还是有点长。

bool isAnagram2(string s, string t) {
		vector<int> buf1;
		vector<int> buf2;
		int length=s.size();
		if (s.size() != t.size())
			return false;
		for (int i = 0; i < length; i++)
		{
			buf1.push_back(s[i] - 'a');
			buf2.push_back(t[i] - 'a');
		}
		sort(buf1.begin(), buf1.end());
		sort(buf2.begin(), buf2.end());
		if (buf1 != buf2)
			return false;
		return true;
	}

4）思路三： 后来才知道可以直接对字符进行排序。
但是时间也没少多少，12ms.

	bool isAnagram3(string s, string t) {
		if (s.size() != t.size())
			return false;
		sort(s.begin(), s.end());
		sort(t.begin(), t.end());
		if (s!=t)
		{
			return false;
		}
		else
		{
			return true;
		}
	}

5）思路四： 官方思路

bool isAnagram5(string s, string t) {
		if (s.length() != t.length()) {
			return false;
		}
		vector<int> table(26, 0);
		for (auto& ch : s) {
			table[ch - 'a']++;
		}
		for (auto& ch : t) {
			table[ch - 'a']--;
			if (table[ch - 'a'] < 0) {
				return false;
			}
		}
		return true;
	}

❤ 2021-9-11 ❤

4、有效的字母异位词

1）题目： 简单

2）思路一： 12ms 对 S 和 T 两个字符串排序，排完序后两者是否相同。

bool isAnagram3(string s, string t) {
		if (s.size() != t.size())
			return false;
		sort(s.begin(), s.end());
		sort(t.begin(), t.end());
		if (s!=t)
		{
			return false;
		}
		else
		{
			return true;
		}
	}

3)思路二： （12ms 还耗内存）创建两个哈希表，分别存储 S 和 T 的字符，键是字符，键值是字符出现次数，再比较两个哈希表是否相同。

	bool isAnagram(string s, string t) {
		map<char, int> str1;
		map<char, int> str2;
		int length = s.size();
		if (s.size() != t.size())
			return false;
		for (int i = 0; i < length; i++)
		{
			++str1[s[i]] ;
			++str2[t[i]];
		}
		if (str1!=str2)
			return false;
		return true;
	}

4）思路三： 4ms 官方思路，官方就是官方啊

bool isAnagram4(string s, string t) {
		if (s.size() != t.size())
			return false;
		vector<int> table(26, 0);
		int length = s.size();
		for (int i = 0; i < length; i++)
		{
			++table[s[i] - 'a'];
		}
		for (int i = 0; i < length; i++)
		{
			table[t[i] - 'a']--;
			if (table[t[i] - 'a'] < 0)
				return false;
		}
		return true;

	}

❤ 2021-9-12 ❤

5、验证回文串

1）题目： 简单

2）思路一： 把字符串中的大小写字母，数字，存在一个数组中，如果是大写字母，转化成小写字母。最后遍历看第 i 个和第 length-i-1是否相等。 4ms

bool isPalindrome(string s) {
		vector<char> table;
		for (auto& ch : s) {
			if ((ch > 64 && ch < 91) || (ch > 96 && ch < 123) || (ch > 47 && ch < 58)) {
				if (ch > 64 && ch < 91)
					ch += 32;
				table.push_back(ch);
			}
		}
		int length = table.size();
		for (int i = 0; i < length/2; i++)
		{
			if(table[i] != table[length - 1 - i])
				return false;
		}
		return true;
	}

2）思路二： 在思路一的基础上，把只有小写字母和数字的数组倒序，看与原数组是否相等。 0ms

bool isPalindrome2(string s) {
		string table;
		for (auto& ch : s) {
			if ((ch > 64 && ch < 91) || (ch > 96 && ch < 123) || (ch > 47 && ch < 58)) {
				if (ch > 64 && ch < 91)
					ch += 32;
				table.push_back(ch);
			}
		}
		string table2 = table;
		reverse(table2.begin(), table2.end());
		if (table2 != table)
			return false;
		return true;

	}

❤ 2021-9-13 ❤

6、字符串转换整数

1）题目： 主要是考虑溢出


2）思路： 常规思路，缺啥补啥，调试了好久。感觉自己的代码太繁琐了，官方是自动机算法，没看懂。而且自动机算法还没有ifelse的时间短。
有符号数注意 *n ------- ** result = result * 10 + (s[i] - ‘0’)*n; **

int myAtoi(string s) {
		long result=0;
		int length = s.size();
		int n = 1;
		int length2 = 0;
		for (int i = 0; i < length; i++)
		{
			if (s[i]==' ' && length2==0)
			{
				continue;
			}
			else if ( s[i] == '-' && length2 == 0) {
				++length2;
				n = -1;
			}
			else if (s[i] == '+'  && length2 == 0) {
				++length2;
				n = 1;
			}
			else if (s[i] > 47 && s[i] < 58) {
				++length2;
				if (n == 1 && result > (INT_MAX - (s[i] - '0') * n) / 10) return INT_MAX;
				else if (n == -1 && result < (INT_MIN - (s[i] - '0') * n) / 10) return INT_MIN;
				result = result * 10 + (s[i] - '0')*n;
			}
			else {
				break;
			}
			
		}
	
		return result;	
	}

❤ 2021-9-14 ❤

7、实现strStr（）

1）题目：

2)思路一： 双指针，遍历字符串，如果找到相同的，flag标志位置1，j++，如果后面的不相同了，标志位flag再变回0, j 也变回0，同时要注意 i 也要变回 flag置1 时的 i 的下一位，即 i 变成 i-j+1; 由于for循环后面有i++，所以此处 i = i - j ;
但是这种思路太耗时了，要一千多毫秒。o(╥﹏╥)o

int strStr(string haystack, string needle) {
		if (haystack.size() < needle.size()) 
			return -1;
		if (needle == "")
			return 0;
		//双指针
		int  i,j = 0;
		int flag = 0;
		int length = haystack.size();
		int length2 = needle.size();
		for (i = 0; i < length && j<length2; i++)
		{
			if (haystack[i] != needle[j]) {
				if (flag) {
					i = i - j ;
					j = 0;
				}
				continue;
			}
			else
			{
				flag = 1;
				j++;
			}
		}
		if (flag == 1 && j == length2) {
			return i - j;  
		}
		else
		{
			return -1;
		}
	}

3）思路二： 来看一下官方的KMP思路.。好难啊o(╥﹏╥)o，！！
来放几个链接，方便后续观看。
官方解法
KMP算法讲解

class Solution {
public:
    int strStr(string haystack, string needle) {
        int n = haystack.size(), m = needle.size();
        if (m == 0) {
            return 0;
        }
        vector<int> pi(m);
        for (int i = 1, j = 0; i < m; i++) {
            while (j > 0 && needle[i] != needle[j]) {
                j = pi[j - 1];
            }
            if (needle[i] == needle[j]) {
                j++;
            }
            pi[i] = j;
        }
        for (int i = 0, j = 0; i < n; i++) {
            while (j > 0 && haystack[i] != needle[j]) {
                j = pi[j - 1];
            }
            if (haystack[i] == needle[j]) {
                j++;
            }
            if (j == m) {
                return i - m + 1;
            }
        }
        return -1;
    }
};

❤2021-9-22❤

8、外观数组

哎呀！由于这样这样那样那样的原因都好久不刷题了，赶紧快点捡起来。

1）题目：

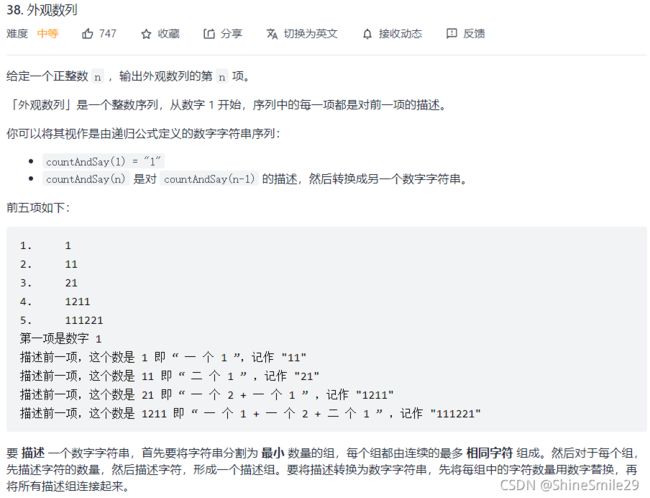
看一眼，又是一道我不会解的题。o(╥﹏╥)o。看答案吧。
2）思路： 外观数列

string countAndSay(int n) {
		if (n == 1) {
			return "1";
		}
		string res = "1";
		for (int i = 1; i < n; i++)
		{
			int number = 0;//记录出现次数
			char curentFirstStr = res[0];//当前字符设置为结果中的第一个字符
			string curentStr = "";//存放临时结果
			for (char ch : res) {
				if (ch == curentFirstStr) {
					number += 1;
				}
				else
				{
					//如果不等，即出现新字符
					//把原来的字符个数和字符推入临时结果
					curentStr.append(to_string(number));
					curentStr.push_back(curentFirstStr);

					//更改当前值和出现次数
					curentFirstStr = ch;
					number = 1;
				}
			}
			//最后一组相同的数存入临时结果
			curentStr.append(to_string(number));
			curentStr.push_back(curentFirstStr);
			res = curentStr;

		}
		return res;
	}

❤2021-9-23❤

9、最长公共前缀

1）题目： 简单

2）思路一： 纵向扫描——从前往后遍历所有字符串的每一列，比较相同列上的字符是否相同，如果相同则继续对下一列进行比较，如果不相同则当前列不再属于公共前缀，当前列之前的部分为最长公共前缀。

string longestCommonPrefix(vector<string>& strs) {
		int length=strs.size();
		int number = 0;
		while (number < strs[0].size())
		{
			for (int i = 0; i < length; i++)
			{
				if (strs[i][number] != strs[0][number]) {
					if (!number)
						return "";
					else
					{
						return string(strs[0],0,number);
					}
				}
			}
			number++;
		}
		return  string(strs[0], 0, number);
	}

3）思路二：分治法
把字符串数组成两段，左半段得到一个最长公共前缀left，右半段的到一个最长公共前缀right。 left与righ的最长公共前缀就是整个数组的公共前缀。

//分治法  8ms
	string longestCommonPrefix(vector<string>& strs) {
		if (!strs.size())
			return "";
		else
		{
			return longestCommonPrefix4(strs, 0, strs.size() - 1);
		}
	}
	//分治法子函数一
	string longestCommonPrefix4(const vector<string>& strs, int start, int end) {
		if (start == end)
			return strs[start];
		else
		{
			int mid = (start + end) / 2;
			string left = longestCommonPrefix4(strs, start, mid);
			string right = longestCommonPrefix4(strs, mid+1, end);
			return CommonPrefix(left, right);
		}
	}
	//分治法子函数二
	string CommonPrefix(string left, string right) {
		int length = min(left.size(), right.size());
		for (int i = 0; i < length; i++)
		{
			if (left[i] != right[i])
				return string(left, 0, i);
		}
		return string(left, 0, length);
	}

链表

1、删除链表中节点

1）题目：

2）思路： 链表知识不熟练，看看答案学习一下

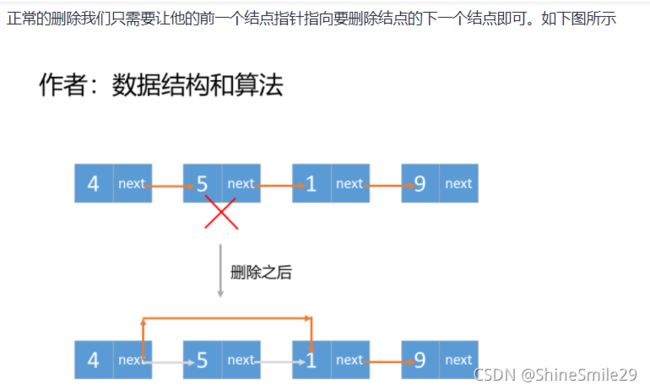
但是由于此链表是单向链表 ，不是双向链表 ，我们没办法知道要删除节点的前一个节点。
换一种思路：把要删除结点的下一个结点值赋给要删除的结点，然后删除下一个结点即可，因为题中说了，删除的结点是非末尾结点。

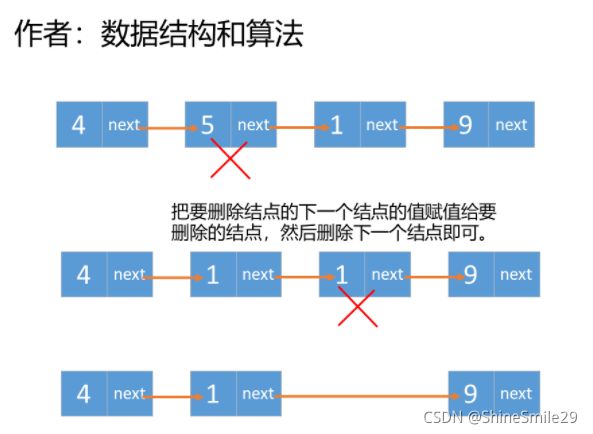
class Solution {
public:
	void deleteNode(ListNode* node) {
		//把要删除节点的下一个节点的值赋值给要删除节点
		node->val = node->next->val;
		//删除下一个节点
		node->next = node->next->next;
	}
};

2、删除链表的第N个节点

1）题目： 又是学习官方答案的一天

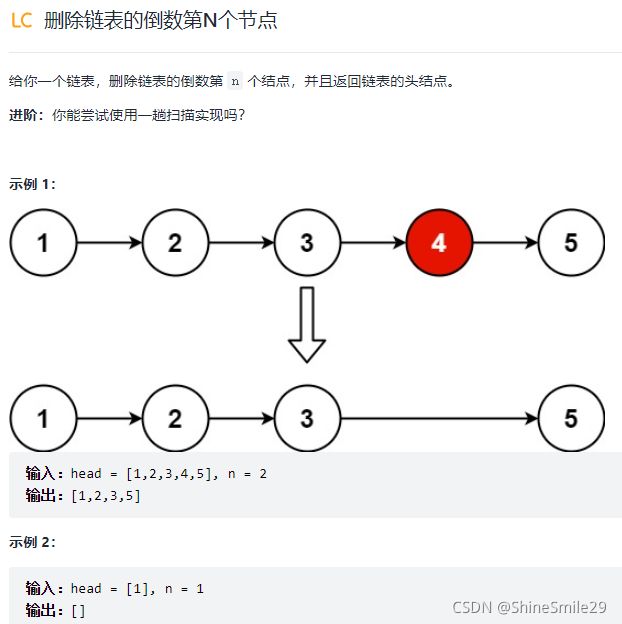
2）思路一： 要找倒数第N个节点，首先要求链表的长度。
然后让要删除节点的前一个节点 pre 的指针指向要删除节点的下一个节点 next。

注意： 本题中要删除节点Y，就要知道节点Y的前驱节点X，并将X的指针指向Y的后继节点。但是，头结点不存在前驱节点，要特殊考虑。因此，为了简便计算，可以在头结点之前插入一个哑节点。这样就可以避免头结点的特殊情况。最后，还要记得把哑结点删除。

//先求一下链表的长度
	int getLength(ListNode* head) {
		int length = 0;
		while (head!=nullptr)
		{
			head = head->next;
			length++;
		}
		return length;
	}
	ListNode* removeNthFromEnd(ListNode* head, int n) {
		//在头结点之前添加一个哑结点
		//当链表只有头结点时，不存在前一个节点
		ListNode* demo = new ListNode(0, head);
		ListNode* ptr = demo;
		//这个长度是原来链表的长度，不加哑结点之前的
		int length = getLength(head);
		//找到要删除节点的前一个节点
		for (int i = 1; i < length-n+1; i++)
		{
			ptr = ptr->next;
		}
		//把要删除节点的前一个节点指向要删除节点的后一个节点
		ptr->next = ptr->next->next;
		//[1] 1不通过。。。最后要把哑结点删除
		ListNode* last = demo->next;
		delete demo;
		return last;
		
	}

3）思路二： 栈，利用栈先入后出的性质，链表的倒数第N个节点就是栈的第N个。
首先把链表中的值依次压入栈；
栈要加入头文件

#include

//方法二：栈
	ListNode* removeNthFromEnd2(ListNode* head, int n) {
		//在头结点之前添加一个哑结点
		//当链表只有头结点时，不存在前一个节点
		ListNode* demo = new ListNode(0, head);
		ListNode* ptr = demo;
		//创建栈
		stack<ListNode*> stk;
		while (ptr!=nullptr)
		{
			//把链表中的值依次压入栈
			stk.push(ptr);
			ptr = ptr->next;
		}
		//栈有先入后出的特性，把倒数第n个元素推出栈
		for (int i = 0; i < n; i++)
		{
			stk.pop();
		}
		
		//栈顶元素就是要删除元素的前驱元素
		ListNode* prev = stk.top();
		prev->next = prev->next->next;
		//删除哑结点
		ListNode* ans = demo->next;
		delete demo;
		return ans;
		
	}

4）思路三：快慢指针（实在是高）

//方法三：快慢指针 8ms
	ListNode* removeNthFromEnd3(ListNode* head, int n) {
		//在头结点之前添加一个哑结点
		//当链表只有头结点时，不存在前一个节点
		ListNode* demo = new ListNode(0, head);
		ListNode* first = head;
		ListNode* second = demo;
		//first超前second N 个节点
		for (int i = 0; i < n; i++)
		{
			first = first->next;
		}
		//当first到达链表末尾时，second正好位于要删除节点的前驱节点
		while (first!=nullptr)
		{
			first = first->next;
			second = second->next;
		}
		second->next = second->next->next;
		ListNode* ans = demo->next;
		return ans;
	}

❤2021-9-28❤

3、反转链表

1）题目：

2）思路一： 把链表 {1,2,3,4,5} 存入数组S {1,2,3,4,5} 。再把数组转化成链表。因为链表先存入的会在尾部，就相当于把原来的链表倒序了。

//方法一
	ListNode* reverseList(ListNode* head) {
		if (head == nullptr || head->next == nullptr)
			return head;
		//把链表转成数组
		vector<int> s = creatVector(head);
		int n = s.size();
		ListNode* new_head = new ListNode;
		//再把数组转成链表
		creatList(new_head, n, s);
		return new_head->next;
	}
	//把链表转化成数组
	vector<int> creatVector(ListNode* head) {
		vector<int> s;
		ListNode* ptr = head;
		while (ptr!=nullptr)
		{
			s.push_back(ptr->val);
			ptr = ptr->next;
		}
		return s;
	}
	//把数组转化成链表
	void creatList(ListNode* head, int n,vector<int> s) {
		ListNode* ptr = head;
		ptr->next = nullptr;
		for (int i = 0; i < n; i++)
		{
			ListNode* p = new ListNode;
			p->val = s[i];
			p->next = ptr->next;
			ptr->next = p;
		}
	}

3）思路二： 双指针反转链表

	//双指针，也可以叫迭代
	ListNode* reverseList2(ListNode* head) {
		if (head == nullptr || head->next == nullptr)
			return head;
		//创建两个指针
		//一个指向链表头部
		ListNode* pre = head;
		//一个为空
		ListNode* cur = nullptr;
		while (pre!=nullptr)
		{
			//每次让 pre 的 next 指向 cur ，实现一次局部反转
			//局部反转完成之后，pre 和 cur 同时往前移动一个位置
			//循环上述过程，直至 pre 到达链表尾部
			ListNode* t = pre->next;
			pre->next = cur;
			cur = pre;
			pre = t;
		}
		return cur;
	}

4）思路三：栈

ListNode* reverseList3(ListNode* head) {
		ListNode* ptr = head;
		//注意栈的定义
		stack<ListNode*> stc;
		//入栈
		while (ptr!=nullptr)
		{
			stc.push(ptr);
			ptr = ptr->next;
		}
		if (stc.empty())
			return nullptr;
		ListNode* nul= new ListNode;
		ListNode* demo = nul;
		//出栈
		while (!stc.empty())
		{
			//ListNode* node = stc.top();
			//注意此处是demo.next=stc.top而不是demo=stc.top。
			//如果是后者只会返回一个值
			demo->next = stc.top();
			demo = demo->next;
			stc.pop();
		}
		demo->next = nullptr;
		return nul->next;	
	}

❤2021-9-29❤

4、合并两个升序链表

1）题目：简单

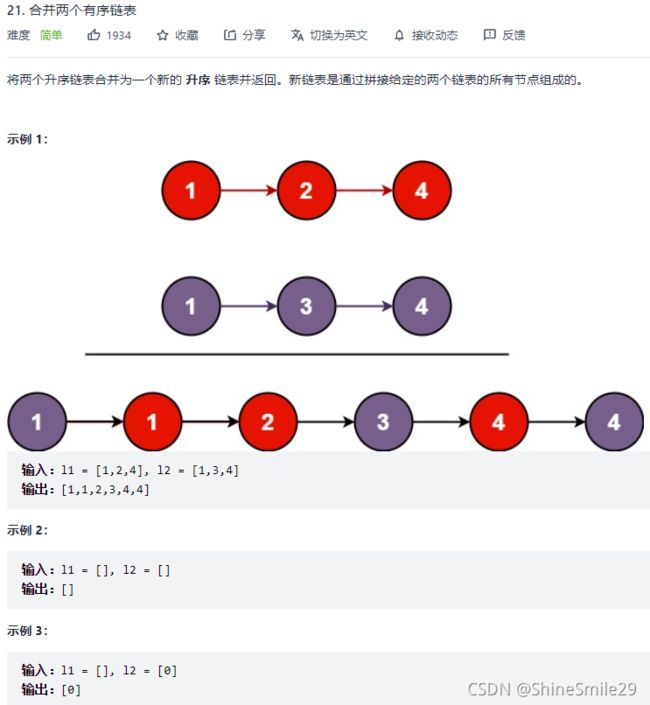
2）思路一： 因为链表是升序的，我们只需要遍历每个链表的头，比较一下哪个小就把哪个链表的头拿出来放到新的链表中，一直这样循环，直到有一个链表为空，然后我们再把另一个不为空的链表挂到新的链表中。

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
		ListNode* head = new ListNode;//存储结果的空链表
		//开始就是没有定义扫描指针，结果总是不对
		ListNode* ptr = head;//扫描指针
		if (l1 == nullptr)
			return l2;
		else if ( l2 == nullptr)
			return l1;
		else {
			while (l1 != nullptr && l2 != nullptr)
			{
				if (l1->val < l2->val) {
					ptr->next = l1;
					l1 = l1->next;
				}
				else
				{
					ptr->next = l2;
					l2 = l2->next;
				}
				ptr = ptr->next;
			}
			//不要忘记把没有遍历完的链表加在后面
			ptr->next = l1 == nullptr ? l2 : l1;
		}
		return head->next;
	
	}

3）思路二： 递归
在思路一的基础上改成递归

ListNode* mergeTwoLists2(ListNode* l1, ListNode* l2) {
		if (l1 == nullptr)
			return l2;
		else if (l2 == nullptr)
			return l1;
		else {
				if (l1->val < l2->val) {
					l1->next = mergeTwoLists2(l1->next, l2);
					return l1;
				}
				else
				{
					l2->next = mergeTwoLists2(l1, l2->next);
					return l2;
				}

			}               
	}

❤2021-10-2❤

5、回文链表

1）题目

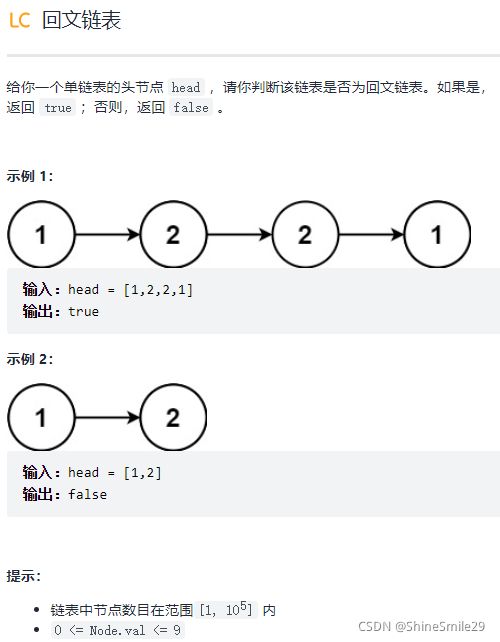
2）思路一：栈
把链表所有值压入栈，然后再依次出栈，出栈过程中比较是否与链表中的值相同。

//时间240ms 太长了
	bool isPalindrome(ListNode* head) {
		ListNode* ptr = head;
		//注意 stack stc; 栈中存入的是int类型的值
		//	   stack stc;栈中存入的是指针
		stack<int> stc;
		if (head == nullptr)
			return false;
		int length = 0;
		//入栈
		while (ptr!=nullptr)
		{
			stc.push(ptr->val);
			ptr = ptr->next;
			length++;
		}
		//出栈
		length = length / 2;
		while (length)
		{
			int p = stc.top();//反回栈顶元素
			if ( p != head->val)
				return false;
			else
			{
				stc.pop();//弹出栈顶元素，不会反回值
				head = head->next;
				length--;
			}
		}
		return true;
	}

3）思路二：快慢指针
定义两个指针 fast 和 slow ，开始时两个指针都指向链表头，fast每次移动两步，即 fast = fast->next->next；slow每次移动一步，即 slow = slow->next；这样当fast移动到 终点 时，slow刚好移动到 中点 。
然后，把链表后半部分反转（后半部分的表头是slow或slow->next(如果fast最后不为空说明链表长度是奇数个,此时后半部分的表头就是slow->next)），fast指针回到表头。
最后比较fast和slow指针指向的值是否相同。

//快慢指针118ms
	bool isPalindrome2(ListNode* head) {
		ListNode* fast = head;
		ListNode* slow = head;
		//fast每次移动两步，slow每次移动一步，即fast移动的距离是slow的2倍
		//所以当fast到终点时slow位于中点
		while (fast!=nullptr&&fast->next!=nullptr)
		{
			fast = fast->next->next;
			slow = slow->next;
		}
		//如果fast最后不为空说明链表长度是奇数个
		//这时要从slow的下一位开始反转
		if (fast!= nullptr) {
			slow = slow->next;
		}
		//fast重新指向表头
		fast = head;
		//把后半部分链表反转
		slow = reverseList(slow);
		while (slow!=nullptr)
		{
			if (slow->val != fast->val)
				return false;
			else
			{
				slow = slow->next;
				fast = fast->next;
			}
		}
		return true;
	}
	//反转链表
	ListNode* reverseList(ListNode* head) {
		if (head == nullptr || head->next == nullptr)
			return head;
		ListNode* ptr = reverseList(head->next);
		head->next->next = head;
		head->next = nullptr;
		return ptr;
	}

6、环形链表

1）题目

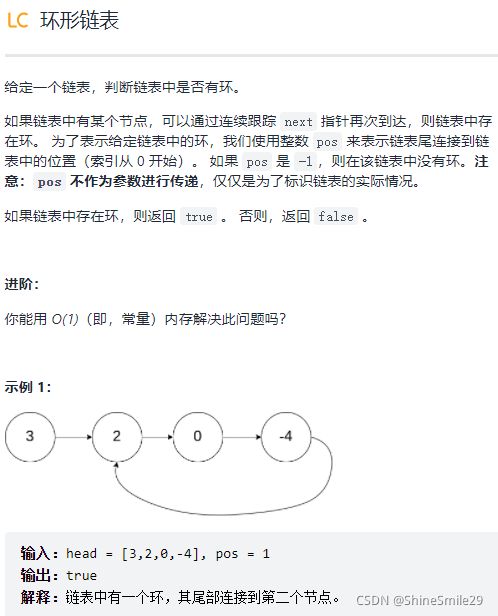
2）思路一：快慢指针。
定义两个指针slow和fast，同上一题，如果fast和slow相遇，说明是环状链表；反之则不是。

	//8ms
	bool hasCycle(ListNode* head) {
		if (head == nullptr)
			return false;
		//快慢指针
		//如果他们相遇就是环装链表
		ListNode* fast = head;
		ListNode* slow = head;
		while (fast != nullptr && fast->next != nullptr) {
			fast = fast->next->next;
			slow = slow->next;
			//把上下交换了一下位置就好了
			if (fast == slow)
				return true;

		}
		return false;
	}

3）思路二：哈希表
把链表 节点 存入哈希表，键是节点，键值是出现次数，某个节点的出现次数大于一就是环型链表。

//24ms
	//把链表的节点存入哈希表，如果有相同的值说明有环，否则没环
	bool hasCycle2(ListNode* head) {
		//创建哈希表键是节点，键值是出现次数
		map<ListNode*,int> app;
		while (head !=nullptr && head->next!=nullptr)
		{
			if (app.count(head))
				return true;
			else
			{
				app[head] = 1;
				head = head->next;
			}
		}
		return false;
	}

4）思路三：删除加递归
一个链表从头节点开始一个个删除，所谓删除就是让他的next指针指向他自己。如果没有环，从头结点一个个删除，最后肯定会删完，如果是环形的head=head->next。

//递归删除
	bool hasCycle3(ListNode* head) {
		//结束条件
		if (head == nullptr || head->next == nullptr)
			return false;
		//上下颠倒会报错
		if (head == head->next)
			return true;
		ListNode* ptr = head->next;
		//让head的下一个节点等于他本身，就删除了它本身
		head->next = head;
		//从head的下一个节点开始递归
		return hasCycle3(ptr);

	}

❤2021-10-8❤

树

1、二叉树的最大深度

1）题目：

2）基础知识回顾：
树的表示：

 struct TreeNode {
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode() : val(0), left(nullptr), right(nullptr) {}
     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 };

使用数组递归创建二叉树：

TreeNode* BuildTree(vector<int>& vec , int index) {
		TreeNode* root = nullptr;
		if (index < vec.size() && vec[index] != NULL) {
			root = new TreeNode(vec[index]);
			root->left = BuildTree(vec, 2 * index + 1);
			root->right = BuildTree(vec, 2 * index + 2);

		}
		return root;
	}

3）思路：
二叉树的高度 H 为左子树的最大高度 L 与右子树的最大高度 R 两者之间的最大值加1。即 H = MAX { L , R } + 1。
而左子树与右子树的最大高度又可以通过此种方法求得，因此可以用递归的方法求解二叉树的高度。

	int maxDepth(TreeNode* root) {
		int HL, HR, MaxH;
		if (root != nullptr) {
			HL = maxDepth(root->left);
			HR = maxDepth(root->right);
			MaxH = HL > HR ? HL : HR;
			return MaxH + 1;
		}
		else
		{           
			return 0;
		}
	}

❤2021-10-9❤

2、验证二叉搜索树

1）题目

2）思路一：递归
如果该二叉树的左子树不为空，那左子树上所有节点的值都小于它的根节点；如果右子树不为空，那右子树上所有节点的值都大于它的根节点。
我首先想到的思路是递归，代码如下：

bool isValidBST(TreeNode* root) {
		//递归终止条件
		if (root == nullptr)
			return true;
		if (root->left != nullptr && root->val <= root->left->val || root->right != nullptr && root->val >= root->right->val) {
			return false;
		}
		//递归
		return isValidBST(root->left) && isValidBST(root->right);
	}

但是这种思路测试时有部分值并没有通过，看答案才知道没有考虑越界的的问题。评论区一位大佬的解释很清晰。

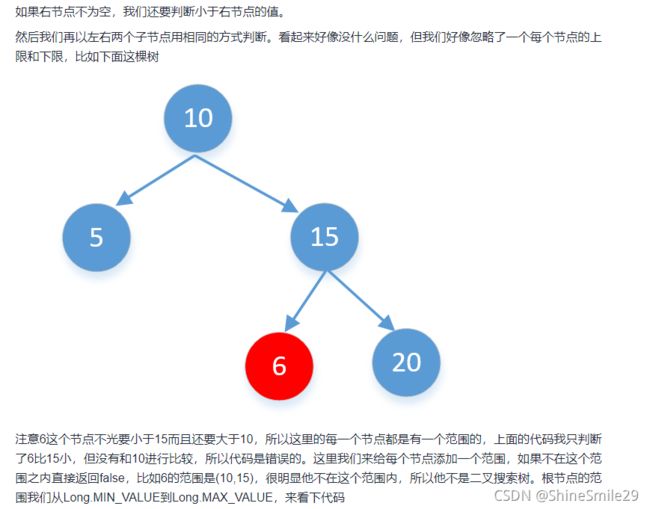
	//递归
	bool isValidBST(TreeNode* root) {
		return isValidBST(root,LONG_MIN,LONG_MAX);
	}
	
	bool isValidBST(TreeNode* root, long minVal, long maxVal) {
		if (root == nullptr)
			return true;
		//每个节点如果超过这个范围，直接返回false
		if (root->val >= maxVal || root->val <= minVal)
			return false;
		//这里再分别以左右两个子节点分别判断，
		//左子树范围的最小值是minVal，最大值是当前节点的值，也就是root的值，因为左子树的值要比当前节点小
		//右子数范围的最大值是maxVal，最小值是当前节点的值，也就是root的值，因为右子树的值要比当前节点大
		return isValidBST(root->left, minVal, root->val) && isValidBST(root->right, root->val, maxVal);
	}

3）思路二：中序遍历递归
中序遍历的顺序是，左子树——根节点——右子树，而我们又知道二叉搜索树左子树的值 < 根节点的值 < 右子树的值 。所以可以利用中序遍历的这一特点，判断当前节点的值是否大于前一节点的值。故要设置一个全局变量存储前一节点的值。

	//存放前一节点，全局变量
	TreeNode* pre;
	//中序遍历加递归
	bool isValidBST2(TreeNode* root) {
		if (root == nullptr)
			return true;
		//左子树
		if (!isValidBST(root->left))
			return false;
		//当前节点，当前节点要大于前一节点
		if (pre != nullptr && pre->val >= root->val)
			return false;
		pre = root;
		//访问右子树
		if (!isValidBST(root->right))
			return false;
		return true;
	}

3、对称二叉树

1）题目：

2）思路一：开始想的思路是把二叉树转换成数组，然后比较数组是否对称相等。但是测试发现这种不能出里二叉树位置为空的情况。如{ 1,2,2,2,NULL,2 }；
不过此处中序遍历非递归模式值得学习。

vector<int> ConvertTtoV(TreeNode* root) {
		TreeNode* T = root;
		vector<int> vec;
		stack<TreeNode*> stc;
		while (!stc.empty())
		{
			while (T) {
				stc.push(T);
				T = T->left;
			}
			if (!stc.empty()) {
				T = stc.top();
				vec.push_back(T->val);
				stc.pop();
				T = T->right;
			}
		}
		return vec;	
	}

3）思路二：官方答案——通过递归，同步移动两个指针。
看二叉树是否对称，比较左右子树是否对称；
首先左子树的根节点等于右子树；
其次，左子树的左子树与右子树的右子树镜像对称；
左子树的右子树与右子树的左子树镜像对称；
左子树和右子树的左右子树同时满足上面三条规则。

//方案二递归
	//判断二叉树是否对称 ，比较左右子树的根节点
	//首先他们根节点值相同
	//左子树的左子树与右子树的右子树镜像对称
	//左子树的右子树与右子树的左子树镜像对称
	bool isSymmetric2(TreeNode* root) {
		return isSymmetric2(root->left, root->right);
	}
	bool isSymmetric2 (TreeNode* l, TreeNode* r) {
		//叶子节点
		if (!l && !r)
			return true;
		//左右子树只有一个有子节点，一定不对称
		if (!l || !r)
			return false;
		return l->val==r->val && isSymmetric2(l->left, r->right) && isSymmetric2(l->right, r->left);
	}

4、二叉树的层序遍历

1）题目

2）思路：
先回顾一下层序遍历的过程：

	vector<vector<int>> levelOrder(TreeNode* root) {
		queue<TreeNode*> q;//将每一层的元素入栈
		vector<vector<int>> vec;//当数值从队列弹出时，放入数组中
		if (!root)
			return vec;
		q.push(root);
		while (!q.empty())
		{
			int length = q.size();
			vec.push_back(vector<int>());//先创建一层的空间
			for (int i = 0; i < length; i++)
			{
				//从队列中取出一个元素
				//因为队列中的元素会被弹出，所以要存在一个新的临时变量中
				auto node = q.front();
				q.pop();
				vec.back().push_back(node->val);
				if (node->left)
					q.push(node->left);
				if (node->right)
					q.push(node->right);
			}
		}
		return vec;
	}

5、将有序数组转化为二叉搜索树

1）题目：

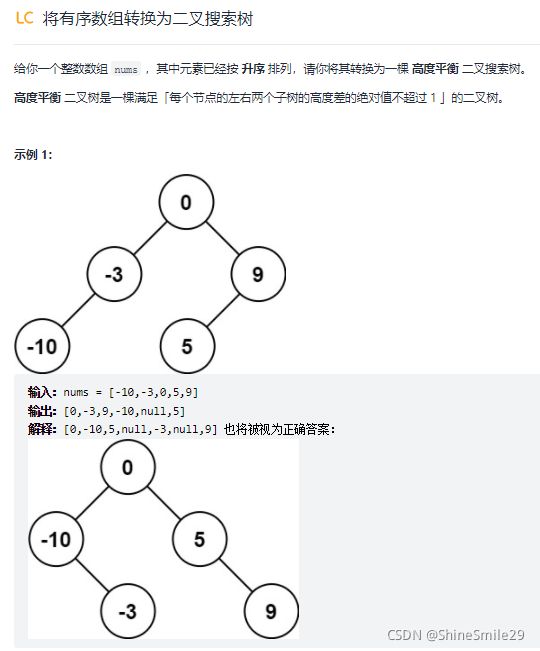
2）思路：注意题目中的两个关键词 “升序” 和 “高度平衡二叉树”
首先可以想到，数组中间的值（vec[mid]）一定是根节点，此时mid把数组分成了左右两部分，
左半部分是左子树的值，右半部分是右子树的值。
左半部分再找中间值作为左子树的根节点，右半部分同理，以此类推用递归。

TreeNode* sortedArrayToBST(vector<int>& nums) {
		//中序遍历，把中间的节点作为根节点插入
		return Insert(nums,0,nums.size()-1);
	}
	TreeNode* Insert(vector<int>& nums, int left, int right) {
		if (left > right)
			return nullptr;
		int mid = (left + right) / 2;
		TreeNode* root = new TreeNode(nums[mid]);
		root->left = Insert(nums, left, mid - 1);
		root->right = Insert(nums, mid + 1, right);
		return root;
	}

排序和搜索

1、合并两个有序数组

1）题目：

2）思路一：这个题首先想到的思路就是，把 nums2 ,插入到 nums1 后面，然后用 c++ 的 sort 函数。

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
		for (int i = m; i < m+n; i++)
		{
			nums1[i] = nums2[i - m];
		}
		sort(nums1.begin(), nums1.end());
	}

但是感觉这种思路有点投机取巧的意思。于是又想了下面的双指针思路。
3）思路二：定义指针 top（i） 和 bottom（j），top指向nums1开头，bottom指向nums2开头；
比较两只大小，把小值放入新的数组，并且小值指针向右移。
注意： 当一个指针已到末尾时，但是另一个指针可能还没有到末尾，此时要把另一个数组中的剩余元素插入到新数组后面。
刚开始没有注意到这点一直报错。

void merge2(vector<int>& nums1, int m, vector<int>& nums2, int n) {
		vector<int>nums;
		int i = 0, j = 0;
		while (i<m || j<n)
		{
			if (j==n) {
				nums.push_back(nums1[i]);
				i++;
			}
			else if (i == m) {
				nums.push_back(nums2[j]);
				j++;
			}
			else if (nums1[i] <= nums2[j]) {
				nums.push_back(nums1[i]);
				i++;
			}
			else
			{
				nums.push_back(nums2[j]);
				j++;
			}
		}
		for (int i = 0; i < m+n; i++)
		{
			nums1[i] = nums[i];
		}
	}

2、第一个错误的版本

1）题目：

2）思路一：首先想到的是二分法 mid=（left+right）/ 2 ；但是越界报错。后来看答案发现把改成 mid=left+（right-left）/2 就对了，具体为什么不是很清楚。

int firstBadVersion(int n) {
		int start = 1, end = n;
		while (start < end) {
			int mid = start + (end - start) / 2;
			//是false的话要检测它的下一位
			//第一个错误版本在他的右侧，缩小左边界。
			if (!isBadVersion(mid))
				start = mid + 1;
			//是true的话要检测当前位置
			//第一个错误版本在他的左侧，缩小右边界。
			else
				end = mid;
		}
		return start;
	
	}

动态规划

1、爬楼梯

1）题目

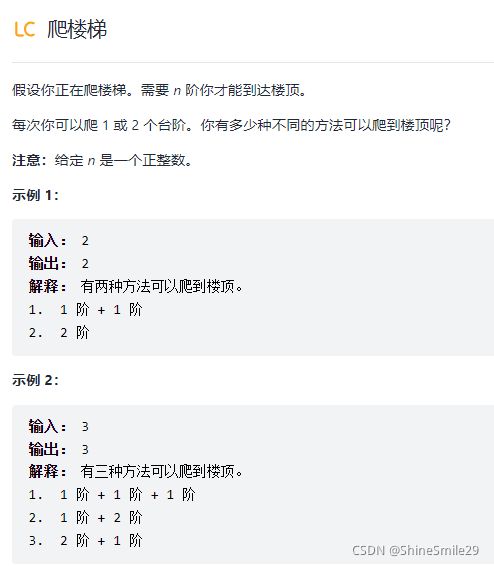
2）思路一：先列举几个找找规律
n = 1 ——1种
n = 2 ——2种（1+1、2）
n = 3 ——3种（1+1+1、2+1、1+2）
n = 4 ——2种（1+1+1+1、2+2、2+1+1、1+2+1、1+1+2）
惊喜的发现这不就是斐波那契数列吗（开始的时候n=4算错了，导致浪费了好多时间想，唉！不认真太耽误事了）
于是有了最原始的斐波那契数列代码

//低效斐波那契 
int climbStairs2(int n) {
		if (n <= 1)
			return 1;
		else
		{
			return climbStairs2(n - 1) + climbStairs2(n - 2);
		}	
	}

但是很不幸超时了。
将递归改成迭代，因为递归有好多重复的代码，导致时间过长。

//优化斐波那契
	int climbStairs(int n) {
		int last, next, answer;
		if (n <= 1)
			return 1;
		last = next = 1;
		for (int i = 2; i <= n; i++)
		{
			answer = last + next;
			last = next;
			next = answer;
		}
		return answer;
	}

2、买股票的最佳时期

1）题目：

2）思路： 开始一看这不是跟之前做过的一个题一样吗。后来经师兄提醒才发现原来不一样啊。
上一道题不限买卖次数，但是本道题只能买买一次。对比一下上一道题

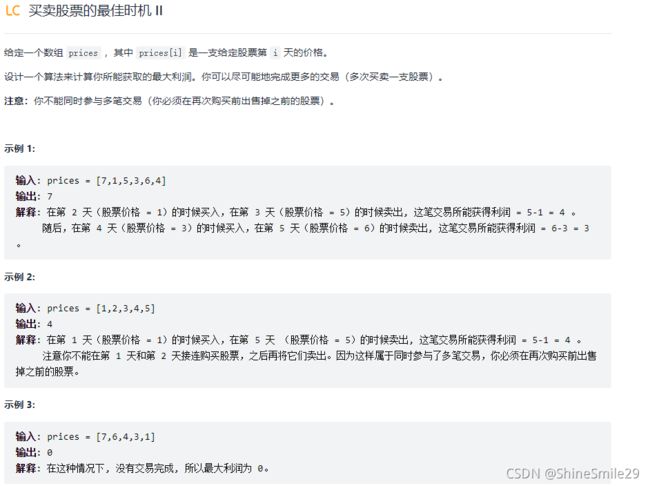
动态规划的四步
1、确定状态
2、找到转移公式
3、确定初始条件和边界条件
4、计算结果
dp[i][0] 表示第i天手里没有股票的最大收益：可能等于第i-1天手里没有股票的收益dp[i-1][0] 或者为第i -1天有股票第i天卖了股票的收益dp[i-1][1]+price[i]，即
dp[i][0] =max（dp[i-1][0]，dp[i-1][1]+price[i]）
dp[i][1]表示第i天手里有股票的最大收益：可能等于第i-1天手里没有股票的收益也就是0（因为一共只能买买一次）再减去今天买股票花的钱，以前就是 -price，或者或者为第i -1天有股票的收益dp[i-1][1]；即
dp[i][1] =max（dp[i-1][1]，-price[i]）
以上是递推公式。

	//动态规划
	int maxProfit(vector<int>& prices) {
		//注意注意——这个题要求一星期只买卖一次，与上一题不同
		int length = prices.size();
		int(*dp)[2];//定义一个二位数组；
		dp = new int[length][2];
		//边界条件
		dp[0][0] = 0;
		dp[0][1] = -prices[0];
		//递推公式
		for (int i = 1; i < length; i++)
		{
			dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);//dp[i - 1][1]肯定是负的
			dp[i][1] = max(dp[i - 1][1], -prices[i]);
		}
		//最后一题没股票收益最大
		return dp[length - 1][0];
	}

3）思路二： 除了动态规划的思路还可以用双指针，一个指针指向最小值，另一个指针循环遍历。

//双指针
	int maxProfit2 (vector<int>& prices) {
		int length = prices.size();
		int min = prices[0];
		int result = 0;
		for (int i = 0; i < length; i++)
		{
			if (prices[i] < min)
				min = prices[i];
			int num = prices[i] - min;
			if (num > result)
				result = num;
		}
		return result;

	}

3、最大子序列和

1）题目：

2）思路一：

• dp[i] 表示前 i+1 个元素最大的子序列和（元素从0开始计数）
• 如果要计算dp[i] ，就要知道 dp[i-1]是大于0，还是小于0， （ 注意： 不是判断nums[i] 是否大于0）
• 如果dp[i-1] > 0, dp[i] = nums[i] + dp[i-1] ; 如果 dp[i-1] < 0 ,dp[i] = nums[i]; 所以转移公式是 dp[i] = nums[i] + max ( dp[i-1] , 0);
• 边界条件判断，当i等于0的时候，也就是前1个元素，他能构成的最大和也就是他自己，所以
  dp[0] = num[0];

int maxSubArray2(vector<int>& nums) {
		vector<int> dp;
		int length = nums.size();
		dp.push_back(nums[0]);
		int maxnum = dp[0];
		//opt.push_back(max(nums[0], nums[1]));
		for (int i = 1; i < length; i++)
		{
			dp.push_back(nums[i] + max(dp[i - 1], 0));
			//dp[i] = nums[i] + max(dp[i - 1], 0);
			maxnum = max(dp[i], maxnum);
		}
		return maxnum;
	}

3）思路二： 在一的基础上进行优化
因为在计算 dp[i] 时只用到了 dp[i-1] ，前面的都没有用到，所以为了避免造成空间的浪费，用一个临时变量存储 dp[i-1] 就好。

int maxSubArray2(vector<int>& nums) {
		int length = nums.size();
		int number = nums[0];
		int maxnum =number;
		for (int i = 1; i < length; i++)
		{
			number = nums[i] + max(number, 0)
			maxnum = max(number , maxnum);
		}
		return maxnum;
	}

4、打家劫舍（求数组不相邻元素的最大和）

1）题目：

2）思路一：递归——超出时间限制

• dp[i] 表示 i 位置之前不相邻元素的和的最大值
• 如果选了第 i 个元素，dp[i] = dp[i-2] +nums[i];
• 如果不选第 i 个元素，dp[i] = dp[i-1];
• 边界条件 dp[0] = nums[0]; dp[1] = max(nums[0] , nums[1]);

//超出时间限制
	int rob(vector<int>& nums) {
		return rob(nums, nums.size() - 1);
	}
	int rob(vector<int>& nums,int len) {
		if (len == 0)
			return nums[0];
		else if (len == 1)
			return max(nums[0], nums[1]);
		else
		{
			int a = rob(nums, len - 2) + nums[len];
			int b = rob(nums, len - 1);
			return max(a, b);
		}
	}

3）思路二：非递归

int rob(vector<int>& nums) {
		vector <int>sum;
		int length = nums.size();
        if(length==1)
        	return nums[0];
		sum.push_back(nums[0]);
		sum.push_back(max(nums[0], nums[1]));
		for (int i = 2; i < length; i++)
		{
			int a = sum[i - 2] + nums[i];
			int b = sum[i - 1];
			sum.push_back(max(a,b));
		}
		return sum[length - 1];
	}

❤2021-11-05❤

设计问题

1、打乱数组

1）题目：

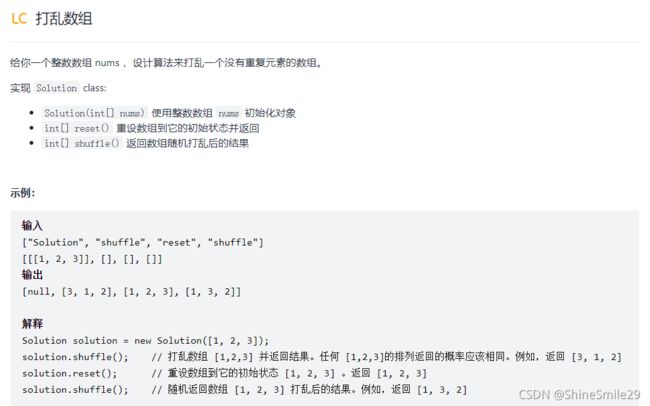
2）思路：此题考查 “洗牌算法”
数组倒序遍历，摄当前位置是 i ，产生一个 [0,i] 之间的随机数 p,让 a[i] 和 a[p] 交换位置。

产生一定范围随机数的通用表示公式
要取得[a,b)的随机整数，使用(rand() % (b-a))+ a;
要取得[a,b]的随机整数，使用(rand() % (b-a+1))+ a;
要取得(a,b]的随机整数，使用(rand() % (b-a))+ a + 1;
通用公式:a + rand() % n；其中的a是起始值，n是整数的范围。
要取得a到b之间的随机整数，另一种表示：a + (int)b * rand() / (RAND_MAX + 1)。
要取得0～1之间的浮点数，可以使用rand() / double(RAND_MAX)

此处还要注意 不要直接对原数组进行操作，要把原数组拷贝一份再操作。

class Solution {
	vector<int> vec;
public:
	Solution(vector<int>& nums) {
		vec = nums;
	}

	vector<int> reset() {
		return vec;
	}

	vector<int> shuffle() {
		auto a = vec;
		int length = a.size();
		//要取得[a,b]的随机整数，使用(rand() % (b-a+1))+ a;
		for (int i = length-1; i  ; i--)
		{
			int p = rand() % (i+1);//随机生成一个0—i的数
			int temp = a[p];
			a[p] = a[i];
			a[i] = temp;
			//也行，就是时间长点
			//swap(a[p],a[i]); 
		}
		return a;
	}
};

2、最小栈

1）题目：

2）思路：使用辅助栈解决
每在原栈中放入一个值就在辅助栈中放入目前新栈中的最小值。辅助栈的栈顶元素永远是原栈中所有元素的最小值。

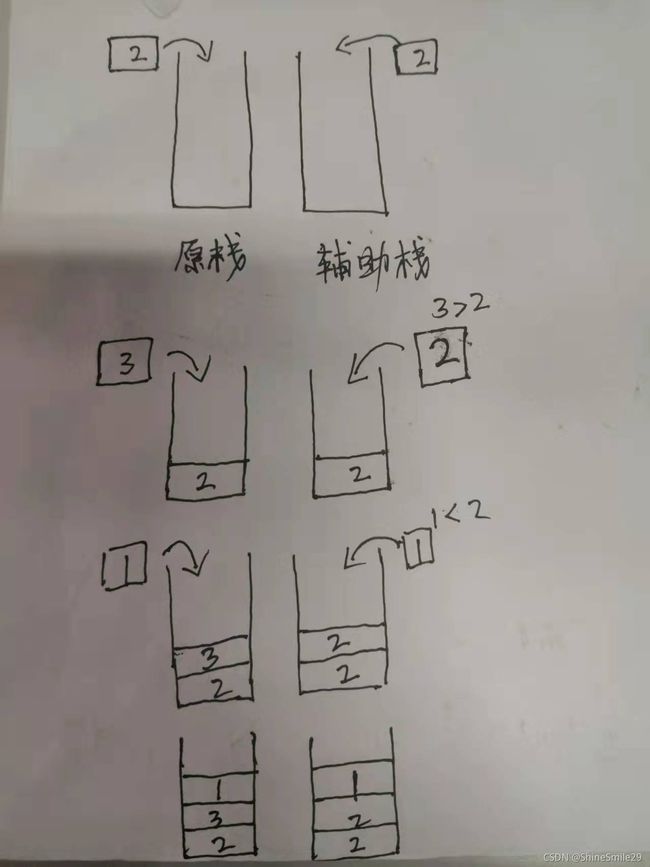
注意： 辅助栈中要先压入int型整数的最大值

class MinStack {
	stack<int> stc;
	//利用辅助栈，stc每压入一个元素，min_stc也压入一个最小的
	stack<int> min_stc;
public:
	MinStack() {
		min_stc.push(INT_MAX);
	}

	void push(int val) {
		stc.push(val);
		min_stc.push(min(val, min_stc.top()));
	}

	void pop() {
		stc.pop();
		min_stc.pop();

	}

	int top() {
		return stc.top();
	}

	int getMin() {
		return min_stc.top();
	}
};

数学

1、Fizz Buzz

1)题目：

2）思路：此题比较简单，直接用 if - else if - else 就可以

vector<string> fizzBuzz(int n) {
		vector<string>  result ;
		//result.push_back("0");
		for (int i = 1; i < n+1; i++)
		{
			if (i % 3 == 0 && i % 5 == 0) {
				result.push_back("FizzBuzz");
			}
			else if (i % 3 == 0 ) {
				result.push_back("Fizz");
			}
			else if (i % 5 == 0) {
				result.push_back("Buzz");
			}
			else
			{
				result.push_back(to_string(i));
			}
		}
		return result;
	}

2、计算质数

1）题目：

2）思路一：暴力算法——超时

int countPrimes2(int n) {
		if (n <3)
			return 0;
		int num = 1 ; //2是质数 
		//除了2的偶数肯定不是质数，只判断奇数
		for (int i = 3 ; i < n; i+=2)
		{
			if (i > 10) {
				if (i % 3 == 0 || i % 5 == 0 || i % 7 == 0)
					continue;
			}
			for (int j = 3; j < i+1 ; j+=2) {
				if (i % j == 0 && i != j)
					break;
				if (i == j)
					num++;
			}
			
		}
		return num;
	}

3）官方枚举法

	bool counttest(int x) {
		for (int i = 2;i * i <= x ; i++)
		{
			if (x % i == 0)
				return false;
		}
		return true;
	}
	int countPrimes3(int n) {
		if (n < 3)
			return 0;
		int num = 1;
		for (int i = 3; i < n; i+=2)
		{
			num += counttest(i);
		}
		return num;
	}

4）思路三：埃氏筛（重点！重点！重点！）

如果 x 是质数，那么大于 x 的 x 的倍数 2x,3x,… 一定不是质数。

我们设isPrime[i] 表示数 i 是不是质数，如果是质数则为 1，否则为 0。从小到大遍历每个数，如果这个数为质数，则将其所有的倍数都标记为合数（除了该质数本身），即 0，这样在运行结束的时候我们即能知道质数的个数。

对于一个质数 x，如果按上文说的我们从 2x开始标记其实是冗余的，应该直接从 x*x 开始标记，因为 2x,3x,… 这些数一定在 x 之前就被其他数的倍数标记过了.

//埃氏筛
	int countPrimes(int n) {
		//是质数，第二位是1，反之为0;先初始化都为1
		vector<int> isPrimes(n,1);
		int num = 0;
		for (int i = 2; i < n; i++)
		{
			if (isPrimes[i]) {
				num += 1;
				//isPrimes[i] 的倍数就不是质数
				//long long：是64位的整型，取值范围为-2^63 ~ (2^63 - 1)。
				if ((long long)i * i < n) {
					//因为i*i之前的 2*i  3*i 已经在i*i之前就被标记过了
					for (int j = i*i; j < n; j+=i)
					{
						isPrimes[j] = 0;
					}
				}
			}

		}
		return num;
	}

3、3的幂

1）题目：

2）思路一：分两步
首先，n 是 3 的倍数 ；然后 n 被 3 整除后还是 3 的倍数。直到 n = 1 则 n 就是 3 的幂。

class Solution {
public:
    bool isPowerOfThree(int n) {
        if (n == 0)
			return false;
        while ( n % 3 == 0)
		{
			n = n / 3;
		}
		if(n==1)
			return true;
		else
		{
			return false;
		}
    }
};

3）思路二：判断是否是 最大3的幂 的约数

class Solution {
public:
    bool isPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }
};

4、罗马数字转整数

1）题目：

2）思路：此题主要是处理6种特殊情况。

class Solution {
public:
    int romanToInt(string s) {
		int length = s.size();
		int n = 0;
		//保存前一个值,注意应该是 char 类型 ，不应该是string类型
		char pre_s = NULL;
		for (int  i = 0; i < length; i++)
		{
			switch (s[i]) {
				case 'I':n += 1;
					break;
				case 'V':
					if (pre_s == 'I')
						n += 3;
					else
					{
						n += 5;
					}
					break;
				case 'X':
					if (pre_s == 'I')
						n += 8;
					else
					{
						n += 10;
					}
					break;
				case 'L':
					if (pre_s == 'X')
						n += 30;
					else
					{
						n += 50;
					}
					break;
				case 'C':
					if (pre_s == 'X')
						n += 80;
					else
					{
						n += 100;
					}
					break;
				case 'D':
					if (pre_s == 'C')
						n += 300;
					else
					{
						n += 500;
					}
					break;
				case 'M':
					if (pre_s == 'C')
						n += 800;
					else
					{
						n += 1000;
					}
					break;
			}
			pre_s = s[i];
		}
		return n;
	}
};

其他

1、位 1 的个数

1）题目：

2）思路：
首先回顾一下c++中的位运算：

任何数与 1 进行 & 运算 ，最终结果都是它本身。所以让 n的末尾与 1 进行 与（&）运算，再循环右移；

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int num = 0;
		for (int i = 0; i < 32; i++)
		{
			if (((n >> i) & 1) == 1)
				num++;
		}
		return num;
    }
};

2、汉明距离

1）题目：

2）思路：先让两个数进行异或（^）运算，找出出现不同数的位置。再利用上一题中位1的个数，就可以求出汉明距离了

class Solution {
public:
    int hammingDistance(int x, int y) {
        //进行异或运算；
		int n = x ^ y;
		//计算位1的个数
		int num = 0;
		for (int i = 0; i < 32; i++)
		{
			if (((n >> i) & 1) == 1)
				num++;
		}
		return num;
    }
};

3、颠倒二进制位

1）题目：

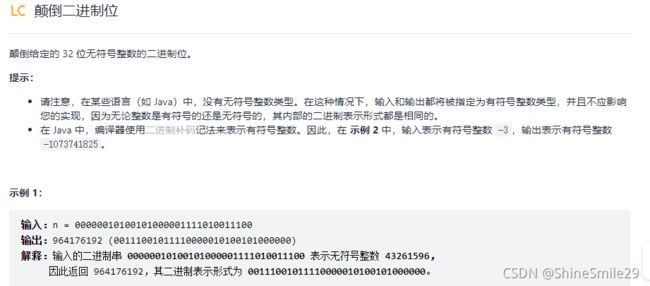
2）思路一：
每次循环的时候把n的最后一位数字（二进制的）截取掉，放到一个新的数字中的末尾。每次循环时新的数字左移一位。n 右移一位。

class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
    // pre 存放的是 n 的末尾数字
    // p 存的是反转结果
        uint32_t pre ,p = 0;
		for (int i = 0; i < 32; i++)
		{
			pre = (n >> i) & 1;
			p = p << 1;
			p += pre;
		}
		return p;
    }
};

3）思路二：分治法（重点！ 重点！重点！）
取出所有奇数位和偶数位；
将奇数位移到偶数位上，偶数位移到奇数位上

class Solution {
private:
	//2个数交换奇偶位
	const uint32_t M1 = 0x55555555;		//0101 0101 0101 0101 0101 0101 0101 0101
	//4个数（2位一组）交换奇偶位
	const uint32_t M2 = 0x33333333;		//0011 0011 0011 0011 0011 0011 0011 0011
	//8个数（4位一组）交换奇偶位
	const uint32_t M4 = 0x0f0f0f0f;		//0000 1111 0000 1111 0000 1111 0000 1111
	//16个数（8 位一组）交换奇偶位
	const uint32_t M8 = 0x00ff00ff;		//0000 0000 1111 1111 0000 0000 1111 1111

public:

	//重点：分治法
	uint32_t reverseBits(uint32_t n) {
		n = n >> 1 & M1 | (n & M1) << 1;
		n = n >> 2 & M2 | (n & M2) << 2;
		n = n >> 4 & M4 | (n & M4) << 4;
		n = n >> 8 & M8 | (n & M8) << 8;
		return n >> 16 | n << 16;

	}
};

4、杨辉三角形

1）题目：

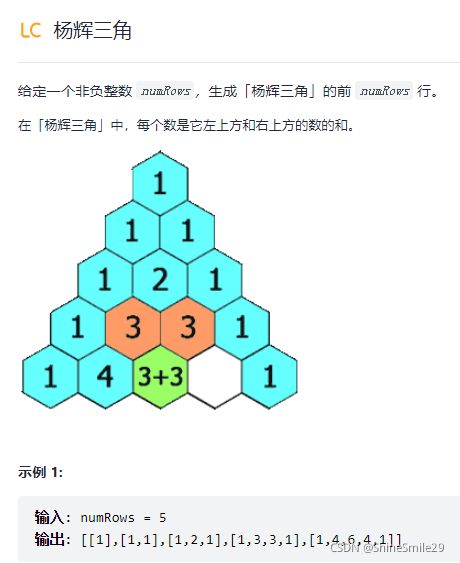
2）思路：
明显可以知道 a [ i ] [ 0 ] = a [ i ][ i ] = 1；a [ i ][ j ] = a [ i -1 ][ j ] + a [ i -1 ][ j -1 ]；
此处要注意记住用 vector 表示二进制数组的方法。

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector < vector<int>> array(numRows);//行
        //可以把创建列的循环放在下一个循环里，
		//这里这样写是为了逻辑清晰
		for (int i = 0; i < numRows; i++)
		{
			array[i].resize(i + 1);//列
		}
		for (int i = 0; i < numRows; i++)
		{
			array[i][0] = 1;
			for (int j = 1; j < i ; j++) {
				array[i][j] = array[i - 1][j - 1] + array[i - 1][j];
			}
			array[i][i] = 1;
		}
		return array;
    }
};

5、有效括号

1)题目：

2）思路：此题没有想到用栈解决，看了答案。

bool isValid(string s) {
		int length = s.size();
		//遍历字符，遇到左括号，把对应的右括号压入栈
		stack<char> stc;
		for (int i = 0; i < length; i++)
		{
			switch (s[i])
			{
			case '(':
				stc.push(')');
				break;
			case '{':
				stc.push('}');
				break;
			case '[':
				stc.push(']');
				break;
			default:
				if (stc.empty()) {
					return false;
				}
				else
				{
					if (stc.top() == s[i]) {
						stc.pop();
						break;
					}
					else
					{
						return false;
					}
				}
				
			}
		}
		//最后如果栈为空，说明是完全匹配，是有效的括号，否则如果栈不为空，说明不完全匹配，不是有效的括号。
		if (stc.empty()) {
			return true;
		}
		else
		{
			return false;
		}
	}

6、缺失数字

1）题目：

2）思路一：哈希表
第一个参数存的是 [0,n] 之间的值；第二个参数表示，如果nums数组中如果有这个值就位 1 ，没有就为 0；但是这种思路时间太长了，要76ms

//76ms
	int missingNumber(vector<int>& nums) {
		int length = nums.size();
		map<int, int> p;
		for (int i = 0; i < length; i++)
		{
			p[nums[i]] = 1;
		}
		for (int i = 0; i <= length; i++)
		{
			if (p[i] == 0)
				return i;
		}
		return 0;
	}

3）思路二：排序
对数组进行排序，在循环遍历排查。时间相应缩短但还是很长。28ms

int missingNumber(vector<int>& nums) {
		sort(nums.begin(), nums.end());
		int length = nums.size();
		for (int i = 0; i < length; i++)
		{
			if (nums[i] != i)
				return i;
		}
		return length;
	}

4)思路三：想不出更简单的办法了，于是看了官方答案。12ms

//求和 12ms
	int missingNumber(vector<int>& nums) {
		int length = nums.size();
		int sum = (length + 1) * (0 + length) / 2;//n/2(a1+an)
		for (int i = 0; i < length; i++)
		{
			sum -= nums[i];
		}
		return sum;
	}

5）思路四：位运算

//位运算 16ms
	int missingNumber(vector<int>& nums) {
		int length = nums.size();
		int res = 0;
		for (int i = 0; i < length; i++)
		{
			res ^= nums[i] ^ (i + 1);
		}
		return res;
	}

总结

❤ 2021-11-19 ❤
如今，初级算法已经刷完，下周就要开始刷中级算法了。
通过这一时间的做题还是有些进步的。还记得刚开始我都搞不懂如何在力扣里面提交结果，如何在VS里面写程序调试；最开始一道题也解不出来，甚至有时候都不明白题目的意思，只能每次都看答案。把答案看明白了，自己再动手敲代码。就这样一遍一遍，每日一题。总算是把初级算法刷完了。
通过这次刷题，学到了c++中的 vector 向量，map ,list ,stack等数据结构，也学到了KMP算法，分治算法，动态规划…还有好多都记不起来了。以后还要好好复习。一边刷中级算法，一遍回顾初级的。